4. 逐步簡化，不斷剔除“劣勢策略”

博弈通常是一場復雜的競爭。對于參與者而言，這場競爭中往往存在多種策略方案。到底應該選擇哪一種策略呢？這是一個考驗智慧的問題。如果博弈中存在一個顯而易見的優勢策略，那么參與者在做決策時就會簡單得多，只須直接選擇優勢策略即可。

不過，在大多數博弈中，并沒有明顯的優勢策略，甚至不存在優勢策略。遇到這樣的復雜情況，我們只能逐步找到并剔除劣勢策略，從而簡化決策過程，找到相對優勢的策略。這是一個循序漸進的過程。我們首先需要排除最劣勢的策略，然后排除相對劣勢的策略，直到只剩下相對最優策略為止。

什么是劣勢策略呢？在一場博弈中，如果存在兩種或兩種以上的策略，其中一種策略比其他任何一種都差，如收益最少、效用最低等，那么這種策略就是劣勢策略。我們要首先排除最劣勢的策略，逐漸縮小決策的范圍。

在博弈中，使用策略的規則是，如果我們擁有一個優勢策略，那么我們會首選優勢策略，敵方也會這樣做。如果我們擁有一個劣勢策略，我們要剔除劣勢策略，敵方也會如此。如果我們只有兩個策略，其中一個是優勢策略，另一個就是劣勢策略。

規避劣勢策略常常運用于一方擁有至少三個選擇的復雜博弈中。我們需要經過復雜的計算過程，才能選出劣勢策略。

以下是一個商業活動中的投資案例，正好說明了計算劣勢策略的過程。

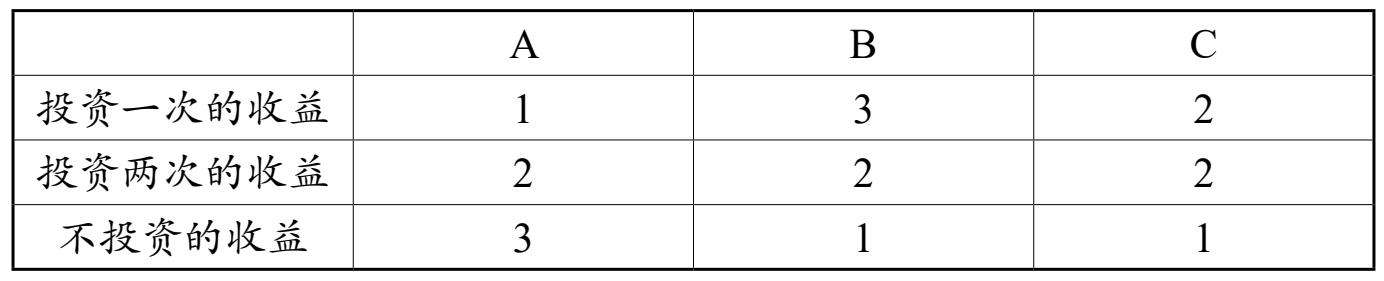
假設在博弈中，有A、B、C三位投資人，A投資一次、投資兩次和不投資的收益分別是1、2、3，則A有三種策略。其中，“投資一次”的收益最少，是劣勢策略，應該剔除。

而對于B而言，投資一次、投資兩次和不投資的收益分別是3、2、1。由此可見，B也有三種策略，其中“不投資”的收益最少，是劣勢策略，應予剔除。

對于C而言，投資一次、投資兩次和不投資的收益分別為2、2、1，則C也有三種策略，其中“不投資”的收益最少，是劣勢策略，應該剔除。

在這個例子中，A和B兩位參與者，如果三方的利益不能共享，那么他們各自既有劣勢策略，也有優勢策略。各自尋找最優的策略，可以得到最大的收益。這是比較簡單的博弈，很容易做出對自己有利的決策。

但對于C而言，如果三者的利益不能共享，則沒有最優策略。C只能在剔除劣勢策略之后，在剩下的兩種策略中選擇，即“投資一次”或“投資兩次”。這兩者的收益相等，均為2，但付出不同，因此我們可以再次剔除投資兩次這一相對劣勢的策略，那么最終剩下的就是投資一次這一相對優勢的策略。

如果A、B、C三位參與者的利益可以共享，則有三種不同的策略。這三種策略當中，沒有最優策略，只有劣勢策略。因此，應當剔除劣勢策略。

三方投資一次的共同收益是6，投資兩次的共同收益也是6，不投資的共同收益是5，因此“不投資”這一劣勢策略應該剔除。然后進一步剔除投資兩次這一付出較多的劣勢策略。