- 數(shù)學(xué)原來可以這樣學(xué):思維養(yǎng)成篇
- (英)喬·博勒
- 5809字
- 2025-08-12 16:19:47
數(shù)學(xué)家們到底在研究什么?
費(fèi)馬大定理是由偉大的法國數(shù)學(xué)家皮埃爾·德·費(fèi)馬于17世紀(jì)30年代提出的一個(gè)定理。幾個(gè)世紀(jì)以來,無數(shù)數(shù)學(xué)家付出了巨大努力想要證實(shí)或證偽這一定理,使得這個(gè)定理被稱為“世界上最難被證實(shí)或證偽的數(shù)學(xué)問題”之一。在那個(gè)年代,費(fèi)馬因?yàn)樘岢鲞^不少數(shù)字之間的奇妙關(guān)系而聞名于世,費(fèi)馬大定理就是其中之一。
在公元前4—5世紀(jì),畢達(dá)哥拉斯發(fā)現(xiàn)a2+b2=c2(譯者注:即畢達(dá)哥拉斯定理),而費(fèi)馬進(jìn)一步推論,對(duì)于方程an+bn=cn,如果n>2,則方程沒有整數(shù)解。比如,方程a3+b3=c3中的a、b、c不可能都是整數(shù)。老師通常在教三角形的時(shí)候介紹這個(gè)定理:所有直角三角形,兩條直角邊的平方和(a2+b2)等于斜邊的平方(c2)。
基于畢達(dá)哥拉斯定理,我們可以看出當(dāng)直角三角形的兩條邊長(zhǎng)分別為3和4時(shí),斜邊長(zhǎng)必定為5。因?yàn)?2+42=52。
根據(jù)畢達(dá)哥拉斯定理中的三個(gè)數(shù)的平方數(shù)(比如4,9,16,25)的關(guān)系,我們可以由兩個(gè)數(shù)的平方數(shù),求得另外一個(gè)數(shù)。
費(fèi)馬受畢達(dá)哥拉斯定理的啟發(fā),想將該定理進(jìn)一步延伸至三次方,研究立方數(shù)中的規(guī)律。他希望能證實(shí)在某些情況下,通過兩個(gè)數(shù)的立方數(shù)能求得第三個(gè)數(shù)的立方數(shù)。但費(fèi)馬發(fā)現(xiàn)驗(yàn)證過程并不像平方數(shù)那么順暢,他總湊不出一個(gè)大小剛好的完全立方數(shù)。和費(fèi)馬猜想最近的結(jié)果如圖所示。
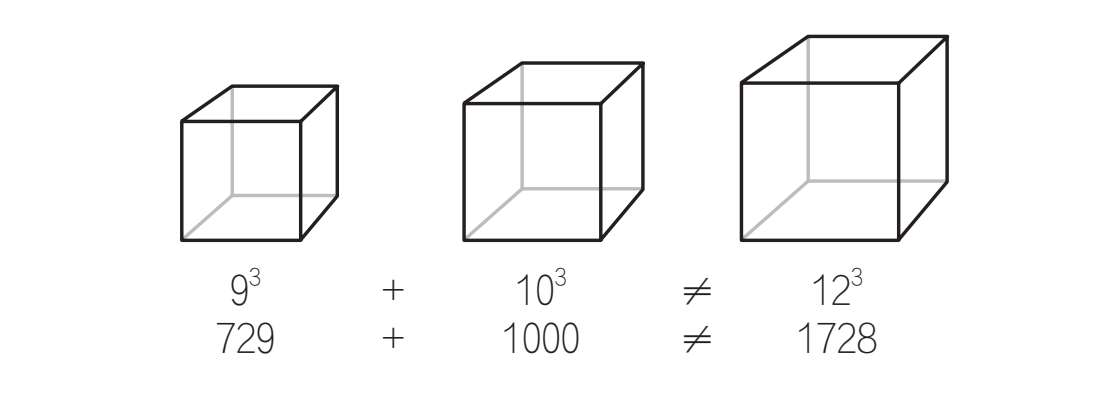
棱長(zhǎng)為9和10的兩個(gè)立方體的體積加起來最接近棱長(zhǎng)為12的立方體的體積,但仍相差了1!
于是,費(fèi)馬進(jìn)一步斷言,世界上的所有數(shù)字都不能滿足a3+b3=c3或4a+b4=c4,甚至,更高次冪的方程也不存在能夠滿足的數(shù)字。
這在數(shù)學(xué)界屬于非常大膽的猜想,因?yàn)樵跀?shù)學(xué)研究中,猜想本身不是證明,即便枚舉成百上千個(gè)數(shù)字作為例子,只要無法窮盡,就不能確切證實(shí)或證偽。畢竟,數(shù)學(xué)就是由能夠經(jīng)受時(shí)間考驗(yàn)的證明建立而成。數(shù)學(xué)證明需要一系列邏輯論證,進(jìn)而得出唯一的、確定的結(jié)果,一旦建立并證實(shí),這些論證將永遠(yuǎn)是正確的。
費(fèi)馬在17世紀(jì)30年代寫下了這個(gè)猜想,卻沒有留下證明,他在稿紙的空白處批注道:“我已經(jīng)有了一套絕妙的論證思路,只是這里位置不夠,寫不下。”此后,這項(xiàng)數(shù)學(xué)難題受到多代偉大數(shù)學(xué)家的關(guān)注,在接下來的350多年歷史長(zhǎng)河中,費(fèi)馬大定理始終沒有得到圓滿證實(shí)或證偽,也因此成為“世紀(jì)數(shù)學(xué)難題”之一。
出乎意料的是,在20世紀(jì)90年代,這一世紀(jì)難題被一位靦腆的英國數(shù)學(xué)家安德魯·懷爾斯證實(shí)。多位傳記作者講述了他的成名逸事,但這項(xiàng)數(shù)學(xué)證明本身卻少有人知道。如果你想看看這個(gè)世紀(jì)難題的解決過程,想了解歷代數(shù)學(xué)家如何不懈追求真理,或是想體驗(yàn)純粹的數(shù)學(xué)之美,都可以去讀讀西蒙·辛格的《費(fèi)馬大定理》一書。辛格在書中描述了這一“人類探索的偉大事跡”,對(duì)數(shù)學(xué)家的工作方式提出了重要見解。
在費(fèi)馬大定理被證實(shí)之前,學(xué)界大多數(shù)人認(rèn)為這一難題無法證明,是無解的。全球各界為此設(shè)立豐厚的獎(jiǎng)金,意在鼓勵(lì)大家繼續(xù)挑戰(zhàn),但一批又一批數(shù)學(xué)研究者努力半生,都無功而返。然而終于有位數(shù)學(xué)家——安德魯·懷爾斯取得了成功。
這位被載入史冊(cè)的數(shù)學(xué)家第一次接觸費(fèi)馬大定理的時(shí)候,還是個(gè)10歲的孩子。他在自己劍橋老家的圖書館里看到了費(fèi)馬大定理。懷爾斯感慨道:“這個(gè)看起來如此簡(jiǎn)單的問題,卻幾個(gè)世紀(jì)都解不出來。我當(dāng)時(shí)只有10歲,但從那一刻起,我就知道我繞不開這道題了,我必須解開。”
多年以后,懷爾斯從劍橋大學(xué)獲得了數(shù)學(xué)博士學(xué)位,成為普林斯頓大學(xué)的一名數(shù)學(xué)系教師。隨著工作的深入,懷爾斯意識(shí)到,自己應(yīng)該把所有精力放在自己兒時(shí)就確定的目標(biāo)——費(fèi)馬大定理上。
于是他放下了手頭的工作,埋首于文獻(xiàn)和最前沿的數(shù)學(xué)技術(shù)當(dāng)中。七年又七年,懷爾斯用不同方法去證明費(fèi)馬大定理,以求解決的最優(yōu)路徑。終于在某天下午,經(jīng)過反復(fù)驗(yàn)證,他高興地跑出來叫喊著妻子的名字,自己終于解出費(fèi)馬大難題了。
1993年,懷爾斯在劍橋大學(xué)內(nèi)的牛頓數(shù)學(xué)科學(xué)研究所公布了他的證明結(jié)果。當(dāng)人們聽到這一消息時(shí),都想來看這350多年懸而未決的問題是如何解決的。當(dāng)天的會(huì)場(chǎng)擠滿了200多名數(shù)學(xué)家,甚至有人偷偷帶來相機(jī)把這激動(dòng)人心的場(chǎng)面記錄下來。
被擋在門外的人則更多,他們寧愿在窗外翹首張望,也不愿錯(cuò)過這一歷史時(shí)刻。懷爾斯用了三節(jié)講座才把他的證明闡述完畢,最后一節(jié)結(jié)束時(shí),會(huì)場(chǎng)響起了雷鳴般的掌聲。
西蒙·辛格也在其中,他形容當(dāng)時(shí)的參會(huì)者都“無比激動(dòng)”,人們一時(shí)間還沒來得及接受,這個(gè)世紀(jì)大難題終于被解決了嗎?數(shù)論學(xué)家和代數(shù)幾何學(xué)家巴里·梅熱事后回顧這次講座,他說:“我從來沒看過這么精彩的演講,我們跟著懷爾斯教授一同感受著思想的跌宕起伏,又見證他在絕境中誕生出的新穎思路。我認(rèn)為這次講座是費(fèi)馬大定理解題史上的點(diǎn)睛之筆。”
在大家都開始相信費(fèi)馬大定理終于得到證明之時(shí),懷爾斯發(fā)現(xiàn)自己的證明有一個(gè)小疏漏,于是,他又開始埋頭鉆研。又經(jīng)過數(shù)月的攻堅(jiān),1994年9月,懷爾斯再次將完整且正確的證明材料公之于眾。
為了證明費(fèi)馬大定理,懷爾斯運(yùn)用了不同的理論和交叉概念,由此建立了全新的數(shù)學(xué)方法和數(shù)量關(guān)系。同樣參與了費(fèi)馬大定理研究的數(shù)學(xué)家肯·里貝特認(rèn)為,這是一次數(shù)學(xué)思想的革新,讓我們?cè)凇安豢赡堋钡某叨茸龀隽送黄菩匝芯俊?/p>
懷爾斯的事跡被反復(fù)講述多遍,從這些故事里,我們能否得到一些提升數(shù)學(xué)教育質(zhì)量的啟示呢?
比如,數(shù)學(xué)家的工作與學(xué)生的課業(yè)有一大明顯區(qū)別,就是數(shù)學(xué)家面對(duì)的是復(fù)雜的問題,涉及橫跨多領(lǐng)域的交叉思想,問題的解決必然是一項(xiàng)長(zhǎng)期而艱巨的任務(wù);但是學(xué)生們面對(duì)的,是剛好能填滿一節(jié)課的簡(jiǎn)單數(shù)學(xué)題,使用單一的公式就能解決,學(xué)生只需要多練練這類題型,就會(huì)熟能生巧。這簡(jiǎn)直就是天與地的差距。
對(duì)年輕人而言,數(shù)學(xué)家攻克難題時(shí)的堅(jiān)持不懈的精神,是非常寶貴的。面對(duì)工作和生活中的困境,如果年輕人能不輕言放棄、屢敗屢戰(zhàn),那他們必然能從困境中獲得成長(zhǎng)。
曾有記者采訪魯特格斯大學(xué)數(shù)學(xué)系教授黛安娜·麥克拉根,記者問道:“作為一名數(shù)學(xué)研究學(xué)者,你遇到的最棘手的事情是什么?”她回答:“證明定理。”隨后記者又問她工作中最享受的事是什么,結(jié)果她還是回答:“證明定理。”也許,數(shù)學(xué)家的工作狀態(tài)聽起來并不具有吸引力,但他們之所以享受反復(fù)演算、反復(fù)修正的過程,是因?yàn)樗麄兡懿粩嗾{(diào)整心態(tài),獲得螺旋式上升的成就感。而學(xué)生們眼中的數(shù)學(xué),是一道道做錯(cuò)就0分的考題,這一次次失敗的感覺讓學(xué)生把厭惡和逆反心理遷移到數(shù)學(xué)學(xué)科本身。這并不能怪學(xué)生,現(xiàn)在的數(shù)學(xué)課堂氛圍,帶來的往往就是挫敗感。
而數(shù)學(xué)研究工作者成功的原因在于他們面對(duì)的不是考試和分?jǐn)?shù),他們不是在“做題”,而是在“解決問題”。這是多年數(shù)學(xué)研究經(jīng)驗(yàn)贈(zèng)予他們的寶貴觀念,我相信這種觀念當(dāng)代學(xué)生也可以習(xí)得。
解決問題是數(shù)學(xué)家的工作核心,也是工程師的工作核心。數(shù)學(xué)工作都始于猜想。英籍匈牙利裔哲學(xué)家、數(shù)學(xué)家伊姆雷·拉卡托斯將數(shù)學(xué)工作描述為“關(guān)于數(shù)量和形狀之間關(guān)系的計(jì)劃性的猜想過程”。
習(xí)慣于傳統(tǒng)數(shù)學(xué)課堂的學(xué)生也許會(huì)詫異,數(shù)學(xué)家怎么這么喜歡去“猜”呢?畢竟在數(shù)學(xué)課堂上,老師可沒鼓勵(lì)過大家猜一個(gè)答案出來。但英國的一項(xiàng)職場(chǎng)調(diào)查顯示,工作中最有用的數(shù)學(xué)方法,竟然就是摸著石頭過河的“估算”。如果讓上傳統(tǒng)數(shù)學(xué)課的孩子進(jìn)行估算的話,他們會(huì)不知所措,所謂正確答案不都是精確且明確的嗎?他們體會(huì)不到估算的意義在哪兒。于是這些學(xué)生做題的方式往往是本末倒置的,他們會(huì)先算出精確的數(shù)字,再把這個(gè)數(shù)字倒推至更模糊的范圍,來表示估算值。這種思維反映了學(xué)生“猜想”意識(shí)的缺失,認(rèn)為數(shù)學(xué)的求真過程是追求精確的數(shù)值,但解決數(shù)學(xué)問題,不斷猜想和證實(shí)才是核心所在。
提出猜想后,接下來就是反復(fù)迭代的驗(yàn)證工作,包括正向推論、尋找反例進(jìn)行驗(yàn)證和修正猜想,再進(jìn)行下一輪驗(yàn)證。驗(yàn)證猜想的過程,是極具探索性和創(chuàng)造性的,有人將科學(xué)研究與藝術(shù)或音樂創(chuàng)作進(jìn)行過類比。英國數(shù)學(xué)家羅賓·威爾遜認(rèn)為,數(shù)學(xué)和音樂“都是創(chuàng)造性的行為。埋頭在數(shù)學(xué)草稿紙里寫寫畫畫,非常像在五線譜里創(chuàng)作著旋律”。基斯·德夫林也認(rèn)為:“數(shù)學(xué)絕不僅僅是在解決數(shù)字問題,也是在解決生活問題。數(shù)學(xué)是在探索我們所處世界的奧妙之處。很多人說‘?dāng)?shù)學(xué)很沉悶’‘?dāng)?shù)學(xué)很死板’,但我不這么認(rèn)為,在我看來,數(shù)學(xué)充滿了創(chuàng)造的活力。”
不管是在數(shù)學(xué)家的傳記還是在數(shù)學(xué)課堂中,由于篇幅等的限制,數(shù)學(xué)工作者所享受的創(chuàng)造性探索過程都被大幅省略或一筆帶過,只給大眾呈現(xiàn)結(jié)果。數(shù)學(xué)家們反復(fù)探索、不斷迭代的過程難以讓學(xué)生在課堂上逐一體驗(yàn)。畢竟學(xué)習(xí)數(shù)學(xué)的目的,就是利用前人總結(jié)出的研究方法,解決更多數(shù)學(xué)問題。前人探索的道路我們不必原封不動(dòng)再走一次,但這種探索的過程仍然有其不可替代的價(jià)值,我不希望它們?cè)诤⒆拥恼n堂中成為被一筆帶過的內(nèi)容。這與匈牙利數(shù)學(xué)家喬治·波利亞的觀點(diǎn)如出一轍:
“在教育階段,老師的教學(xué)內(nèi)容對(duì)學(xué)生的學(xué)習(xí)效果有重大的影響:如果老師按部就班給孩子灌輸數(shù)學(xué)知識(shí)和公式,這樣無疑扼殺了學(xué)生的興趣,阻礙了他們的智力發(fā)展,浪費(fèi)了初識(shí)數(shù)學(xué)時(shí),探索數(shù)學(xué)之美的大好機(jī)會(huì)。要利用各種值得玩味的數(shù)學(xué)題來激發(fā)孩子們的好奇心,讓孩子們用已經(jīng)學(xué)到的知識(shí)來解決這些問題,并引發(fā)思考,這樣,老師的教學(xué)才會(huì)幫助孩子們逐漸建立起獨(dú)立思考的能力。”
數(shù)學(xué)工作的另一大特點(diǎn)就是合作性。在大家的認(rèn)知里,數(shù)學(xué)家就是一群埋頭單干的孤僻天才,其實(shí)不是。英國數(shù)學(xué)教育學(xué)專家萊昂內(nèi)·伯頓曾對(duì)70位數(shù)學(xué)工作者進(jìn)行深度調(diào)研,發(fā)現(xiàn)他們的工作性質(zhì)與大家的刻板印象完全不同。數(shù)學(xué)工作者的研究成果,有超過一半是多人合力而成。這些數(shù)學(xué)家往往更喜歡在有交流的工作中相互碰撞出各種新的解決方案,原因多種多樣:在工作中能相互學(xué)習(xí)、提升工作效率以及分享研究取得突破的喜悅之情。這些合作的理由,也是教育學(xué)家提倡進(jìn)行課堂小組合作的理由。可惜在當(dāng)下,美國課堂還是“靜悄悄”的。
在數(shù)學(xué)家的工作過程中,我們還看到,想讓數(shù)學(xué)重獲生機(jī)、接地氣,就得學(xué)會(huì)提出問題。人物傳記電影《美麗心靈》中,飽受精神分裂困擾的約翰·納什就在數(shù)學(xué)研究和傳奇的心靈旅程中找到了自己的人生答案。
數(shù)學(xué)不只是解決問題。一位代數(shù)拓?fù)鋵W(xué)家彼得·希爾頓說:“運(yùn)算思維能讓問題得到答案,而數(shù)學(xué)思維能從答案中誕生新的問題和研究方向。”這樣的工作需要?jiǎng)?chuàng)造力和獨(dú)創(chuàng)精神。
反觀現(xiàn)在課堂上學(xué)習(xí)的數(shù)學(xué)方法和數(shù)量關(guān)系,都源于“問題”,而學(xué)生卻沒有機(jī)會(huì)接觸到這些問題的由來,只是直接學(xué)習(xí)“答案”,并且從來沒有向這些問題和答案提出疑問。魯本·赫什的話似乎總結(jié)了這種現(xiàn)象:
“當(dāng)今的數(shù)學(xué)教育現(xiàn)狀,均源于把數(shù)學(xué)看作‘答案’而非‘問題’。這是被動(dòng)學(xué)習(xí)數(shù)學(xué)的人才會(huì)犯的錯(cuò)誤。推動(dòng)數(shù)學(xué)發(fā)展的其實(shí)是一個(gè)個(gè)問題,而解決問題、再提出新問題才是數(shù)學(xué)研究的本質(zhì)。如果將數(shù)學(xué)放置在象牙塔中,使其遠(yuǎn)離生活,那么數(shù)學(xué)就是一門死的學(xué)科,毫無發(fā)展的生機(jī)。”
而老師則要給學(xué)生們傳達(dá)一種信息:數(shù)學(xué)與生活和社會(huì)發(fā)展息息相關(guān)。當(dāng)學(xué)生有機(jī)會(huì)在生活中發(fā)問,并把問題延伸到新的學(xué)習(xí)方向,他們才能知道,數(shù)學(xué)是“活著的”,而不是教科書上那些已經(jīng)被數(shù)學(xué)家規(guī)定好的概念、方法和必背考點(diǎn)。當(dāng)老師能為學(xué)生提供他們感興趣的問題,并把問題延伸到新的知識(shí)點(diǎn),學(xué)生就能從中感受到思考的樂趣,提高學(xué)習(xí)自主性,從而自發(fā)學(xué)習(xí)。
比如英國的數(shù)學(xué)課堂,老師為學(xué)生提供相對(duì)開放且議題更大的問題,讓學(xué)生找到自己感興趣的方向并進(jìn)行獨(dú)立探究。比如,設(shè)計(jì)一套建筑方案。在這種學(xué)習(xí)模式下,學(xué)生有機(jī)會(huì)經(jīng)歷從提出問題到獲得答案的思考過程,甚至自發(fā)探索習(xí)得更高年級(jí)的數(shù)學(xué)概念。此外,學(xué)生的作品就是他們的學(xué)習(xí)成果,納入成績(jī)考核范圍。當(dāng)問及學(xué)生們的學(xué)習(xí)感想時(shí),他們的回答不僅是“非常喜歡”或“收獲很多”,讓我印象深刻的是他們?cè)诖诉^程中的“自我效能感”,他們?yōu)樽约旱膶W(xué)習(xí)成果感到自豪。而在傳統(tǒng)的教學(xué)方法中,他們是沒有這種自豪感的。
數(shù)學(xué)家手上還有一個(gè)強(qiáng)大的工具,就是數(shù)學(xué)中的表達(dá)形式,比如符號(hào)、表格、圖表和圖示。在不同場(chǎng)景下精確使用這些表達(dá)形式,已成為他們的日常工作。在這里,我要聊聊數(shù)學(xué)表達(dá)的精確性。精確性已成為數(shù)學(xué)的一大標(biāo)志,但在學(xué)習(xí)過程中,學(xué)生對(duì)這種精確性褒貶不一:對(duì)一些學(xué)生來說,嚴(yán)謹(jǐn)、精確的概念界定、寫法和溝通方式能幫助他們理解和學(xué)習(xí);但對(duì)另一些學(xué)生來說,老師在枯燥乏味的課堂上講的就是這些學(xué)究氣的、死板的概念,所以學(xué)生就在嚴(yán)謹(jǐn)和枯燥之間畫了一個(gè)等號(hào)。
其實(shí)數(shù)學(xué)的精確性和機(jī)械的教學(xué)方法并不一定對(duì)等。嚴(yán)謹(jǐn)?shù)厥褂眯g(shù)語和符號(hào),并不意味著數(shù)學(xué)排斥開放和創(chuàng)造性的探索。相反,正是有了這些明確、精確的語言、符號(hào)和圖表表達(dá)形式,數(shù)學(xué)工作者才得以放開交流和探索這些數(shù)學(xué)思想。
詩人和藝術(shù)家使用的符號(hào)和隱喻常常如脫韁的野馬般恣肆奔放,相比之下,數(shù)學(xué)家是利用精確的表達(dá)方式來揭示生活中的規(guī)律的。基斯·德夫林感嘆道:
“數(shù)學(xué)符號(hào)和音樂符號(hào)一樣,音符組成樂譜,但樂譜并不等同于音樂。當(dāng)樂譜被歌唱家唱出來或被樂隊(duì)奏響,才有了‘音樂’。音樂在演奏中才有了生命;音樂不存在于樂譜上,而在人們的感官里。數(shù)學(xué)符號(hào)與數(shù)學(xué)的關(guān)系也是如此。”
如此看來,數(shù)學(xué)也是一種“表演”,一種科學(xué)的行為藝術(shù),一種詮釋世界奧秘的方式。如果音樂課也像數(shù)學(xué)課那樣進(jìn)行傳統(tǒng)式教育,那上課的情形將會(huì)是這樣的:課堂上,老師要求學(xué)生熟讀紙上的樂譜,在樂譜里打鉤打叉,以學(xué)好音樂之名,反復(fù)打磨樂譜上的音符。可惜,學(xué)生從來沒有機(jī)會(huì)把自己的樂譜演奏出來。這種課似乎不太值得上下去,因?yàn)閷W(xué)生根本體會(huì)不到音樂的本質(zhì)。但在數(shù)學(xué)課堂里,這種荒謬的教學(xué)方法卻沿襲下來。
懂得“演奏”數(shù)學(xué)符號(hào),就能用精妙的表現(xiàn)形式在數(shù)學(xué)的舞臺(tái)上大展拳腳。而學(xué)生也不應(yīng)該成天對(duì)著前人留下的方法死記硬背,他們需要參與數(shù)學(xué)方法的研究過程,在學(xué)習(xí)中實(shí)踐、在生活中解決問題,利用數(shù)學(xué)知識(shí)“演奏”出自己的精彩篇章。如果他們?cè)谡n堂里沒學(xué)會(huì)應(yīng)用數(shù)學(xué),那么在其他領(lǐng)域也會(huì)過得很艱難,即便是為了考試,也很難有好成績(jī)。
傳統(tǒng)教育方式的錯(cuò)誤思想在于,期待學(xué)生寒窗苦讀十幾年,若是在數(shù)學(xué)領(lǐng)域深造的話,自然能接觸到真正的數(shù)學(xué)。誠然,研究生階段的確能接觸到數(shù)學(xué)的實(shí)際應(yīng)用,因?yàn)檎n業(yè)要求他們利用從前學(xué)到的數(shù)學(xué)工具,用創(chuàng)新的方式解決實(shí)際問題。但事實(shí)上,能把數(shù)學(xué)讀到研究生階段的人可謂鳳毛麟角,基礎(chǔ)教育中的大部分學(xué)生早已放棄了數(shù)學(xué)學(xué)習(xí)。
如果一種教育模式要把學(xué)科的精華放在最后,經(jīng)過一番大浪淘沙的尖子生才能嘗到最后的甜頭,那么這種教育模式就是在暴殄天物。如果基礎(chǔ)教育中的學(xué)生能有機(jī)會(huì)用數(shù)學(xué)家的方式進(jìn)行數(shù)學(xué)研究,包括提出問題,做出猜想,驗(yàn)證和完善猜想,從小組討論中碰撞出新的火花,那么這已然達(dá)到了教育的一大重要目標(biāo):讓學(xué)生體驗(yàn)數(shù)學(xué)真正的運(yùn)作方式。除此之外,學(xué)生還有可能享受數(shù)學(xué)思考的過程,學(xué)習(xí)起來也更加高質(zhì)、高效。
- 數(shù)字經(jīng)濟(jì):“數(shù)字中國”頂層規(guī)劃與實(shí)踐路徑
- 粵港澳大灣區(qū)觀察:帶你看清大灣區(qū)八大產(chǎn)業(yè)發(fā)展前景(《21世紀(jì)經(jīng)濟(jì)報(bào)道》深度觀察)
- 魔鬼數(shù)學(xué):大數(shù)據(jù)時(shí)代,數(shù)學(xué)思維的力量
- 數(shù)量經(jīng)濟(jì)研究(2018年/第9卷/第2期)
- 穿透數(shù)據(jù):經(jīng)濟(jì)數(shù)據(jù)理解要點(diǎn)與分析應(yīng)用(職業(yè)教育經(jīng)濟(jì)管理類新形態(tài)系列教材)
- 統(tǒng)計(jì)學(xué)
- 算力:數(shù)字經(jīng)濟(jì)的新引擎
- 數(shù)量經(jīng)濟(jì)研究(2017年/第8卷/第2期)
- 數(shù)量經(jīng)濟(jì)研究(2016年/第7卷/第2期)
- 定性數(shù)據(jù)的統(tǒng)計(jì)分析
- 數(shù)字化與數(shù)字經(jīng)濟(jì)
- 數(shù)學(xué)史講義概要
- 數(shù)量經(jīng)濟(jì)研究(2016年/第7卷/第1期)
- 走向數(shù)字經(jīng)濟(jì)
- 數(shù)量經(jīng)濟(jì)研究(2019年/第10卷/第1期)