無窮大有多大

上一節中我們討論了數字，其中很多數字相當大。盡管這些數字界的巨無霸（例如西薩·本·達希爾要求的麥粒數量）大得超乎想象，但它們依然是有限的，只要有足夠的時間，你總能將它數到最后一位。

但世界上還有一些真正“無窮大”的數字，無論你花多少時間都寫不完。比如說，“所有數字的數量”顯然無窮大，同樣的還有“一條線上所有幾何點的數量”。除了“無窮大”以外，你還能用什么辦法來描述這樣的數字？或者說，我們能不能比較兩個不同的“無窮數”，看看它們誰“更大”？

“所有數字的數量和一條線上所有幾何點的數量，這兩個數到底哪個大？”我們能這樣問嗎？著名數學家格奧爾格·康托爾頭一次認真審視了這些被視作異想天開的問題，他是當之無愧的“無窮數學”奠基者。

要比較“無窮數”的大小，我們首先會遇到一個問題：這些數字我們既無法描述，也無法數清。康托爾提出：我們可以對兩組無窮數進行配對，每個集合里的一個元素分別對應另一個集合里的一個元素，如果最后它們正好一一對應，任何一個集合都沒有多余的元素，那么這兩個數的大小相等；但是，如果兩組無窮數無法一一對應，某個集合中存在無法配對的剩余元素，那么我們可以說，這個集合的無窮數更大，或者更強。

這顯然是最合理的辦法，事實上，要比較無窮大的數字，我們也只有這個辦法；但是，如果你真的打算采用這種辦法，那你得做好大吃一驚的準備。比如說，奇數的數量和偶數的數量都是無窮大，我們先來比較一下這兩個無窮數。當然，出于直覺，你肯定認為這兩個數相等，它們也完全符合我們剛才描述的規律，奇數和偶數可以列成一對一的組合：

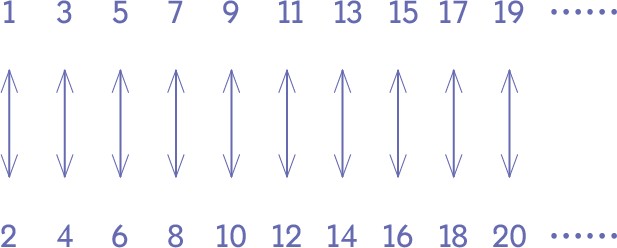
在這張表格中，每個偶數都有一個對應的奇數，反之亦然；因此，奇數的數量和偶數的數量是兩個相等的無窮數。看起來真的非常簡單自然！

不過，請稍等一下。下面兩個數你覺得哪個更大：所有數字的數量（包括奇數和偶數）和偶數的數量？你當然會說，肯定是所有數字的數量更大，因為除了偶數以外，它還包含了奇數。不過這只是你的直覺，要找到準確答案，你得嚴格按照我們上面描述的方法來比較這兩個無窮數。這樣一來，你會驚訝地發現，你的直覺錯了。事實上，所有數字的集合和只有偶數的集合也能做成一張一一對應的表格：

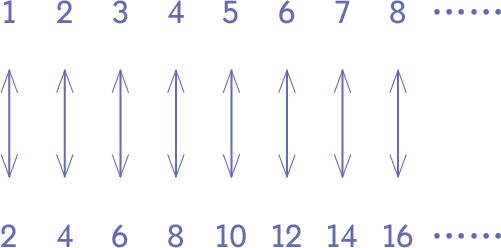
根據無窮數的比較規則，我們只能說，偶數的數量和所有數的數量是兩個相等的無窮數。這聽起來當然很矛盾，因為偶數只是所有數字的一部分，但我們必須記住，這里討論的是無窮數，所以我們只能做好準備，直面它們的古怪特性。

事實上，在無窮數的世界里，部分可能等于整體！這方面最好的例子大概是德國數學家大衛·希爾伯特講的一個故事。據說希爾伯特曾在開講座的時候這樣描述無窮數的矛盾特性：

我們不妨想象一家旅館，它的房間數量是有限的。現在所有房間都住滿了，一位新來的客人想要一個房間。“對不起，”店主回答，“但我們已經客滿了。”接下來，我們再想象一家擁有無窮多個房間的旅館，所有房間同樣住滿了。這家旅館也來了一位想住店的新客人。

“當然可以！”店主熱情地喊道。于是他將原來住在一號房的客人挪到二號房，二號房的客人挪到三號房，三號房的挪到四號房，以此類推……最后新客人住進了剛剛騰出來的一號房。

現在我們繼續想象，一家旅館擁有無窮多個房間，現在來了無窮多個想住店的新客人。

“沒問題，先生們，”店主回答，“稍等一下。”

他讓一號房的客人挪到二號房，二號房的客人挪到四號房，三號房的客人挪到六號房，以此類推……

現在所有奇數號的房間都空了出來，新來的無窮多位客人輕輕松松就安置了下來。

這個故事抓住了問題的重點：無窮大的數字的確擁有一些不同于普通數字的古怪特性。

根據康托爾的“無窮數比較法則”，我們現在還能證明分數（例如3/7或者735/8）的數量等于整數的數量。事實上，我們可以根據如下規則將所有分數排成一行：先寫下分子與分母之和等于2的分數，這樣的分數只有一個：1/1；然后寫下分子分母之和等于3的分數：2/1和1/2；接下來是分子分母和為4的：3/1、2/2、1/3。以此類推，最終我們將得到一個包含了所有分數的無限長的數列。現在，我們在這個數列上方寫下整數數列，讓這個數列中的每個項和分數數列一一對應。最后你會發現，分數的數量和整數的數量相等！