- 深圳大學理論經濟學博士后研究報告文集(第一輯)
- 陶一桃主編
- 2479字
- 2022-07-26 18:46:20
6.3 基于博弈模型的數值分析
我們研究納什均衡的存在性和唯一性,原因在于社會網絡博弈模型的結構往往比較復雜,模型的解難以用顯性函數來表示,模型參數變動對解的影響很難通過常規的比較靜態分析來實現。因此,數值分析常常被用來研究這類復雜模型的解的特征。但如果模型存在多個均衡解,搜索納什均衡的計算量可能會非常大,而且很難獲得確定性的結論。因此納什均衡的存在性和唯一性意味著數值方法能夠作為一個合適的工具對解的特征進行分析。這一節的數值分析建立在上文的理論模型基礎之上,主要探討三個問題:①“嫌貧愛富”行為背后的邏輯;②自有資本分布、預算約束與資本實力的關系;③“樂于助人”的社會效益。
6.3.1 數值分析的計算過程
在數值分析的過程中,我們設定對于任意參與者i,自有資本Ai∈(0,1)。預算約束有兩種形式:①預算約束與自有資本正相關,即bi=δAi,?i∈N;②預算約束與自有資本無關,即對所有參與者bi= ,
, 為常數。另外,設f(cij)=
為常數。另外,設f(cij)= 。這個函數滿足連續可微,嚴格遞增的凸函數條件,且f(0)=0,且
。這個函數滿足連續可微,嚴格遞增的凸函數條件,且f(0)=0,且 ′(c)=+∞。為了滿足f(+∞)=1,可以設定γ>1。我們在這一部分的分析中默認設定γ=2。γ的比較靜態分析將專門在第四節進行。數值分析的計算過程可以簡要表述如下:
′(c)=+∞。為了滿足f(+∞)=1,可以設定γ>1。我們在這一部分的分析中默認設定γ=2。γ的比較靜態分析將專門在第四節進行。數值分析的計算過程可以簡要表述如下:
(1)設定參與者人數,即網絡中的節點數。對于任意一個參與者i,隨機生成一個(0,1)區間上的數值,作為Ai。依據Ai生成預算約束bi=δAi或者bi= ,
, 為常數。設定初始策略組合矩陣C為一個零矩陣。
為常數。設定初始策略組合矩陣C為一個零矩陣。
(2)所有參與者依據初始狀態,遵循理性原則,即f′(cij)[uj-f(cji)ui]=f′(cih)[uh-f(chi)ui]和預算約束條件 =bi計算最優策略。所有參與者的新策略構成新的策略矩陣C。
=bi計算最優策略。所有參與者的新策略構成新的策略矩陣C。
(3)新的策略矩陣會導致新的資本實力分布,這個機制由U=[D-f(C)]-1A決定。
(4)重復上述過程,直至前、后兩期U的元素變化率全部小于指定的迭代精度。本文設定的迭代精度為0.1%。
6.3.2 “嫌貧愛富”行為背后的邏輯
模型納什均衡的另外一個特征就是:所有參與者都將較大比例的預算用于維持與富裕參與者的關系,同時給貧窮的參與者送的禮物相對較少。圖6-1展示了一個隨機實驗的例子。在這個例子中,參與者人數為4,f(cij)= ,預算約束設定為bi=0.3Ai,?i,j∈N。每個參與者的特征由兩個變量來描述,即自由資金和均衡狀態下的資本實力。例如,參與者2的自有資金為0.63,均衡狀態下的資本實力為0.95,在圖中描述為(0.63,0.95)。箭頭是指每個參與者為其他參與者付出的成本(時間、禮物等)數量。例如,參與者2給參與者3的數量是0.080,給參與者1的數量是0.023,給參與者4的數量是0.086。參與者2的自有資金數量最多(0.63),也就是說,參與者2是這個簡單網絡中最富有的。而他的資本實力,即可利用資金的最大數量,也是最大的(0.95)。其他參與者送給參與者2的數量最多。任何一個參與者都根據其他參與者的富有程度分配時間和禮物等資源,并且把更多的資源用于維持與相對富有的參與者的關系。
,預算約束設定為bi=0.3Ai,?i,j∈N。每個參與者的特征由兩個變量來描述,即自由資金和均衡狀態下的資本實力。例如,參與者2的自有資金為0.63,均衡狀態下的資本實力為0.95,在圖中描述為(0.63,0.95)。箭頭是指每個參與者為其他參與者付出的成本(時間、禮物等)數量。例如,參與者2給參與者3的數量是0.080,給參與者1的數量是0.023,給參與者4的數量是0.086。參與者2的自有資金數量最多(0.63),也就是說,參與者2是這個簡單網絡中最富有的。而他的資本實力,即可利用資金的最大數量,也是最大的(0.95)。其他參與者送給參與者2的數量最多。任何一個參與者都根據其他參與者的富有程度分配時間和禮物等資源,并且把更多的資源用于維持與相對富有的參與者的關系。
我們可以看到,以最大化資本實力為目的的社交行為(社會網絡博弈)最終會導致一種“嫌貧愛富”的狀態(博弈策略)。這個博弈過程存在唯一的、穩定的納什均衡,說明這種“嫌貧愛富”的狀態很難避免。“最大化資本實力”這一經濟目標客觀上決定了“嫌貧愛富”這一社會狀態。因此,僅僅從主觀上對這一社會狀態進行批判無助于問題的解決。意欲改善社會道德狀況,必須根治導致這一結果的“經濟基礎”。本文的社會網絡博弈模型揭示了一個重要的問題:如果人們只能通過私人關系獲得資金(資本)支持,那么,這必然會導致“嫌貧愛富”的社會狀態。要想從根本上改變人們的行為方式,扭轉“嫌貧愛富”的道德陷阱,就必須從根本上改變人們獲得資金(資本)支持的渠道。
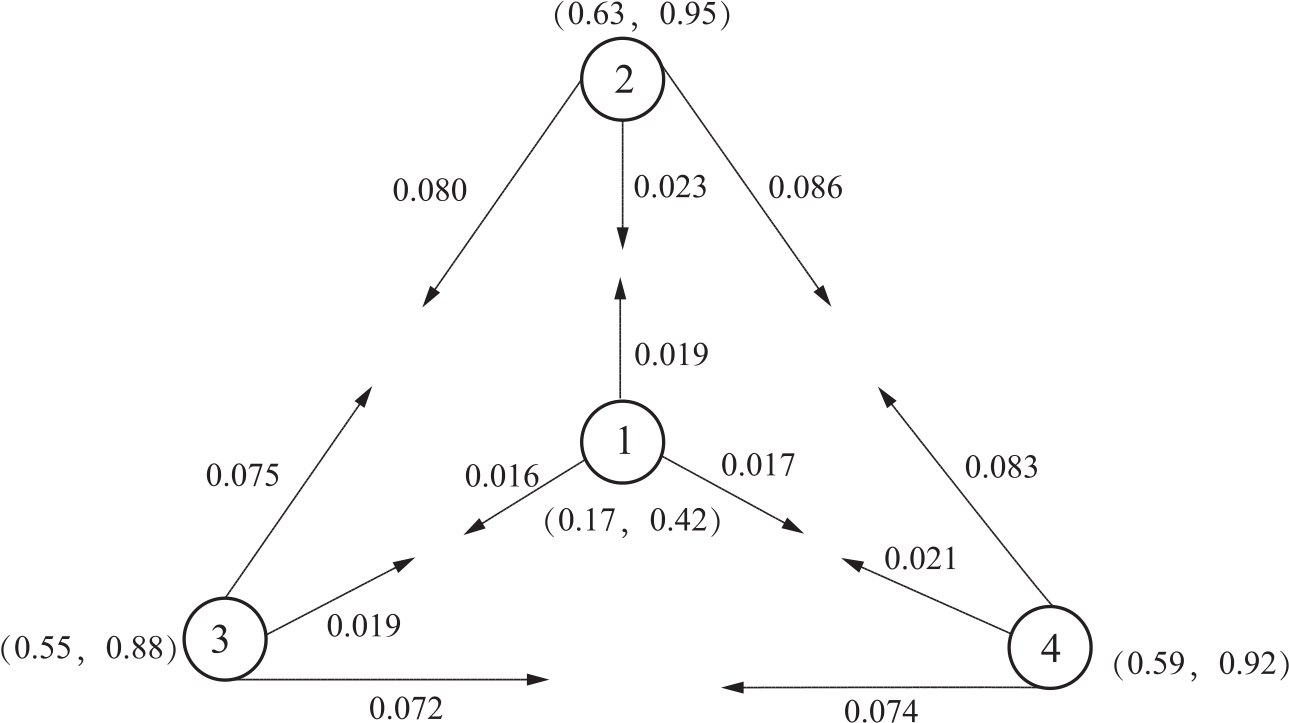
圖6-1 納什均衡時的“嫌貧愛富”
6.3.3 資產分布、預算約束與資本實力
在這一部分中,我們首先設定維持關系的預算占自有資本的比例為30%,即bi=0.3Ai,?i∈N。然后改變關于預算的設定,使所有參與者都面臨相同的預算,即設定bi= =0.3,?i∈N。圖6-2描述了自有資本與資本實力的關系。(62)很顯然,自有資本越多,最終實現博弈均衡時的資本實力就越大。并且隨著參與者人數的增加,每個參與者在自有資本一定的情況下都能夠獲得更大的資本實力。當所有參與者面臨相同的預算約束時,資本實力的分布更加平等。這說明除了自有資本,預算約束同樣也能夠影響均衡狀態下的資本實力分布。
=0.3,?i∈N。圖6-2描述了自有資本與資本實力的關系。(62)很顯然,自有資本越多,最終實現博弈均衡時的資本實力就越大。并且隨著參與者人數的增加,每個參與者在自有資本一定的情況下都能夠獲得更大的資本實力。當所有參與者面臨相同的預算約束時,資本實力的分布更加平等。這說明除了自有資本,預算約束同樣也能夠影響均衡狀態下的資本實力分布。
我們在重復實驗的過程中還計算了每一組實驗的自有資本基尼系數和資本實力基尼系數。兩個基尼系數呈現出明顯的正相關關系。但是相關系數隨著參與者增加、網絡規模變大而不斷減小。參與者人數為5時,資產基尼系數和資本實力基尼系數的相關系數均值為0.7;當參與者變為10時,相關系數均值下降到0.6;參與者為15時,相關系數均值進一步下降到0.5。這說明隨著參與者人數增加、網絡規模的增大,自有資本不平等對資本實力不平等的影響逐漸減弱。
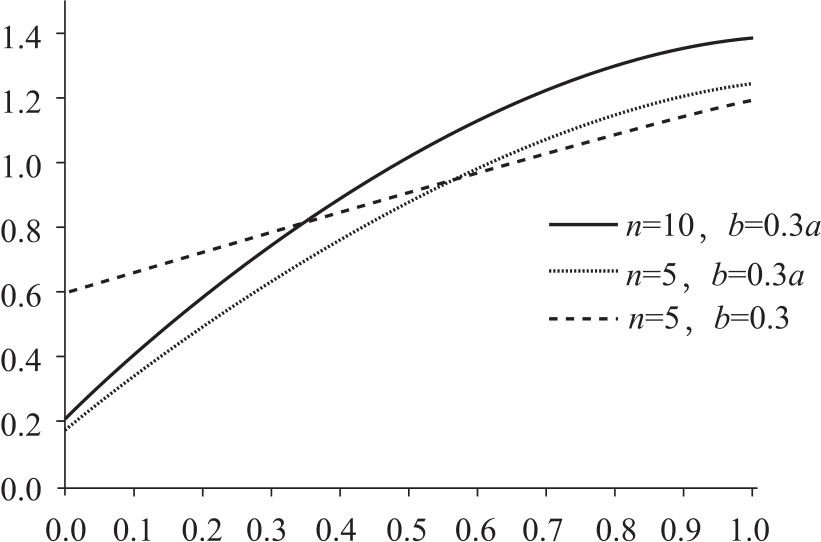
圖6-2 自有資本與資本實力的關系
6.3.4 “樂于助人”的社會效益
在這一部分中,我們改變函數f(cij)= 的參數γ。γ可以反映參與者對其他成員的慷慨程度(熱心程度)。在cij一定的情況下,γ越小,則f(cij)越大,也就是說參與者愿意為朋友提供更多的資金支持。換言之,γ越小,意味著網絡中的參與者越慷慨。反之,則意味著參與者越吝嗇。一個直覺就是,各個成員越慷慨,越愿意為替他人提供幫助,那么,各個參與者能夠運用的資金量就越大。轉換為模型的表述就是,γ越小,博弈均衡實現時各個參與者的u就越大。我們改變γ,重復數值實驗,并且將結果描述在圖6-3中。
的參數γ。γ可以反映參與者對其他成員的慷慨程度(熱心程度)。在cij一定的情況下,γ越小,則f(cij)越大,也就是說參與者愿意為朋友提供更多的資金支持。換言之,γ越小,意味著網絡中的參與者越慷慨。反之,則意味著參與者越吝嗇。一個直覺就是,各個成員越慷慨,越愿意為替他人提供幫助,那么,各個參與者能夠運用的資金量就越大。轉換為模型的表述就是,γ越小,博弈均衡實現時各個參與者的u就越大。我們改變γ,重復數值實驗,并且將結果描述在圖6-3中。
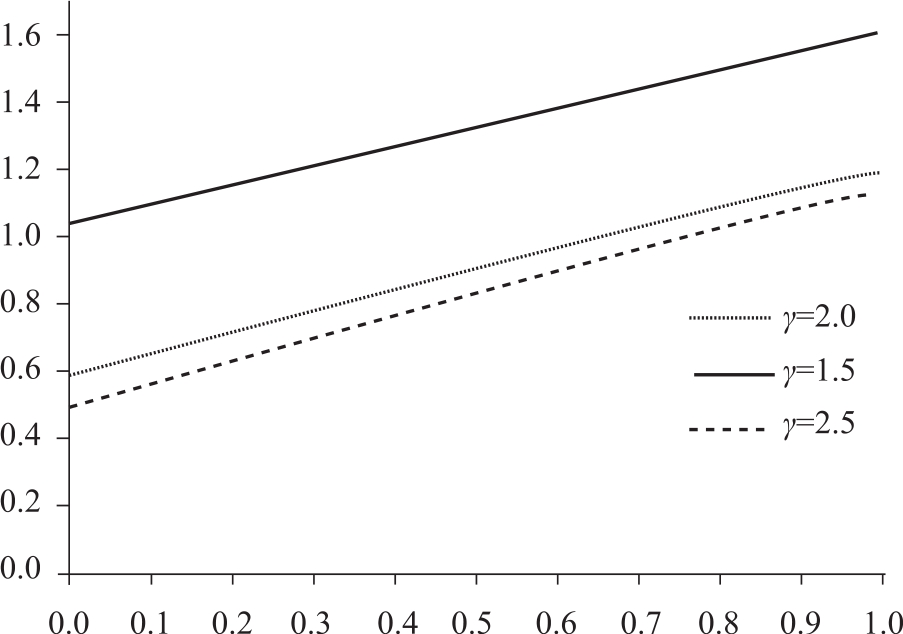
圖6-3 “樂于助人”的社會效應(參數γ的比較靜態分析)
圖6-3所展示的實驗中,參與者人數均為5,預算約束全部與自有資本無關,且bi= =0.3。給定自有資本,當γ=1.5時,均衡狀態下的資本實力最大;而γ=2.5時,均衡的資本實力最小。而且當γ=1.5時,參與者的均衡資本實力明顯大于其他兩種參數狀態下的均衡資本實力。這說明,慷慨地幫助其他成員能夠明顯地提高社會總體資本實力。從這個角度來看,樂于助人的品質可以被理解為一種“社會資本”。這種品質在無形中提高了各個社會成員的資本實力,使他們可以更好地把握住機會。如果每個人都慷慨地幫助其他成員,那么最終每個人的福利都將得到增加,社會總體福利會有顯著的改善。
=0.3。給定自有資本,當γ=1.5時,均衡狀態下的資本實力最大;而γ=2.5時,均衡的資本實力最小。而且當γ=1.5時,參與者的均衡資本實力明顯大于其他兩種參數狀態下的均衡資本實力。這說明,慷慨地幫助其他成員能夠明顯地提高社會總體資本實力。從這個角度來看,樂于助人的品質可以被理解為一種“社會資本”。這種品質在無形中提高了各個社會成員的資本實力,使他們可以更好地把握住機會。如果每個人都慷慨地幫助其他成員,那么最終每個人的福利都將得到增加,社會總體福利會有顯著的改善。