2.4　數(shù)值實(shí)現(xiàn)

2.4.1　人工材料插值模型

在本書(shū)所涉及的研究中，均假設(shè)水平集網(wǎng)格規(guī)模與結(jié)構(gòu)域的有限元網(wǎng)格規(guī)模相當(dāng)。當(dāng)水平集函數(shù)所包含的光滑邊界在規(guī)則Eularian網(wǎng)格上運(yùn)動(dòng)時(shí)，必然會(huì)出現(xiàn)網(wǎng)格被結(jié)構(gòu)邊界切割的情形，從而導(dǎo)致光滑邊界的不連續(xù)問(wèn)題（boundary discontinuity）。通常，需要在迭代過(guò)程中不對(duì)結(jié)構(gòu)域進(jìn)行網(wǎng)格重劃分，以準(zhǔn)確描述水平集的零水平面所形成的邊界[16]。本書(shū)采用人工材料（ersatz material）[20]模型來(lái)解決邊界不連續(xù)問(wèn)題，從而避免耗時(shí)的有限元網(wǎng)格重劃分過(guò)程。在計(jì)算應(yīng)變場(chǎng)時(shí)，人工材料模型假設(shè)被結(jié)構(gòu)邊界切割的單元等效為具有中間密度的單元，初切割單元實(shí)體部分所占的面積代表該單元的人工材料密度值，單元的剛度矩陣則與該人工材料密度值正相關(guān)。

2.4.2　過(guò)濾技術(shù)

在參數(shù)化水平集中，可采用過(guò)濾技術(shù)對(duì)單元偽密度χ_h進(jìn)行過(guò)濾。一方面，無(wú)論是采用光滑的Heaviside函數(shù)[7]還是人工材料模型[8]都無(wú)法完全精準(zhǔn)地表達(dá)結(jié)構(gòu)邊界和設(shè)計(jì)敏度[34]，因此過(guò)濾技術(shù)能夠增加設(shè)計(jì)敏度的光滑性。另一方面，合適的過(guò)濾技術(shù)還能通過(guò)增加偽密度場(chǎng)的連續(xù)性來(lái)緩解拓?fù)鋬?yōu)化設(shè)計(jì)中的網(wǎng)格依賴性問(wèn)題[35]，[36]。

本書(shū)所采用的偽密度過(guò)濾技術(shù)為

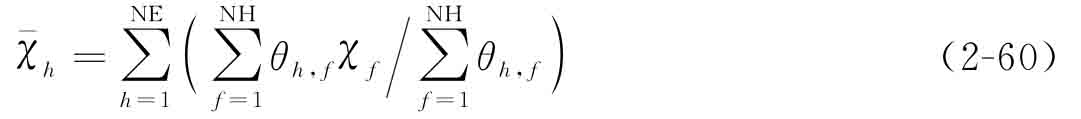
其中，θ_h，_f= 。

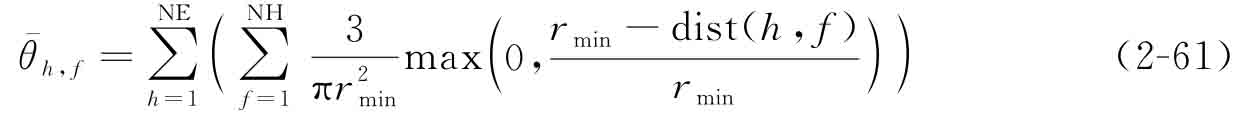
其中， 為過(guò)濾后的單元偽密度；θ_h，_f為hat函數(shù) 所定義的卷積；NH是在單元h附近指定過(guò)濾半徑范圍內(nèi)的單元數(shù)量；r_min為過(guò)濾半徑，通常取值為1.5~2.0倍的網(wǎng)格尺寸；dist(h，f)用于計(jì)算單元h到單元f間的距離。