2.5　優(yōu)化算法

拓?fù)鋬?yōu)化是一類具有大規(guī)模設(shè)計(jì)變量的非線性規(guī)劃問題，優(yōu)化模型的高維度導(dǎo)致其求解困難。根據(jù)拓?fù)鋬?yōu)化模型的不同特點(diǎn)，所采用的優(yōu)化算法也不盡相同。在各類優(yōu)化算法中，基于梯度的優(yōu)化算法具有獨(dú)特的優(yōu)勢[37]。在拓?fù)鋬?yōu)化領(lǐng)域，發(fā)展較為成熟的梯度優(yōu)化算法主要包括優(yōu)化準(zhǔn)則法（optimality criteria，OC）[24]和移動(dòng)漸近線法（method of moving asymptotes，MMA）[25]。MMA是數(shù)學(xué)規(guī)劃法（mathematical programming，MP）中的一種常用方法，具有嚴(yán)謹(jǐn)?shù)睦碚摶A(chǔ)和數(shù)學(xué)推導(dǎo)過程，適用于具有復(fù)雜目標(biāo)函數(shù)和多約束的結(jié)構(gòu)拓?fù)鋬?yōu)化問題。OC法簡單直接、迭代收斂快，對于約束條件較少的大規(guī)模結(jié)構(gòu)優(yōu)化設(shè)計(jì)問題尤為高效。本章將主要采用OC法作為優(yōu)化算法。

在參數(shù)化水平集方法中，設(shè)計(jì)變量α_i是徑向基函數(shù)插值的擴(kuò)展系數(shù)，因此在迭代過程中無法直接指定其固定的上下界限α_max和α_min。然而，在實(shí)際數(shù)值操作中可以給出規(guī)范化設(shè)計(jì)變量 的上下限 ，并以此作為OC法的邊值約束來穩(wěn)定迭代過程。針對所討論的優(yōu)化問題，可構(gòu)建如下OC迭代算法：

步驟1　計(jì)算規(guī)范化的設(shè)計(jì)變量：

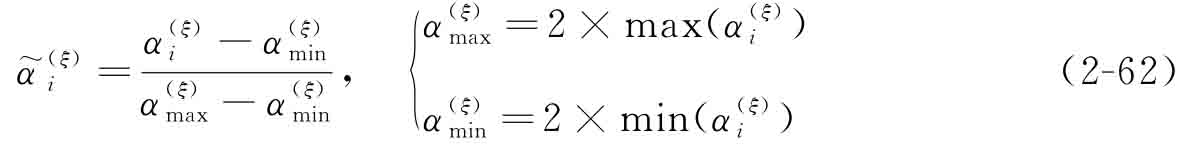
其中，ξ代表當(dāng)前的迭代步。

步驟2　基于Kuhn-Tucker條件[36]，[37]，構(gòu)造如下啟發(fā)式迭代格式更新規(guī)范化設(shè)計(jì)變量

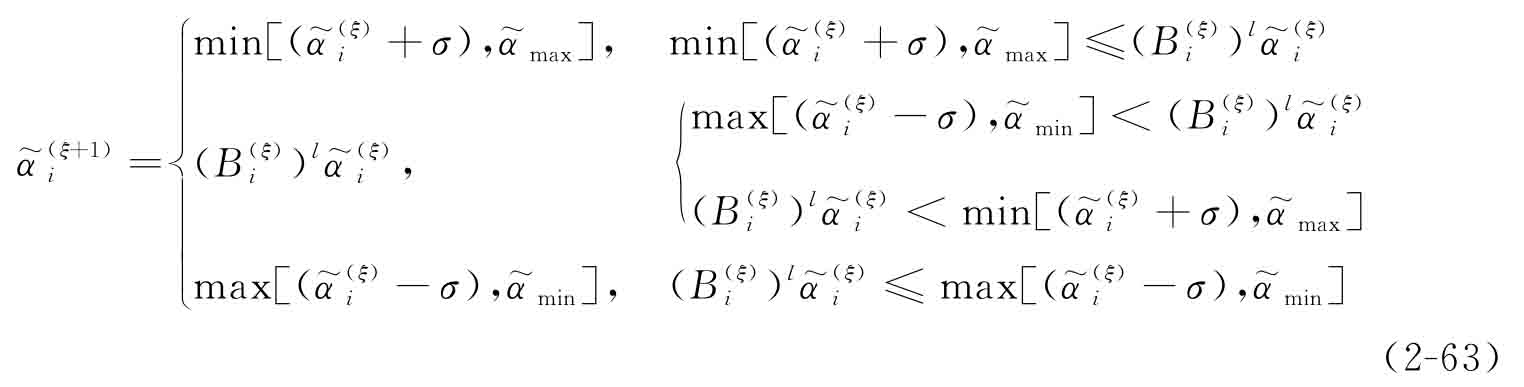
式（2-63）中，引入移動(dòng)極限σ和阻尼算子l以穩(wěn)定優(yōu)化迭代過程，且有0<σ<1和0<l<1。此外，規(guī)范化的設(shè)計(jì)變量上下限分別指定為 =1和 =0.001。 可由下述公式計(jì)算得到：

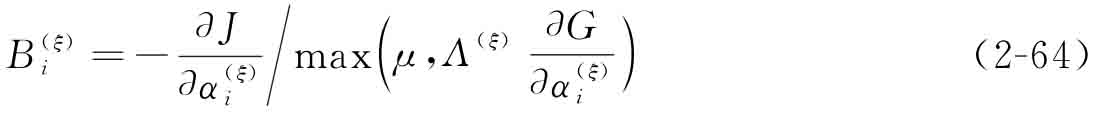
其中，常量μ=1E-10用于避免分母中出現(xiàn)為“0”的項(xiàng)。在每次迭代中，拉格朗日算子由二分法[37]確定。

步驟3　更新設(shè)計(jì)變量：

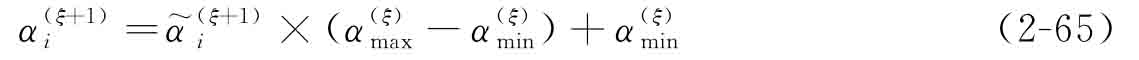
步驟4　重復(fù)步驟1到步驟3直到算法收斂。將第ξ次迭代與第ξ-1次迭代的目標(biāo)函數(shù)之差的絕對值記為γ（ξ），算法的收斂條件為γ（ξ-2）、γ（ξ-1）和γ（ξ）同時(shí)小于0.0001。