書名: Python深度學習:模型、方法與實現作者名: (保加利亞)伊凡·瓦西列夫本章字數: 4815字更新時間: 2021-09-26 16:10:23
1.3 訓練神經網絡
本節把訓練一個神經網絡定義為以最小化代價函數J(θ)的方式調整其參數(權重)的過程。代價函數是對由多個樣本組成的訓練集的性能度量,以向量表示。每個向量都有一個相關的標簽(有監督學習)。最常見的是,代價函數度量網絡輸出和標簽之間的差異。
這一節中,我們將簡要回顧一下梯度下降優化算法。如果你已經熟悉它,可以跳過本節。
1.3.1 梯度下降
本節中,我們使用具有單一回歸輸出和均方誤差(MSE)代價函數的神經網絡,其定義如下:
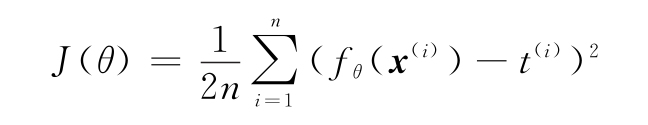
此處,公式解釋如下:
- fθ(x(i))是神經網絡的輸出。
- n是訓練集中的樣本總數。
- x(i)為訓練樣本的向量,上標i表示數據集的第i個樣本。用上標是因為x(i)是一個向量,下標是為每個向量分量保留的。
 例如,是第i個訓練樣本的第j個分量。
例如,是第i個訓練樣本的第j個分量。 - t(i)是與樣本x(i)相關的標簽。
 不應該將第i個訓練樣本的(i)上標指數與代表神經網絡層索引的(l)上標混淆。我們只在梯度下降和代價函數部分使用(i)樣本索引符號,其他部分使用(l)作為層索引符號。
不應該將第i個訓練樣本的(i)上標指數與代表神經網絡層索引的(l)上標混淆。我們只在梯度下降和代價函數部分使用(i)樣本索引符號,其他部分使用(l)作為層索引符號。
首先,梯度下降計算J(θ)分別對所有網絡權重的導數(梯度)。梯度給了我們一個提示,關于J(θ)是如何隨著每一個權重變化的。然后,該算法使用這些信息更新權重,使將來出現相同輸入/目標對時的J(θ)最小化。目標是逐步達到代價函數的全局最小值。下面是MSE和單權重神經網絡的梯度下降可視化表示。
下面逐步執行梯度下降:
1)用隨機值初始化網絡權重。
2)重復操作,直到代價函數低于某個閾值:
(1)前向傳遞:使用前面的公式計算訓練集所有樣本的MSE的J(θ)代價函數。
(2)反向傳遞:用鏈式法則計算J(θ)對所有網絡權重的導數:
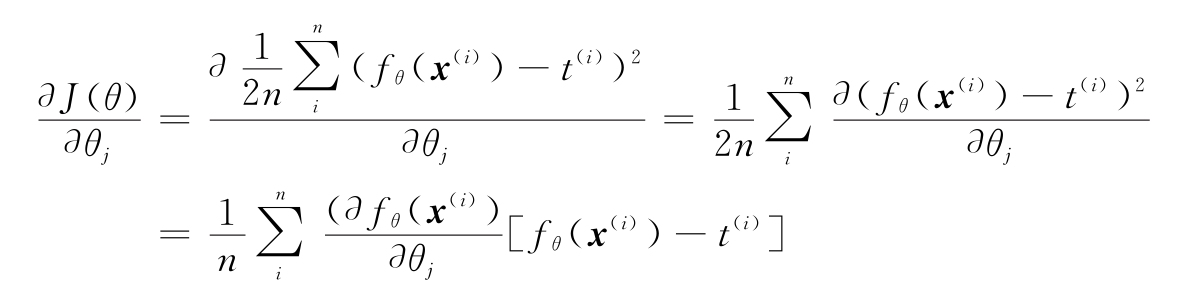
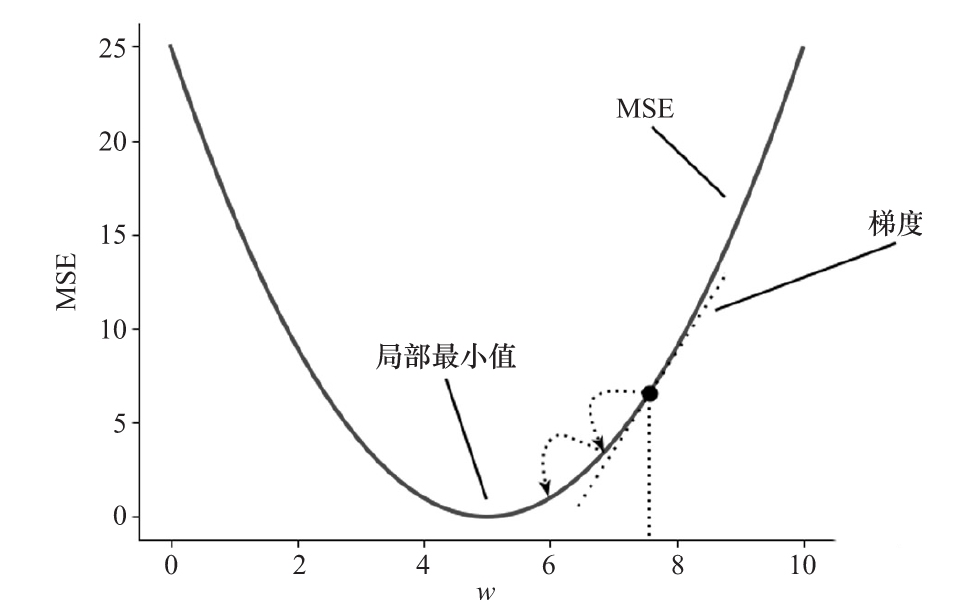
MSE的梯度下降可視化
 分析一下?J(θ)/?θj的導數。J作為網絡輸出的函數,是θj的一個函數。因此,它也是神經網絡函數本身的函數,即J(f(θ))。然后,通過鏈式法則,可以得到
分析一下?J(θ)/?θj的導數。J作為網絡輸出的函數,是θj的一個函數。因此,它也是神經網絡函數本身的函數,即J(f(θ))。然后,通過鏈式法則,可以得到
(3)使用這些導數來更新每個網絡權重:
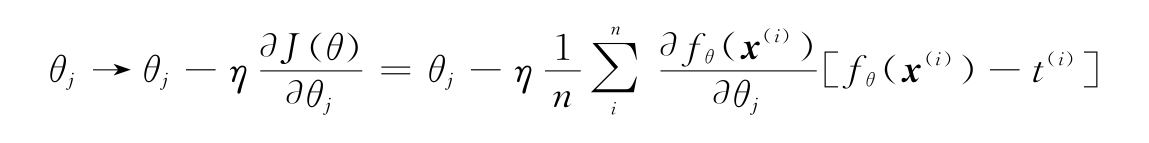
此處,η是學習率。
梯度下降法通過累積所有訓練樣本的誤差來更新權重。實際上,可以使用其中兩項進行修改:
- 隨機(或在線)梯度下降(SGD)在每次訓練樣本后更新權重。
- 小批量梯度下降對每n個樣本(一個小批量)累積誤差,并執行一次權重更新。
接下來,討論一下SGD中可以使用的不同代價函數。
1.3.2 代價函數
除了MSE,還有一些其他的損失函數經常在回歸問題中使用。以下是一份非詳盡的列表:
- 平均絕對誤差(MAE)是網絡輸出和目標之間的絕對誤差(而不是平方)的平均值。MAE的圖和公式見下頁。
-

相對于MSE,MAE的一個優點是它能更好地處理離群樣本。對于MSE,如果樣本的誤差是fθ(x(i))-t(i)>1,它會指數下降(因為平方)。與其他樣本相比,這個樣本的權重過大,這可能會導致結果偏差。在MAE中,差異不是指數級的,這個問題不那么明顯。
另外,MAE梯度會有相同的值,直到達到最小值,它會立即變成0。這使得算法更難預測代價函數的最小值有多接近。與MSE相比,當接近代價最小值時,斜率逐漸減小。這使得MSE更容易優化。綜上所述,除非訓練數據被異常值破壞,否則通常建議在MAE基礎上使用MSE。
- Huber損失試圖通過結合MAE和MSE的屬性來解決兩者的問題。簡而言之,當輸出數據和目標數據之間的絕對差低于一個固定參數的值δ時,Huber損失類似于MSE。相反,當差異大于δ時,它與MAE相似。這樣,它對異常值(差值較大時)的敏感性較低,同時函數的最小值是適當可微的。以下是單一訓練樣本的三種不同的訓練對象的Huber損失圖及其公式,反映了它的二重性。
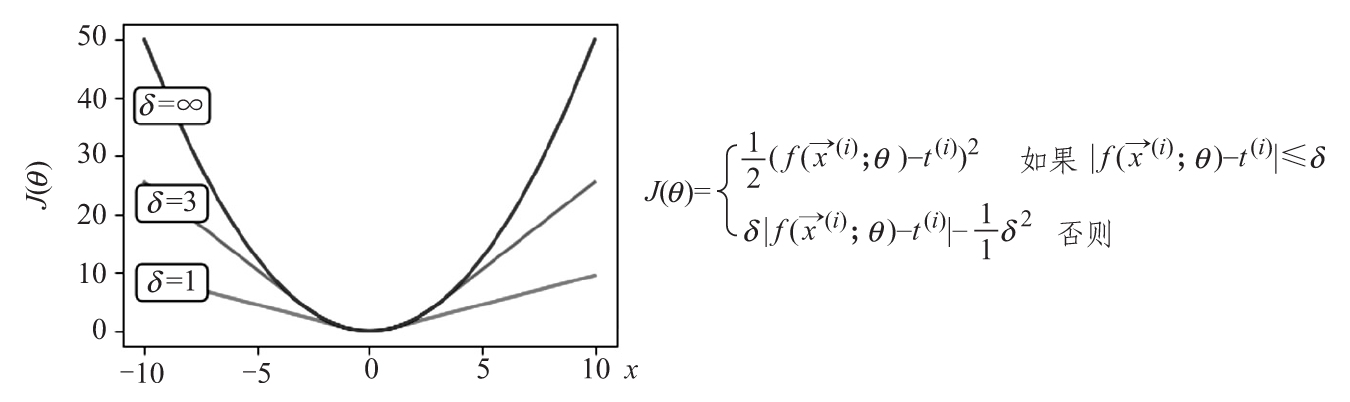
Huber損失
接下來,關注分類問題的代價函數。以下是一份非詳盡的清單:
- 交叉熵損失:這里省略了一些工作,因為1.1.2節已經定義了交叉熵。這種損失通常應用于softmax函數的輸出。這兩者配合得很好。首先,softmax將網絡輸出轉換為概率分布。然后,交叉熵度量網絡輸出(Q)與真實分布(P)的差值,作為訓練標簽提供。它還有另一個好的性質,H(P,Qsoftmax)的導數非常簡單(雖然計算并不簡單):
H′(P,Qsoftmax)=Qsoftmax(x(i))-P(t(i))
此處,x(i)/t(i)是第i個輸入/標簽訓練對。
- KL散度損失:像交叉熵損失一樣,1.1.2節已經對它進行了介紹,并得到KL散度和交叉熵損失之間的關系。其關系可以說明,如果使用兩者中的一個作為損失函數,我們也會隱式地使用另一個。
 有時,會遇到損失函數和代價函數互換使用的情況。人們通常認為它們稍有不同。我們把損失函數稱作訓練集的單個樣本的網絡輸出和目標數據之間的差值。代價函數是相同的,但是對訓練集的多個樣本(批量)進行平均(或求和)。
有時,會遇到損失函數和代價函數互換使用的情況。人們通常認為它們稍有不同。我們把損失函數稱作訓練集的單個樣本的網絡輸出和目標數據之間的差值。代價函數是相同的,但是對訓練集的多個樣本(批量)進行平均(或求和)。
學習不同的代價函數后,把重點放在通過網絡反向傳播的誤差梯度上。
1.3.3 反向傳播
這一節將討論如何更新網絡權重以使代價函數最小化。正如在1.3.1節所論證的,這意味著找到代價函數J(θ)對每個網絡權重的導數。在鏈式法則的幫助下我們已經朝這個方向邁出了一步:
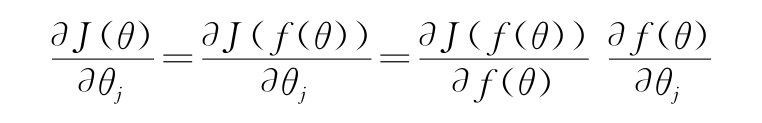
此處,f(θ)是網絡輸出,而θj是第j個網絡權重。在這一節中,我們學習如何推導所有網絡權重的神經網絡函數本身(提示:鏈式法則),通過網絡反向傳播誤差梯度來實現這一點。下面是幾個假設:
- 為了簡單起見,使用順序前饋神經網絡。順序意味著每一層從前一層獲取輸入并將輸出發送到下一層。
- 我們定義wij為第l層的第i個神經元和第l+1層的第j個神經元之間的權重。也就是說,使用下標i和j,其中有下標i的元素屬于包含下標j的元素的層的前面一層。在多層網絡中,l和l+1可以是任意兩個連續的層,包括輸入層、隱藏層和輸出層。
- 用yi(l)表示第l層的第i個單元的輸出,用yj(l+1)表示第l+1層的第j個單元的輸出。
- 用aj(l)表示第l層的第j個單元的激活函數的輸入(即激活前輸入的加權和)。
下面的圖展示了前面介紹的所有符號。
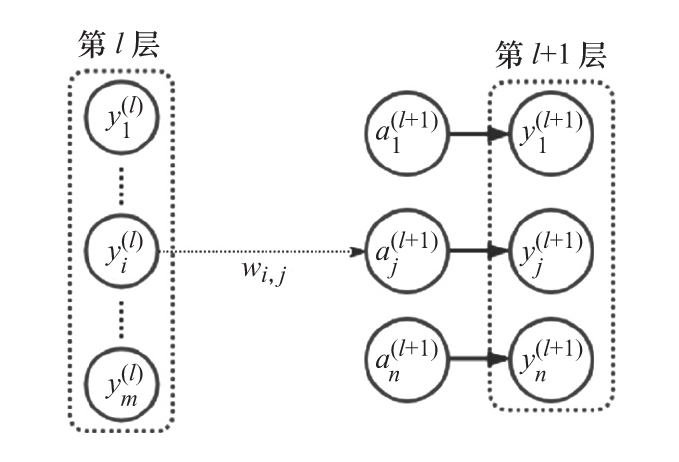
第l層表示輸入,第l+1層表示輸出,wi,j連接第l層中的 對第l+1層中的第j個神經元的激活
對第l+1層中的第j個神經元的激活
有了這些知識鋪墊后,讓我們進入正題:
1)首先,假設l和l+1分別是倒數第二個和最后的(輸出)網絡層。知道了這個,J對wi,j的導數如下:
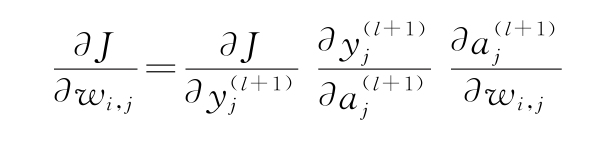
2)讓我們關注?aj(l+1)/?wi,j。此處,計算第l層的輸出對其中一個權重wi,j的加權和的偏導數。正如在1.1.3節中討論的,在偏導數中,將考慮除wi,j常量之外的所有函數參數。當導出aj(l+1)時,它們都變成0,只剩下?(yi(l)wi,j)/?wi,j=yi(l)。因此,可以得到:
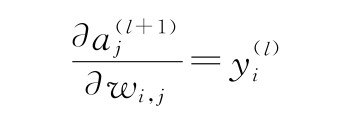
3)對于網絡的任意兩個連續的隱藏層(l和l+1),由第1)步得出的公式都成立。我們了解?(yi(l)wi,j)/?wi,j=yi(l),也知道?yj(l+1)/?aj(l+1)是我們可以計算的激活函數的導數(參見1.2.4節)。需要做的就是計算導數?J/?yj(l+1)(回想一下,此處,第l+1層是某個隱藏層)。我們注意到這是誤差對第l+1層的激活函數的導數。現在可以因為以下應用,從最后一層開始反向移動,計算所有的導數:
- 可以計算最后一層的導數。
- 假設可以計算下一層的導數,有一個公式允許我們計算某一層的導數。
4)記住這些步驟,用鏈式法則得到如下方程:
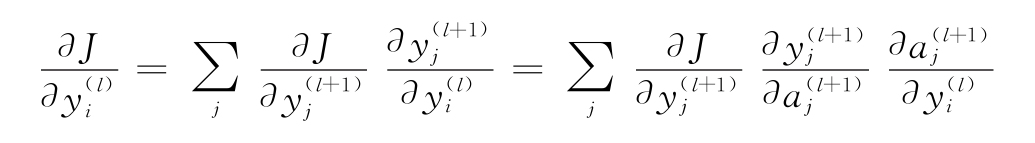
j的和反映了,在網絡的前饋部分,輸出 被反饋給在第l+1層的神經元。因此,當誤差反向傳播的時候它們全都提供給了yi(l)。
被反饋給在第l+1層的神經元。因此,當誤差反向傳播的時候它們全都提供給了yi(l)。
我們可以再一次計算?yj(l+1)/?aj(l+1)。跟著與第3)步相同的邏輯,可以計算?aj(l+1)/?yi(l)=wi,j。因此,一旦知道了?J/?yj(l+1),可以計算?J/?yj(l)。因為可以計算最后一層的?J/?yj(l+1),并且能夠反向計算任意一層的?J/?yj(l),所以我們能計算任意一層的?J/?wi,j。
5)總結一下,假設有一系列層,它適用于以下內容:
yi→yj→yk
此處,有以下基本方程:
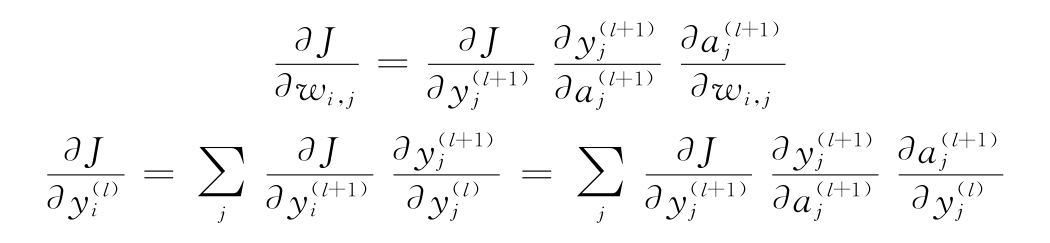
通過使用這兩個方程,可以計算代價對每一層的導數。
6)如果設 ,然后
,然后 表示代價對激活值的變化,可以把
表示代價對激活值的變化,可以把 看作在神經元yj(l+1)處的誤差。可以將這些方程改寫為:
看作在神經元yj(l+1)處的誤差。可以將這些方程改寫為:
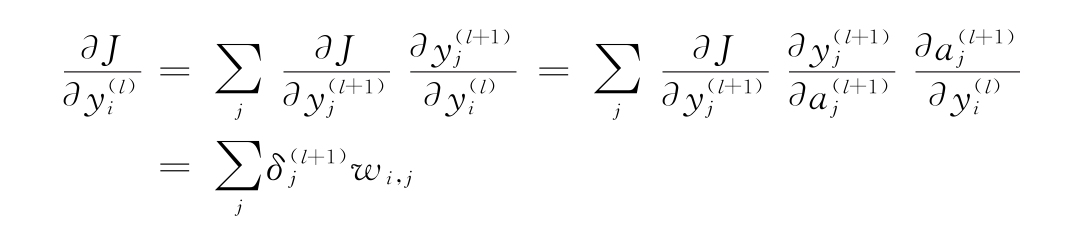
由此,可以得到:
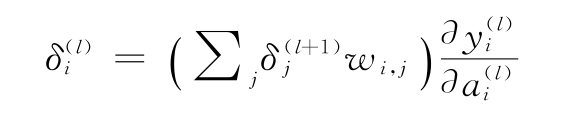
這兩個方程為我們提供了反向傳播的另一種觀點,因為代價隨激活值的變化而變化。一旦知道了下一層(l+1)的變化,它們就為我們提供了計算任意層l的變化的方法。
7)將這些方程組合起來,可以看出:
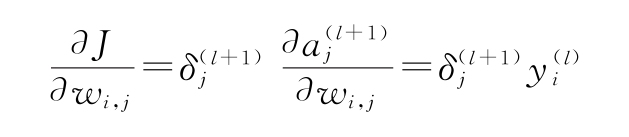
8)各層權重的更新規則如下:
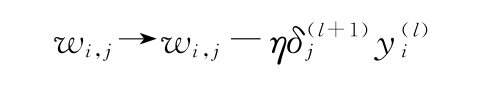
現在熟悉了反向傳播,下面討論訓練過程的另一個組成部分:權重初始化。
1.3.4 權重初始化
深度網絡訓練的一個關鍵組成部分是隨機權重初始化。這很重要,因為有些激活函數,如sigmoid和ReLU,只有它們的輸入在一定范圍內,才會產生有意義的輸出和梯度。
一個著名的例子就是梯度消失問題。為了理解它,考慮一個具有sigmoid激活的FC層(這個示例對tanh也有效)。1.2.4節展示了sigmoid函數及其導數。如果輸入的加權和落在(-5,5)范圍之外,sigmoid激活實際上變為0或1。本質上,它是飽和的。這在推導sigmoid的反向傳遞過程中是可見的(公式是σ′=σ(1-σ))。可以看到,在相同的(-5,5)輸入范圍內,導數大于0。因此,無論試圖傳播回之前的層的誤差是什么,如果激活不在這個范圍內,它就會消失(這就是該名稱的來源)。
 除了sigmoid導數的嚴格意義范圍外,我們注意到,即使在最佳條件下,其最大值也只有0.25。當把梯度傳播到sigmoid導數,一旦通過,最小會變為其1/4。因此,即使沒有落在期望的范圍之外,梯度也可能會在幾個層中消失。這是sigmoid相對于*LU函數族的主要缺點之一,在大多數情況下,梯度為1。
除了sigmoid導數的嚴格意義范圍外,我們注意到,即使在最佳條件下,其最大值也只有0.25。當把梯度傳播到sigmoid導數,一旦通過,最小會變為其1/4。因此,即使沒有落在期望的范圍之外,梯度也可能會在幾個層中消失。這是sigmoid相對于*LU函數族的主要缺點之一,在大多數情況下,梯度為1。
解決這個問題的一種方法是使用*LU激活。但即便如此,使用更好的權重初始化還是有意義的,因為它可以加速訓練過程。一種流行的技術是使用Xavier/Glorot初始化器(http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf)。簡而言之,這種技術考慮了單元的輸入和輸出連接的數量。它有兩種變體:
- Xavier均勻初始化,它從范圍[-a,a]的均勻分布中抽取樣本。參數a的定義如下:
-

此處nin和nout分別表示輸入和輸出的數量(即輸出到當前單元的單元數和當前單元輸出的單元數)。
- Xavier正態初始化,從均值為0、方差為0的正態分布(見1.1.2節)中抽取樣本如下:
-

建議對sigmoid或tanh激活函數進行Xavier/Glorot初始化。論文“Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”(https://arxiv.org/abs/1502.01852)中,提出了一種類似的更適合ReLU激活的技術。同樣,它有兩種變體:
- He均勻初始化,它從范圍[-a,a]的均勻分布中抽取樣本。參數a的定義如下:
-

- He正態初始化,從均值為0、方差為0的正態分布中抽取樣本如下:
-

當輸入為負時,ReLU輸出總是0。如果假設ReLU的初始輸入集中在0附近,那么半數的ReLU輸出為0。與Xavier初始化相比,He初始化通過增加兩次方差來彌補這一點。
下一節將討論對標準SGD的權重更新規則的一些改進。
1.3.5 SGD改進
我們將從動量開始,它通過使用先前權重更新的值來調整當前權重更新,并擴展SGD。也就是說,如果第t-1步的權重更新較大,會增加第t步的權重更新。可以用類比來解釋動量。把損失函數的表面想象成小山的表面。現在,假設拿著一個球在山頂(最大值)。如果把球扔下去,由于地球的重力,它會開始滾向山底(最小值)。它滾動的距離越遠,速度就越快。換句話說,它將獲得動量。
現在,討論如何在權重更新規則中實現動量。回顧我們在1.3.1節中介紹的更新規則,θj→θj-η?J(θ)/?θj。假設在訓練過程的第t步:
1)首先,通過包含之前更新的速度vt-1,計算當前權重更新值vt:
vt→μvt-1-η?J(θ)/?θj
此處,μ是一個在[0:1]范圍內的超參數,稱為動量率。在第一次迭代中,vt被初始化為0。
2)然后,執行實際的權重更新:
θj→θj+vt
對基本動量的改進是Nesterov動量。它依賴于觀察到第t-1步的動量可能不能反映第t步的條件。例如,在第t-1步的梯度很陡,因此動量很高。然而,在第t-1步的權重更新后,實際上達到了代價函數的最小值,只需要在t時刻進行較小的權重更新。盡管如此,仍然會從t-1得到較大的動量,這可能會導致調整后的權重跳過最小值。Nesterov動量提出了改變計算權重更新速度的方式——根據代價函數的梯度來計算vt,它是由權重θj的潛在未來值來計算的。更新后的速度公式如下:
vt→μvt-1-η?J(θ;θj+μvt-1)/?θj
如果t-1處的動量相對于t處的不正確,則改進的梯度會在相同的更新步驟中補償該誤差。
接下來,討論一下Adam自適應學習率算法(“Adam: A Method for Stochastic Optimization”,https://arxiv.org/abs/1412.6980)。它根據以前的權重更新(動量)計算每個權重的個體和自適應學習率。讓我們討論它是如何工作的:
1)首先,需要計算梯度的一階矩(或均值)和二階矩(或方差):
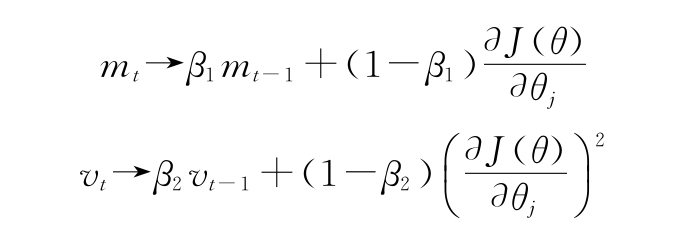
此處,β1和β2是超參數,默認值分別為0.9和0.999。mt和vt作為梯度的移動平均值,類似于動量。它們在第一次迭代中被初始化為0。
2)因為m和v從0開始,所以在訓練的初始階段,它們會偏向于0。例如,在t-1處,β1=0.9并且?J(θ)/?θj=10。此處,m1=0.9*0+(1-0.9)*10=1,這比實際為10的梯度小了很多。為了補償這個偏差,計算mt和vt的偏差修正版本:
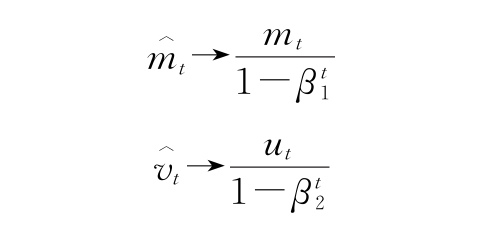
3)最后,需要使用以下公式進行權重更新:
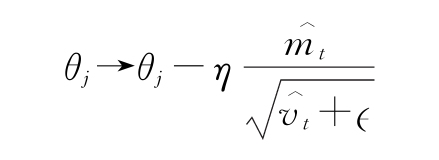
此處,η是學習率, 是防止被0整除的一些小值。
是防止被0整除的一些小值。
- 數字媒體應用教程
- LabVIEW程序設計基礎與應用
- C語言程序設計(第3版)
- Azure IoT Development Cookbook
- Android NDK Beginner’s Guide
- Apex Design Patterns
- jQuery開發基礎教程
- Getting Started with NativeScript
- Apache Kafka Quick Start Guide
- Lighttpd源碼分析
- INSTANT Adobe Edge Inspect Starter
- Mastering Docker
- C指針原理揭秘:基于底層實現機制
- Hands-On Data Visualization with Bokeh
- PHP面試一戰到底