- Python深度學習:模型、方法與實現
- (保加利亞)伊凡·瓦西列夫
- 5016字
- 2021-09-26 16:10:23
1.2 神經網絡的簡單介紹
神經網絡是一個函數(用f表示),它試圖近似另一個目標函數g,可以用以下公式來描述這種關系:
g(x)≈fθ(x)
在此處,x為輸入數據,而θ是神經網絡的參數(權值)。目標是找到這樣的最佳近似函數g的超完備參數θ。這個通用的定義適用于兩者:回歸(近似g的精確值)和分類(將輸入分配到多個可能的類中的一個類)任務。神經網絡函數也可以表示為f(x;θ)。
我們將從神經網絡的最小組成部分——神經元開始討論。
1.2.1 神經元
前面的定義是神經網絡的鳥瞰圖。現在討論神經網絡的基本構件,即神經元(或單元)。單元是數學函數,其定義如下:
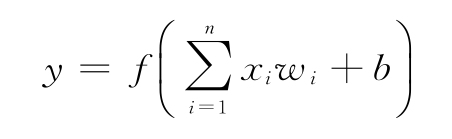
公式解釋如下:
- y是輸出單元(單值)。
- f是非線性可微激活函數。在神經網絡中,激活函數是神經網絡中非線性的來源——如果神經網絡是完全線性的,它只能近似其他線性函數。
- 激活函數的參數是所有輸入單元xi(n為總輸入)和偏置權重b的加權和(權重wi)。輸入xi可以是數據輸入值,也可以是其他單元的輸出。
另外,可以用其向量表示替換xi和wi,其中x=(x1,x2,…,xn),w=(w1,w2,…,wn)。此處,公式將使用兩個向量的點積:
y=f(x·w+b)
下圖(左)顯示了一個神經元。
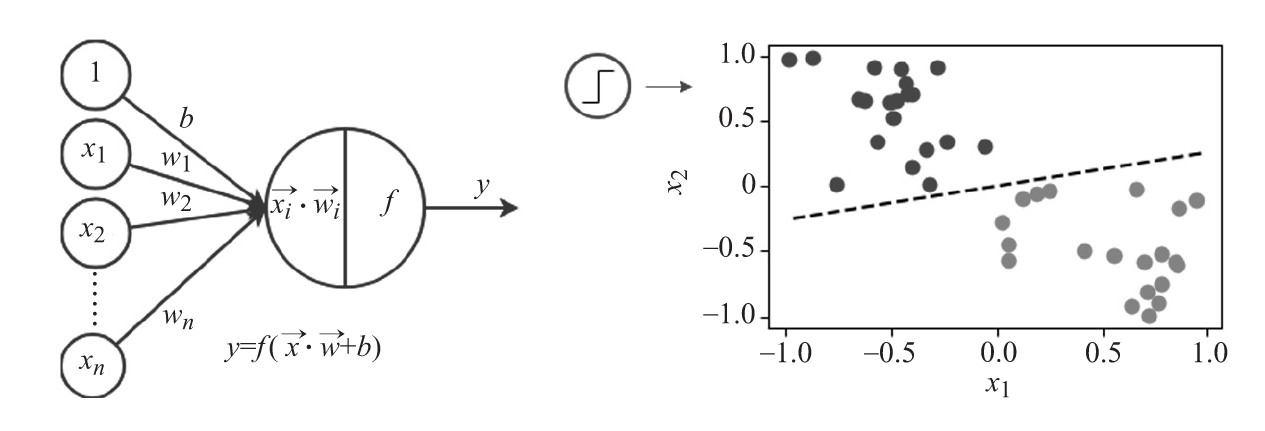
左:一個單元及其等價公式;右:感知器的幾何表示
如果x·w=0,輸入向量x將垂直于權重向量w。因此,所有在x·w=0處的x定義了一個向量空間?n中的超平面,其中n是x的維數。在二維輸入(x1,x2)的情況下,可以將超平面表示為一條直線。這可以用感知器(或二元分類器)來說明,感知器是一個有閾值激活函數 的神經元,可以將輸入分為兩類中的一個。有兩個輸入(x1,x2)的感知器的幾何表示是分隔這兩個類的一條線(或判定邊界)(上述圖的右圖)。這給神經元帶來了嚴重的限制,因為它不能對線性不可分問題進行分類,即使是像XOR這樣簡單的問題。
的神經元,可以將輸入分為兩類中的一個。有兩個輸入(x1,x2)的感知器的幾何表示是分隔這兩個類的一條線(或判定邊界)(上述圖的右圖)。這給神經元帶來了嚴重的限制,因為它不能對線性不可分問題進行分類,即使是像XOR這樣簡單的問題。
具有恒等激活函數(f(x)=x)的單元等價于多元線性回歸,具有sigmoid激活函數的單元等價于邏輯回歸。
接下來,學習如何分層組織神經元。
1.2.2 層的運算
神經網絡組織結構的下一層是單元層,其中將多個單元的標量輸出組合在一個輸出向量中。層中的單元沒有互相連接。這種組織結構有其合理性,原因如下:
- 可以將多元回歸推廣到一個層,而不是單一單元的線性回歸或邏輯回歸。換句話說,可以用一個層來近似多個值,而不是用一個單元來近似單個值。這種情況發生在分類輸出的情況下,其中每個輸出單元表示輸入屬于某個類的概率。
- 一個單元可以傳遞有限的信息,因為它的輸出是標量。通過組合單元輸出,而不是單個激活,可以考慮整個向量。這樣,就可以傳遞更多的信息,不僅因為向量有多個值,而且因為它們之間的相對比率具有額外的含義。
- 因為層中的單元彼此之間沒有連接,所以可以將它們的輸出計算并行化(從而提高計算速度)。這種能力是近年來DL成功的主要原因之一。
在經典的神經網絡(即DL之前的神經網絡,當時它們只是許多ML算法中的一種)中,層的主要類型是全連接(FC)層。在這一層中,每個單元從輸入向量x的所有分量接收加權輸入。假設輸入向量的大小為m,FC層有n個單元和一個激活函數f,這對于所有的單元都是一樣的。n個單元中的每一個都有m個權重,一個權重對應m個輸入中的一個。下面是FC層單個單元j的輸出公式。其與1.2.1節中定義的公式相同,但此處將包含單元索引:
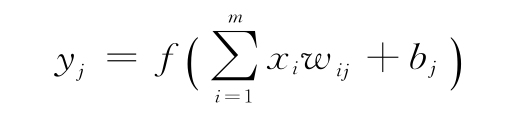
此處,wij為第j層單元與第i個輸入分量之間的權重。可以將連接輸入向量和單元的權重表示為一個m×n的矩陣W。每個矩陣列表示一個層單元的所有輸入的權重向量。在本例中,該層的輸出向量是矩陣-向量乘法的結果。但是,也可以將多個輸入樣本xi組合成一個輸入矩陣(或批量)X,它將同時通過該層。這種情況下,使用矩陣-矩陣乘法,其層輸出是一個矩陣。下圖是一個FC層的示例,以及批量和單例場景中的等效公式:
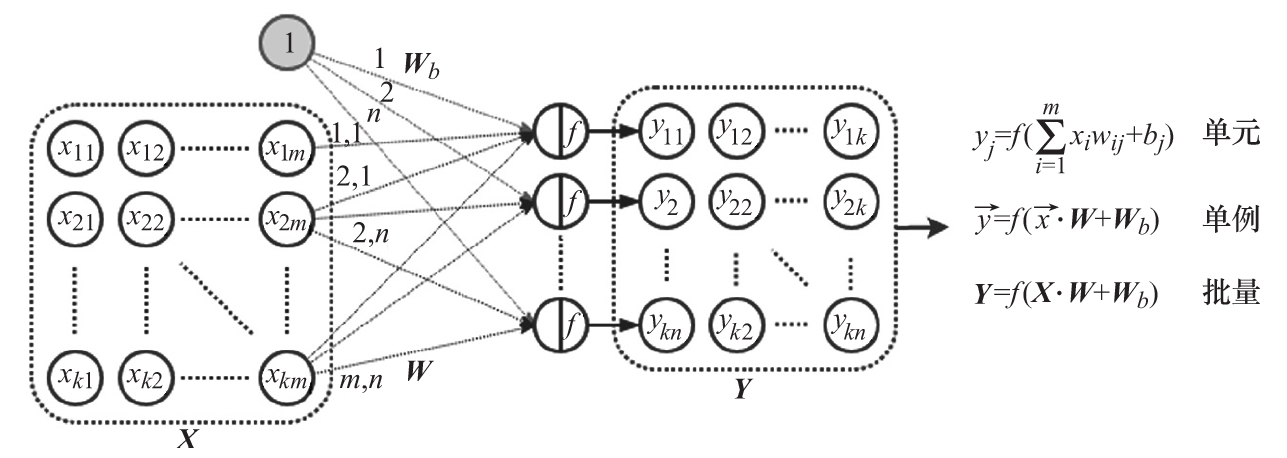
具有向量/矩陣輸入和輸出及其等價公式的FC層
我們明確地分離了偏差矩陣和輸入權重矩陣,但在實踐中,底層實現可能使用共享的權重矩陣,并在輸入數據中附加一行1。
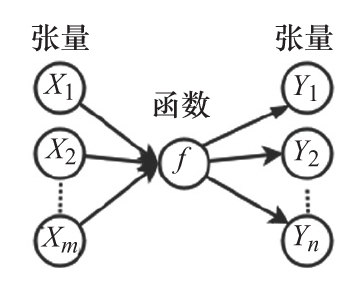
一個具有輸入張量和輸出張量的函數
DL不限于FC層,還有許多其他類型,比如卷積層、池化層等。有些層具有可訓練的權重(FC層、卷積層),而其他層沒有(池化層)。還可以將術語函數或運算與層互換使用。例如,在TensorFlow和PyTorch中,剛才描述的FC層是兩個順序運算的組合。首先,執行權重和輸入的加權和,然后將結果作為輸入提供給激活函數運算。實踐中(使用DL庫的時候),神經網絡的基本構造塊不是單元,而是以一個或多個張量為輸入并輸出一個或多個張量的運算。
接下來,討論如何在一個神經網絡中組合層運算。
1.2.3 神經網絡
在1.2.1節,我們證明了一個神經元(對層也有效)只能分類線性可分的類。為了克服這一限制,必須在一個神經網絡中組合多個層。把神經網絡定義為運算的有向圖(或層)。圖節點是運算,它們之間的邊決定了數據流。如果兩個運算是相連的,那么第一個運算的輸出張量將作為第二個運算的輸入,這個輸入由邊的方向決定。一個神經網絡可以有多個輸入和輸出——輸入節點只有傳出邊,而輸出節點只有傳入邊。
根據這一定義,可以確定兩種主要類型的神經網絡:
- 前饋神經網絡,用無環圖表示。
- 循環神經網絡(RNN),用循環圖表示。循環是暫時性的;圖中的回路連接傳播t-1時刻某個運算的輸出,并將其反饋給下一個時刻t的網絡。RNN保持一種內部狀態,它代表了之前所有網絡輸入的一種總結。這個總結以及最新的輸入被提供給RNN。網絡產生一些輸出,但也更新它的內部狀態,并等待下一個輸入值。這樣,RNN就可以接受長度可變的輸入,比如文本序列或時間序列。
下圖是這兩種網絡的一個例子。
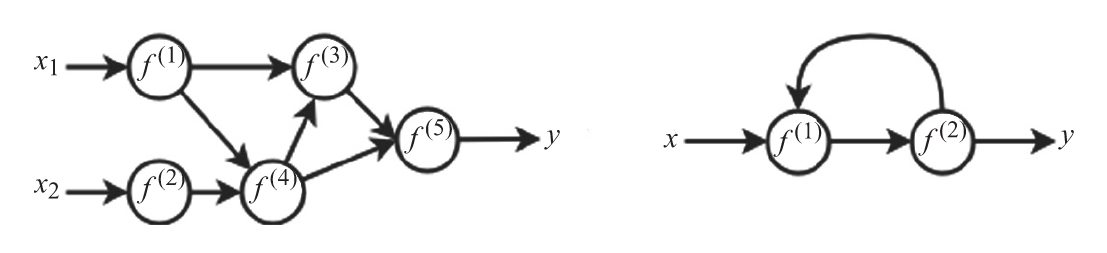
左:前饋網絡;右:循環網絡
假設,當一個運算接收到來自多個運算的輸入時,使用元素依次求和來組合多個輸入張量。然后,可以把神經網絡表示為一系列嵌套的函數或運算。用f(i)(x)表示神經網絡,其中i是幫助我們區分多種運算的一些索引值。例如,上圖中左邊的前饋網絡的等效公式如下:
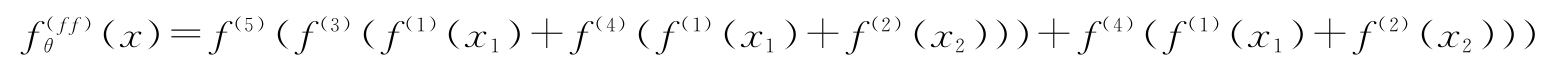
在圖右側的RNN公式為:
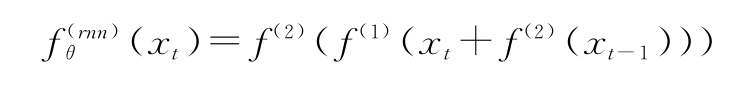
用與運算本身相同的索引表示運算的參數(權重)。取一個索引為l的FC網絡層,它從索引為l-1的前一層獲取輸入。以下是帶有層索引的單個單元和向量/矩陣層表示的層公式:
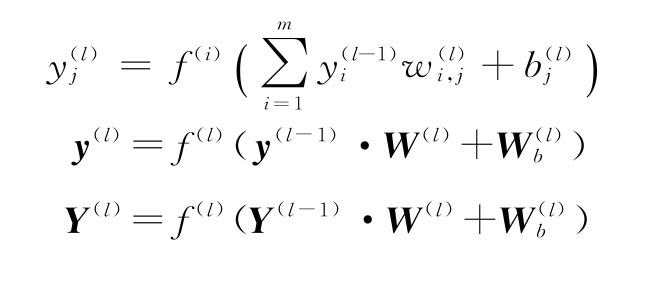
我們已經熟悉了完整的神經網絡架構,現在討論不同類型的激活函數。
1.2.4 激活函數
讓我們討論不同類型的激活函數,從經典的開始:
- sigmoid:它的輸出邊界在0和1之間,可以解釋為神經元激活的概率。由于這些性質,長期以來,sigmoid是最常用的激活函數。然而,它也有一些不太受歡迎的特性(稍后會詳細介紹),這導致了它的受歡迎程度下降。下圖展示了sigmoid公式、它的導數以及其圖像(在我們討論反向傳播時導數很有用)。
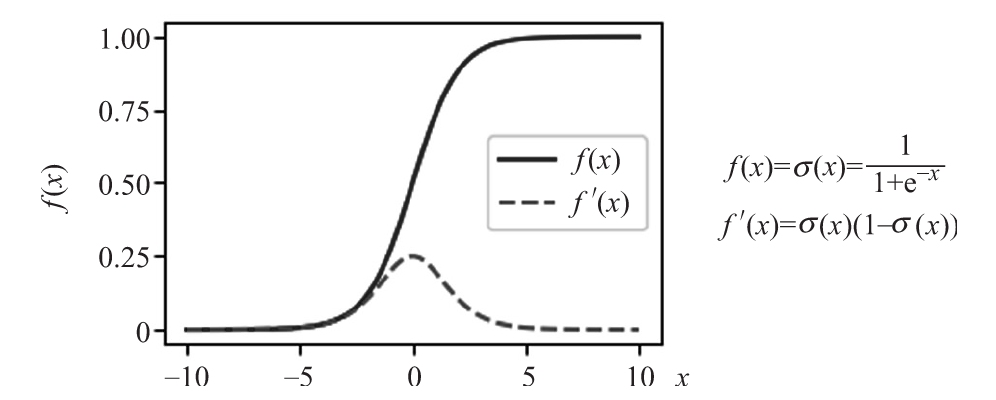
sigmoid激活函數
- 雙曲正切(tanh):這個名字說明了一切。與sigmoid的原則性區別是tanh在(-1,1)內。下圖展示了tanh公式及其導數。
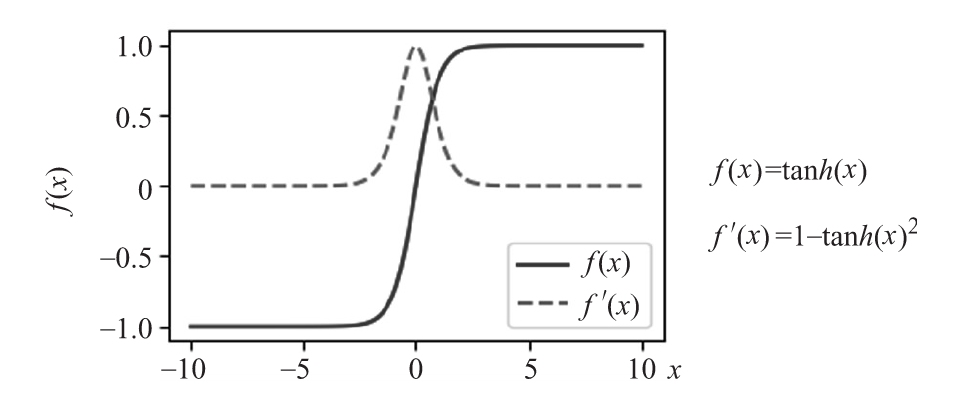
雙曲正切激活函數
接下來,關注這個模塊的“新人”——函數家族的*LU(LU代表線性單元)。從線性整流函數(ReLU)開始,它在2011年首次成功使用(“Deep Sparse Rectifier Neural Networks”,http://proceedings.mlr.press/v15/glorot11a/glorot11a.pdf)。下頁圖給出ReLU公式及其導數。
正如我們所看到的,當x>0時,ReLU重復它的輸入,反之則保持為0。與sigmoid和tanh相比,這種激活函數有幾個重要的優勢:
- 它的導數有助于防止梯度消失(在1.3.4節有更多介紹)。嚴格地說,ReLU在值為0處的導數是未定義的,這使得ReLU只能是半可微的(更多信息可以在https://en.wikipedia.org/wiki/Semidifferentiability上找到)。但在實踐中,它運行得很好。
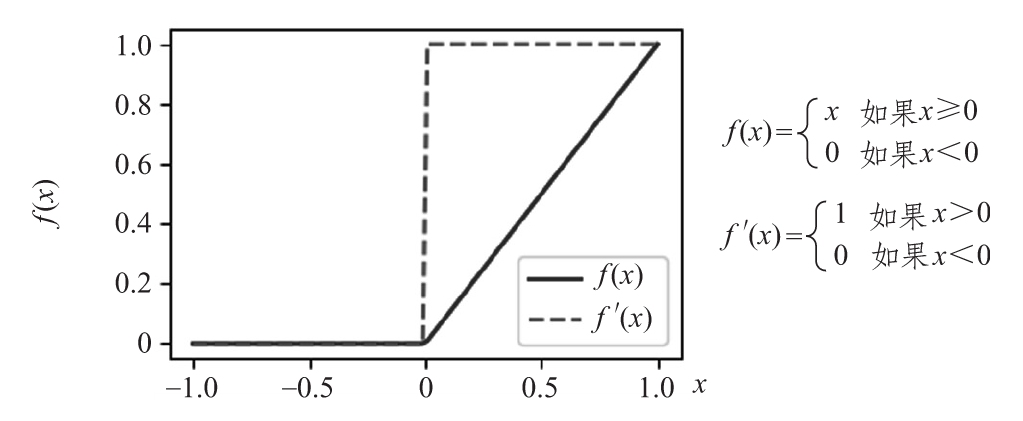
ReLU激活函數
- 它是冪等的——如果傳遞一個值給任意數量的激活函數,它不會改變。例如ReLU(2)=2,ReLU(ReLU(2))=2,依此類推。對于sigmoid,情況不是這樣的,它的值在每次傳遞時都被壓縮:σ(σ(2))=0.707。下圖是一個sigmoid激活函數連續三次激活的例子。
-

連續激活sigmoid函數“壓縮”數據
ReLU的冪等性使其在理論上可以創建比sigmoid層更多的網絡。
- 它創建了稀疏激活——讓我們假設網絡的權值是通過正態分布隨機初始化的。此處,每個ReLU單元的輸入都有0.5的概率小于0。因此,大約一半的激活函數的輸出也是0。稀疏激活有許多優點,可以將其粗略地概括為在神經網絡環境中的奧卡姆剃刀——使用更簡單的數據表示比使用復雜的數據表示能更好地得到相同的結果。
- 前向和反向傳遞的計算速度都比sigmoid的計算速度更快。
然而,在訓練時,網絡權值可以更新為這樣一種方式,即某一層中的ReLU單元總是接收到小于0的輸入,從而使它們也永久地輸出為0。這種現象被稱為“dying ReLU”。為了解決這個問題,對ReLU進行一些修改。以下是一份不太詳盡的列表:
- Leaky(泄漏)ReLU:當輸入大于0時,Leaky ReLU會像常規ReLU一樣重復輸入。但是,當x<0時,Leaky ReLU輸出的是x乘以某個常數α(0<α<1),而不是0。下面的圖給出了Leaky ReLU公式、它的導數,以及其對應的圖。
-

Leaky ReLU激活函數
- 參數化ReLU(PReLU,“Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification”,https://arxiv.org/abs/1502.01852):該激活與Leaky ReLU相同,但參數α是可調的,并在訓練期間進行調整。
- 指數線性單元(ELU,“Fast and Accurate Deep Network Learning by Exponential Linear Units(ELU)”,https://arxiv.org/abs/1511.07289):當輸入大于0時,ELU和ReLU一樣重復輸入。但是,當x<0時,ELU輸出變為f(x)=α(ex-1),其中α是可調參數。下圖為α=0.2時的ELU公式、它的導數及其對應的圖。
-

ELU激活函數
- 縮放指數線性單元(SELU,“Self-Normalizing Neural Networks”,https://arxiv.org/abs/1706.02515):這個激活類似于ELU,區別為輸出(都小于或大于0)是根據額外的訓練參數λ來縮放。SELU是一個更大的概念——自歸一化神經網絡(SNN)的一部分,它在上述論文中有描述。SELU公式如下:
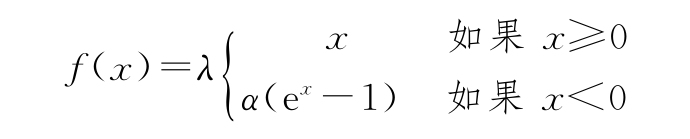
最后,我們將提到softmax,它是分類問題中輸出層的激活函數。假設最終網絡層的輸出是一個向量z=(z1,z2,…,zn),其中n個分量代表輸入數據屬于n個可能的類中的一個的概率。此處,每個向量分量的softmax輸出如下:
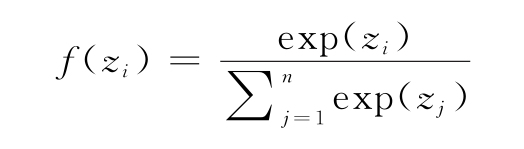
這個公式中的分母可以作為一個歸一化器。softmax輸出有一些重要的屬性:
- 每個f(z)的值都在[0,1]范圍內。
- z的值的總和等于1:∑jf(zj)=1。
- 一個額外的好處(實際上是必需的)是這個函數是可微的。
換句話說,可以將softmax輸出解釋為一個離散隨機變量的概率分布。然而,它還有一個特性。在歸一化數據之前,用指數ezi變換每個向量分量。假設兩個向量分量是z1=1和z2=2。此處exp(1)=2.7,exp(2)=7.39。正如所看到的,變換前后各分量的比率差別很大——0.5和0.36。實際上,與較低的分數相比,softmax提高了獲得較高分數的可能性。
下一節將把注意力從神經網絡的構建模塊轉移到它的整體上。更具體地說,我們將演示神經網絡如何近似任意函數。
1.2.5 通用逼近定理
通用逼近定理在1989年被首次證明,通過具有sigmoid激活函數的神經網絡,然后在1991年,通過具有任意非線性激活函數的神經網絡被再次證明。它指出,在?n的緊致子集上的任意連續函數可以由具有至少一個隱藏層、有限單元數和非線性激活的前饋神經網絡逼近到任意準確率。雖然具有單一隱藏層的神經網絡在很多任務中表現不佳,但該定理仍然告訴我們,在神經網絡中沒有理論上不可逾越的限制。這個定理的正式證明太復雜了,此處無法解釋,但我們將嘗試用一些基礎數學來提供一個直觀的解釋。
 下面這個例子的靈感來自Michael A.Nielsen的書Neural Networks and Deep Learning(http://neuralnetworksanddeeplearning.com/)。
下面這個例子的靈感來自Michael A.Nielsen的書Neural Networks and Deep Learning(http://neuralnetworksanddeeplearning.com/)。
實現一個近似方脈沖函數的神經網絡(如下圖所示),這是一個簡單類型的階梯函數。由于一系列階梯函數可以逼近?n的一個緊子集上的任何連續函數,這將使我們了解為什么通用逼近定理成立。
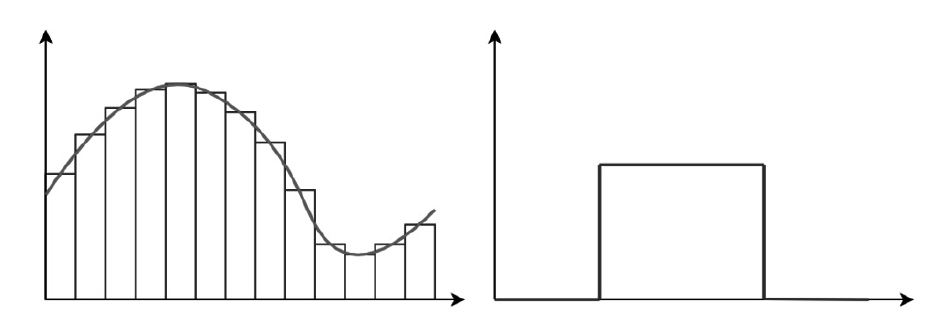
左邊的圖表描述了一系列階梯函數的連續函數近似;
右邊的圖表說明了一個單一的方脈沖階梯函數
為了理解這個近似是如何工作的,從具有單標量輸入x和sigmoid激活的單個單元開始。以下是該單元的可視化表示及其等效公式:
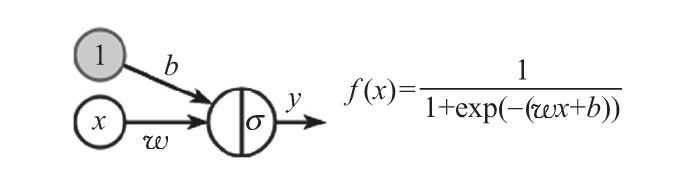
在下面的圖中,可以看到在[-10,10]范圍內輸入不同的b和w值的公式曲線圖。
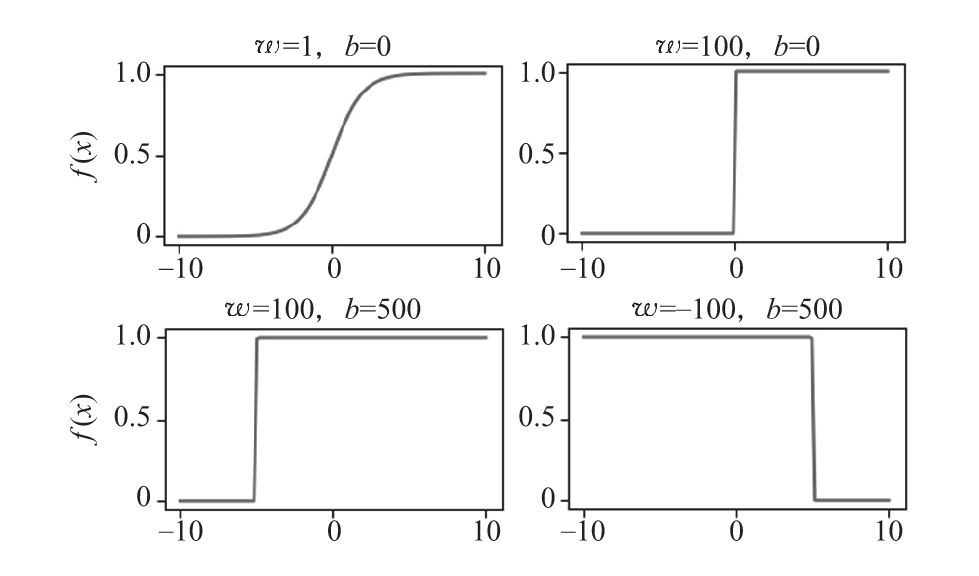
在不同的w和b值下的神經元輸出。網絡輸入x在x軸上表示
仔細檢查公式和圖,可以看到,sigmoid函數的陡度是由權重w決定的,函數在x軸上的平移是由公式t=-b/w決定的。我們討論一下上圖中的不同場景:
- 左上角的圖表顯示的是常規的sigmoid。
- 右上角的圖表顯示了一個較大的權值w將輸入x放大到一個點,在這個點上單元輸出類似于閾值激活。
- 左下角的圖表顯示了偏差b如何沿著x軸平移單元激活。
- 右下角的圖表顯示,我們可以以負權重w反轉激活,并沿具有偏差b的x軸轉換激活。
可以直觀地看到,前面的圖包含了方脈沖函數的所有成分。可以通過具有一個隱藏層的神經網絡將不同的場景結合起來,隱藏層包含上述兩個單元。下圖顯示了網絡架構、單元的權重和偏差,以及網絡產生的方脈沖函數:
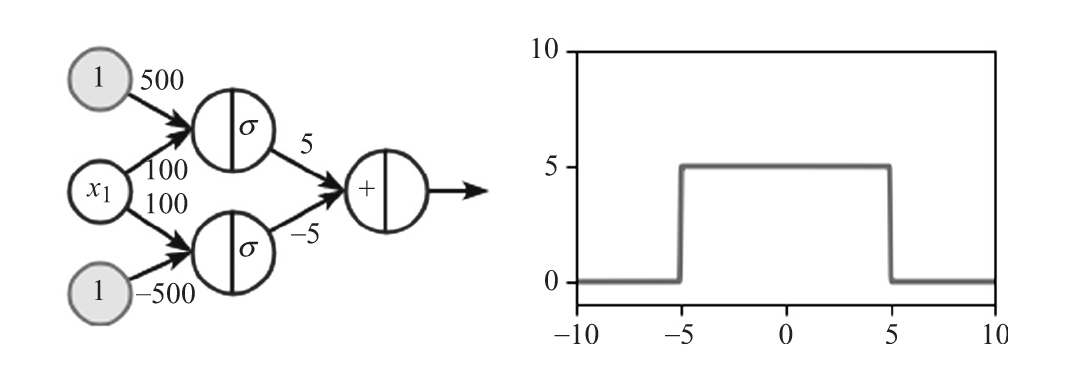
下面是它的工作原理:
- 首先,頂部單元激活函數的上部階梯激活并保持活躍。
- 底部單元隨后激活函數的底部階梯并保持活躍。由于輸出層的權重相同但符號相反,所以隱藏單元的輸出可以相互抵消。
- 輸出層的權重決定了方脈沖矩形的高度。
這個網絡的輸出不是0,而是在(-5,5)區間內。因此,可以用類似的方式在隱藏層中添加更多的單元來近似額外的方脈沖。
現在我們已經熟悉了神經網絡的結構,下面關注一下訓練過程。
- Learn TypeScript 3 by Building Web Applications
- 零基礎學C++程序設計
- 編寫高質量代碼:改善Python程序的91個建議
- 網店設計看這本就夠了
- Visual Basic學習手冊
- PySide GUI Application Development(Second Edition)
- Expert Data Visualization
- Mastering Drupal 8 Views
- NetBeans IDE 8 Cookbook
- 打開Go語言之門:入門、實戰與進階
- 深入剖析Java虛擬機:源碼剖析與實例詳解(基礎卷)
- SQL Server 2008 R2數據庫技術及應用(第3版)
- 創意UI Photoshop玩轉移動UI設計
- 趣學數據結構
- 深入淺出Go語言核心編程