2.2 系統模型描述

為控制輸出概率密度函數的形狀，對輸出概率密度函數用B樣條逼近。由于有理平方根B樣條模型綜合了平方根B樣條模型和有理B樣條模型的優點，因此這里用有理平方根B樣條[10]來逼近輸出概率密度函數。

記η（t）∈[a，b]為一致有界隨機過程并假定其為隨機系統在t時刻的輸出，并記u（t）為具有合適維數的控制η（t）分布的輸入向量。在任意時刻，η（t）的分布可以用它的條件PDFγ（y，u（t））來表述，其定義式如下。

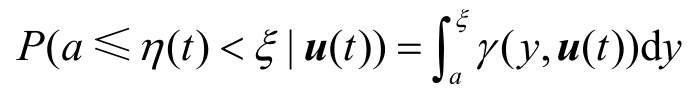
其中，P（a≤η（t）＜ξ|u（t））表示系統在u（t）作用下輸出y（t）落在區間[a，ξ）內的概率，即η（t）的PDFγ（y，u（t））的形狀可由u（t）控制。假設區間[a，b]已知，輸出PDFγ（y，u（t））連續且有界，由B樣條函數逼近原理可知[11]，可用以下有理平方根B樣條模型來逼近PDFγ（y，u（t））。

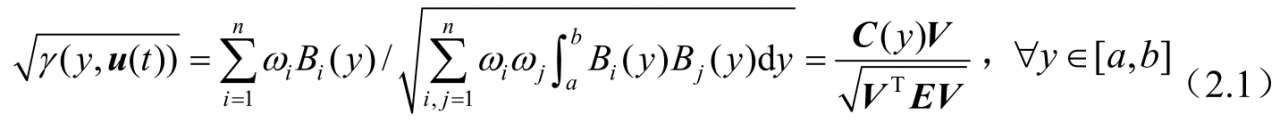
其中，Bi（y）≥0是預先指定的基函數；ωi是僅和控制輸入u（t）相關的逼近權值；n是基函數的個數；C（y）=[B1（y），B2（y），…，Bn（y）]，，V=[ω1，ω2，…，ωn]T且V≠0。

從式（2.1）可以看出，如果等式的右邊沒有分母，這個模型就是平方根B樣條模型；同時可以看出，式（2.1）在表達形式上十分類似于有理B樣條模型，故稱為有理平方根B樣條模型。需要指出的是：這里的n個權值ωi（i=1，2，…，n）是相互獨立的。因此，在這個表達式中不需要進一步的約束條件。

式（2.1）中的權值ωi（i=1，2，…，n）的意義與有理B樣條模型的權值相同，在這兩種情形中，當逼近PDF或PDF的平方根時，它們只是一個中間變量，且權值不唯一。這不同于線性和平方根B樣條模型的權值，線性和平方根B樣條模型的權值是真正的權值。對有理B樣條和有理平方根B樣條模型來說，它們真正的權值分別為和。然而，由B樣條神經網絡逼近原理[11]不難得出，真正的權值必須唯一，式中的ωi（i=1，2，…，n）為偽權值。偽權值是否唯一并不重要，重要的是目標函數能用這樣的B樣條函數來逼近，且在給定精度下逼近的真正的權值唯一。有理平方根B樣條模型綜合了平方根B樣條模型和有理B樣條模型的優點，其權值的可行域幾乎是整個區域。

假設由B樣條權值描述的系統動態部分能夠表示為線性連續定常系統，則這里所考慮的動態系統可表示為

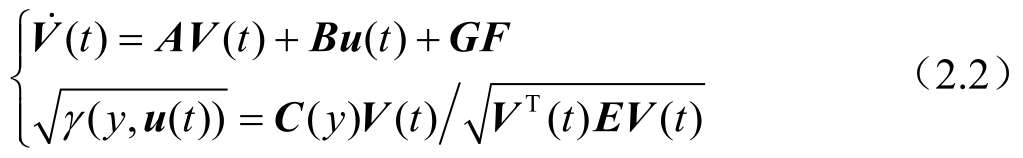
其中，u（t）為已知有合適維數的參數矩陣；F是一附加項，代表系統的故障。對該模型來說，第一個方程是關于V（t）、A、B、G、u（t）和F的一般線性動態關系式；第二個方程代表系統輸出概率密度函數的B樣條表達式。