- 計(jì)算機(jī)科學(xué)中的離散數(shù)學(xué)基礎(chǔ)
- (美)哈瑞·劉易斯 雷切爾·扎克斯
- 7665字
- 2025-08-07 15:17:29
第2章 基本證明技術(shù)
下面是用自然語言復(fù)述的鴿籠原理(見定理1.2):
如果鴿子比鴿籠多,并且每只鴿子都進(jìn)入一個(gè)鴿籠中,那么某個(gè)鴿籠中必裝有不止一只鴿子。
假設(shè)你的朋友不相信這個(gè)命題,你怎么能令人信服地論證這是真的呢?
你可能通過相反的結(jié)論不可能為真來試圖說服你的朋友。你可能說,讓我們想象一下,每個(gè)鴿籠中的鴿子不多于一只,然后計(jì)算一下鴿籠數(shù),因?yàn)槊總€(gè)鴿籠中有零只或一只鴿子,那么鴿子的數(shù)目最多等于鴿籠數(shù)。而開始時(shí)我們假設(shè)鴿子比鴿籠多,所以這是不可能的。由于每個(gè)鴿籠中最多有一只鴿子是不可能的,所以某個(gè)鴿籠中必裝有不止一只鴿子。這就是我們要試圖去證明的。
在這一章中,我們將討論如何將非規(guī)范、具體的論證,轉(zhuǎn)化為規(guī)范、泛化的數(shù)學(xué)證明。證明(proof)是一個(gè)論證過程:從一個(gè)或多個(gè)前提(例如,鴿子比鴿籠多)開始,使用邏輯規(guī)則推導(dǎo)出結(jié)論的過程(如有些鴿籠裝有不止一只鴿子)。盡管看上去用簡單的自然語言描述一個(gè)論證似乎更容易,但是自然語言不夠精確,也過于具體,用更規(guī)范的術(shù)語來描述數(shù)學(xué)問題會(huì)更為清晰,也更為泛化。
例2.1 下列命題的含義是什么?
每個(gè)人愛某個(gè)人
它的意思可以是:對(duì)于世界上的每一個(gè)人來說,都有一個(gè)他愛的人,即不同的人有不同的所愛。使用半數(shù)學(xué)語言,我們可以將這個(gè)語句表述為如下命題。
命題2.2 對(duì)于每個(gè)人A,都存在一個(gè)人B,使得A愛B。
對(duì)于例2.1還有另外一種解釋,即存在某個(gè)特別的人,每個(gè)人都愛他。
命題2.3 存在一個(gè)人B,對(duì)于每個(gè)人A,有A愛B。
這兩種解釋有很大的差別。數(shù)學(xué)語言的目的之一,就是解決自然語言的這種模糊性。
“對(duì)于所有的”“對(duì)于任意的”“對(duì)于每一個(gè)”“對(duì)于某些”以及“存在”,這些短語都被稱為量詞(quantifier),謹(jǐn)慎使用這些量詞是數(shù)學(xué)論述的重要組成部分。符號(hào)?代表“對(duì)于所有的”“對(duì)于任意的”“對(duì)于每一個(gè)”,符號(hào)?代表“存在”和“對(duì)于某些”。使用這些符號(hào)可以節(jié)省時(shí)間,但在數(shù)學(xué)短文中,它們也會(huì)使某些陳述變得更加難懂。因此,在第12章討論謂詞邏輯(quantificationallogic)的公式之前,我們避免使用量詞。
量詞是修飾謂詞(predicate)的,如A愛B。一個(gè)謂詞是一個(gè)命題模板,帶有一個(gè)或多個(gè)參數(shù),本例中是A和B。一個(gè)謂詞本身沒有真值,因?yàn)椴恢?i>A和B的值,所以“A愛B”既不能說是真的也不能說是假的,只有被量化后(如命題2.2和命題2.3所示)或者應(yīng)用了特定的參數(shù)(例如,羅密歐愛朱麗葉)后才有真值,并且可能對(duì)某些參數(shù)為真,而對(duì)另一些參數(shù)為假。
接下來給出數(shù)學(xué)命題及其證明的簡單示例。
定理2.4 奇數(shù)。任意奇數(shù)可表示為兩個(gè)整數(shù)的平方差。
首先,要確定我們真正理解了上述命題。一個(gè)奇(odd)數(shù)是可以寫成2k+1形式的任意整數(shù),其中k也是一個(gè)整數(shù)。整數(shù)n的平方(square)是n2=n·n。對(duì)于每一個(gè)k值,定理2.4的意思是存在兩個(gè)整數(shù)(稱為m和n),使得它們分別求平方后相減的結(jié)果等于2k+1。(注意其中的量詞:對(duì)于每個(gè)k,存在m和n,使得……)
如果一個(gè)整數(shù)m是某個(gè)整數(shù)的平方,則稱m為完全平方數(shù)(perfect square)。我們可以更簡潔地表述上述定理:任意奇數(shù)都可以表示為兩個(gè)完全平方數(shù)的差。數(shù)學(xué)中這種情況很典型,即定義一個(gè)恰當(dāng)?shù)母拍睿梢允箤?duì)普遍性事實(shí)的表述變得非常簡單。
下一步就是確認(rèn)為什么這個(gè)命題為真。如果理由不顯然,則用更多的例子會(huì)有所幫助。讓我們先列出前幾個(gè)平方數(shù):
02=0
12=1
22=4
32=9
42=16
我們可以確認(rèn),對(duì)于某些特定的奇數(shù),例如1、3、5和7,命題為真:
1=1-0=12-02
3=4-1=22-12
5=9-4=32-22
7=16-9=42-32
從上面這些例子,我們注意到一個(gè)規(guī)律,即所有列出的奇數(shù)都是兩個(gè)連續(xù)整數(shù)的平方差,這些整數(shù)是0和1、1和2、2和3,以及3和4。另外觀察到這些連續(xù)整數(shù)相加分別得到了與上面相同的奇數(shù):0+1=1、1+2=3、2+3=5、3+4=7。因此,我們可以推測:奇數(shù)2k+1應(yīng)該是k+1與k的平方差。我們來試一下:
(k+1)2-k2=k2+2k+1-k2
化簡后得到2k+1。
我們猜對(duì)了!我們定義奇數(shù)為2k+1,從而沒有用特定的奇數(shù),就確認(rèn)了定理2.4適用于所有奇數(shù)。它甚至也適用于負(fù)奇數(shù)(2k+1中的k為負(fù)值),盡管這個(gè)思想是通過正奇數(shù)示例得到的。
上面一系列的思考雖然展示了定理的思想是怎樣得到的,但是作為一個(gè)規(guī)范的證明依然過于煩瑣,實(shí)質(zhì)性證明應(yīng)該僅包括相關(guān)的細(xì)節(jié)。例如,所列出的例子不能加在論據(jù)中,即我們需要證明任何情況下命題都為真,而不僅僅是對(duì)列出的例子為真。下面是定理2.4的一個(gè)規(guī)范證明。
證明:對(duì)于任意奇數(shù)2k+1(其中k為整數(shù))都有
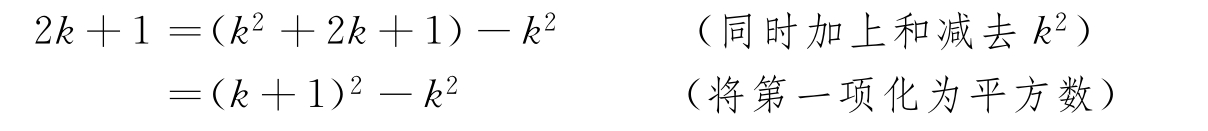
令m=k+1、n=k,那么有2k+1=m2-n2,我們找到了具有前面所述性質(zhì)的整數(shù)m和n。■
在驗(yàn)證這個(gè)證明的本質(zhì)之前,先就其風(fēng)格做進(jìn)一步說明。第一,它用完整的語句寫成,數(shù)學(xué)表達(dá)式使表述更精確和清晰,而論斷過程是用短文形式表達(dá)的。第二,它的結(jié)構(gòu)是清晰的:從已知假設(shè)開始(某整數(shù)是奇數(shù)),通過指明m和n是我們所尋求的兩個(gè)整數(shù),清晰地給出了證明的結(jié)尾。第三,它是嚴(yán)格的:給出了相關(guān)術(shù)語(奇數(shù))的數(shù)學(xué)定義,該定義使我們的推證更細(xì)致和清晰,此外證明過程中的每一步都是由前面若干步邏輯清晰地推得的。
它還是令人信服的。該證明提供了充分的細(xì)節(jié),讓讀者容易理解為什么每一步都是正確的,但又免于煩瑣。例如,我們跳過了某些算術(shù)運(yùn)算步驟,只表明了
2k+1=(k+1)2-k2
這個(gè)等式并不直觀,細(xì)心的讀者可能會(huì)帶著質(zhì)疑去驗(yàn)證它。當(dāng)我們給出了中間步驟,運(yùn)算結(jié)果顯然是正確的。有些假設(shè)不需要證明,例如,下面的步驟就是有效的
2k+1=(k2+2k+1)-k2
事實(shí)上,不管我們?cè)鯓右祈?xiàng)、合并同類項(xiàng),它們的和是不變的。在這段內(nèi)容中,這些規(guī)則看似相當(dāng)基本,但是可以用作假設(shè)。證明這些規(guī)則會(huì)分散讀者對(duì)主要論斷的注意力。但在有關(guān)規(guī)范的算術(shù)運(yùn)算的教材中,這些性質(zhì)本身就是一個(gè)證明的主題。要包含多少細(xì)節(jié)取決于內(nèi)容和目標(biāo)讀者。
現(xiàn)在回到上述證明的本質(zhì)。首先,它是構(gòu)造性的(constructive)。要證明的命題僅斷言了某些事物的存在:對(duì)于任何奇數(shù),存在兩個(gè)整數(shù),它們的平方差等于該奇數(shù)。一個(gè)構(gòu)造性的證明不僅可以證明這個(gè)事物是存在的,還可以展示如何找到它。已知某個(gè)特定的奇數(shù)2k+1,定理2.4的證明向我們展示了如何找到兩個(gè)整數(shù)具有命題中所斷言的性質(zhì):一個(gè)是k+1,另一個(gè)是k。例如,如果我們想要表達(dá)的奇數(shù)是341,按照上述證明的方法,我們可以從341中減去1再除以2,該整數(shù)和下一個(gè)更大的整數(shù)就是所尋找的整數(shù)對(duì),即170和171。驗(yàn)證很容易:
1712-1702=29241-28900=341
其實(shí)沒必要去驗(yàn)證這種特定的情況,之所以這樣做,只是讓我們更確信代數(shù)運(yùn)算沒有錯(cuò)誤。
一般來說,回答問題或解決問題的過程被稱為算法(algorithm)。算法的描述足夠詳細(xì)和精確,原則上說,它是可機(jī)械執(zhí)行的,既可以在機(jī)器上運(yùn)行,也可以由人按照指令進(jìn)行運(yùn)算并不加以思考。一個(gè)構(gòu)造性的證明本質(zhì)上就是一個(gè)尋找證明中存在的事物的算法。在定理2.4中,證明描述的算法是:已知一個(gè)奇數(shù)2k+1,尋找整數(shù)m和n,使得m2-n2=2k+1。
并非每一個(gè)證明都是構(gòu)造性的,有的僅證明了存在性而沒有給出如何尋找的方法。這樣的證明被稱為非構(gòu)造性的(nonconstructive)。我們將看到一些有趣的非構(gòu)造性證明的例子。事實(shí)上,鴿籠原理的證明就是非構(gòu)造性的,因?yàn)樗鼰o法識(shí)別哪個(gè)鴿籠中有一只以上的鴿子。然而計(jì)算機(jī)科學(xué)家們喜歡構(gòu)造性論證,因?yàn)橐粋€(gè)構(gòu)造性的證明會(huì)生成一個(gè)可尋找所存在事物的算法,此算法能夠編程實(shí)現(xiàn)并在計(jì)算機(jī)上運(yùn)行[1]。
有關(guān)定理2.4的最后一個(gè)說明是它的證明不僅具有構(gòu)造性,而且包含超出了原有結(jié)論的其他結(jié)論。定理2.4不僅證明了每個(gè)奇數(shù)是兩個(gè)整數(shù)的平方差,而且證明了是兩個(gè)連續(xù)整數(shù)(constructive integers)的平方差(參見該定理證明)。完成一個(gè)證明后,值得回顧一下,看看是否會(huì)產(chǎn)生命題之外的有趣結(jié)論。
數(shù)學(xué)證明的基本目標(biāo)是確定兩個(gè)命題之間的等價(jià)性,即命題一在命題二為真的所有情況下都為真,反之亦然。例如,下面的命題:
一個(gè)整數(shù)的平方是奇數(shù),當(dāng)且僅當(dāng)該整數(shù)本身是奇數(shù)。
或者,用常規(guī)的數(shù)學(xué)風(fēng)格可以表示為如下定理。
定理2.5 對(duì)于任意的整數(shù)n,n2是奇數(shù)當(dāng)且僅當(dāng)n是奇數(shù)。
這是一個(gè)非常典型的數(shù)學(xué)命題,有以下幾點(diǎn)值得注意。
? 它使用了變量n來指代所討論的事物,因此可以用該名稱在命題的其他部分來指代同一事物。
? 按照慣例,使用名稱n表示整數(shù)。其他的名稱,比如x,表示一個(gè)任意的實(shí)數(shù);p表示一個(gè)質(zhì)數(shù)。盡管變量名稱的選擇與數(shù)學(xué)意義不相關(guān),但是使用慣例命名變量名稱有助于讀者對(duì)命題的理解。
? 雖然變量名稱是遵循慣例的,但是命題并不完全依賴變量名稱的慣例含義。特別指出:n代表一個(gè)整數(shù),所以根據(jù)上下文,n也可以是正整數(shù)、非負(fù)整數(shù)或其他類型的數(shù)等。
? 命題使用了一個(gè)量詞(對(duì)于任意的),這是為了明確所描述的性質(zhì)適用于所有整數(shù)。
? 命題“n2是奇數(shù)當(dāng)且僅當(dāng)n是奇數(shù)”實(shí)際上是將兩個(gè)命題合二為一:
1.“n2是奇數(shù)當(dāng)n是奇數(shù)”,或?yàn)椤叭绻?i>n是奇數(shù),那么n2是奇數(shù)”;
2.“n2是奇數(shù)僅當(dāng)n是奇數(shù)”,或?yàn)椤叭绻?i>n2是奇數(shù),那么n是奇數(shù)”。
讓我們來定義“當(dāng)且僅當(dāng)”命題的兩個(gè)原子命題:p表示n2是奇數(shù),q表示n是奇數(shù)。思考一下“僅當(dāng)”的含義:“p僅當(dāng)q”與“如果p,那么q”具有相同的含義:如果我們知道p為真,那么q的唯一可能也為真。
一個(gè)“當(dāng)且僅當(dāng)”命題為真,只有在兩個(gè)原子命題“p當(dāng)q”和“p僅當(dāng)q”都為真的情況下成立,或者說,只有在兩個(gè)原子命題p和q等價(jià)的情況下成立。短語“當(dāng)且僅當(dāng)”通常縮寫為iff。
證明兩個(gè)命題的等價(jià)性通常由兩個(gè)證明步驟組成:證明每個(gè)命題都蘊(yùn)含另一個(gè)命題。例如,在定理2.5中,我們證明了如果一個(gè)整數(shù)是奇數(shù),那么它的平方也是奇數(shù),然后我們證明了如果一個(gè)整數(shù)的平方是奇數(shù),那么這個(gè)整數(shù)本身就是奇數(shù)。一般來說,兩個(gè)方向的證明看上去非常不同。無論有多困難,在兩個(gè)方向都得到證明之前,等價(jià)性證明都是不完整的。
定理2.5的第一個(gè)方向(如果n是奇數(shù),那么n2是奇數(shù))可以采用直接證明法(direct proof)來證明。這類證明方法是直截了當(dāng)?shù)模杭僭O(shè)前提是真的,然后從前提證明結(jié)論是真的。對(duì)于第二個(gè)方向(如果n2是奇數(shù),那么n是奇數(shù)),從稍微不同的角度來思考,會(huì)更容易些。直接的證明是假設(shè)n2是奇數(shù),由此去證明n是奇數(shù),但似乎沒有簡單的方法可以做到這一點(diǎn)。代之以等價(jià)的證明:若n不是奇數(shù),即n是偶數(shù),那么n2也不是奇數(shù)。
證明等價(jià)性
要證明“p當(dāng)且僅當(dāng)q”:證明“p當(dāng)q”,即“如果q,那么p”;證明“p僅當(dāng)q”,即“如果p,那么q”。
證明:首先,我們證明如果n是奇數(shù),那么n2是奇數(shù)。如果n是奇數(shù),那么可以表示為:n=2k+1,其中k是整數(shù)。則有

設(shè)j為整數(shù)2k2+2k,則n2=2j+1,所以n2是奇數(shù)。
接下來,我們證明如果n2是奇數(shù),那么n是奇數(shù)。假設(shè)這不是對(duì)所有的n都成立,那么存在某個(gè)整數(shù)n,使得n2是奇數(shù),而n不是奇數(shù)。因?yàn)槿魏握麛?shù)若不是奇數(shù),必定為偶數(shù),所以n為偶數(shù)。為了證明這樣的n不存在,我們需要證明“如果n是任意偶數(shù),那么n2是偶數(shù)”。此時(shí),n是偶數(shù),則設(shè)n=2k,其中k是整數(shù)。則有

設(shè)j為整數(shù)2k2,則n2=2j,所以n2是偶數(shù),也就是假設(shè)(n是一個(gè)整數(shù),使得n2是奇數(shù),但n不是奇數(shù))是假的。所以它的否定命題是真的,即如果n2是奇數(shù),那么n是奇數(shù)。■
這個(gè)證明比定理2.4的證明步驟更多一些,也更結(jié)構(gòu)化一些。在一個(gè)比較長的證明中,要將多個(gè)步驟有條理地結(jié)合在一起,從而使讀者不僅明白單獨(dú)一個(gè)步驟的作用,還能理解論點(diǎn)的整體思想。例如,為了引導(dǎo)讀者理解這個(gè)證明,我們?cè)趯?duì)論點(diǎn)的每個(gè)部分深入證明之前,都表明了證明的方向。
更復(fù)雜的證明可能有多個(gè)中間步驟。當(dāng)一個(gè)中間步驟特別長或者很難的時(shí)候,可以先將這個(gè)中間步驟獨(dú)立出來,從而使整個(gè)證明不會(huì)太長。中間步驟本身也可以是一個(gè)定理,如果它與要證明的定理在內(nèi)容上不是特別相關(guān),我們稱之為引理(lemma)。另外,定理得到證明之后,會(huì)帶來一些更容易證明的相關(guān)結(jié)論,我們稱其為定理的推論(corollary),而不是“定理的定理”。例如,下面是定理2.5的推論:
推論2.6 如果n是奇數(shù),那么n4是奇數(shù)。
證明:注意n4=(n2)2,由于n是奇數(shù),根據(jù)定理2.5,n2是奇數(shù)。又由于n2是奇數(shù),再次根據(jù)定理2.5,有n4是奇數(shù)。■
在定理2.5證明的第二部分,我們采用了蘊(yùn)含(implication)推理,即把形如“如果p,那么q”的命題,轉(zhuǎn)化為等價(jià)的“如果非q,那么非p”。在證明的這一部分中,p表示n2是奇數(shù),q表示n是奇數(shù)。蘊(yùn)含命題有多種變體,對(duì)這些變體的命名和辨別很重要[2]。
對(duì)蘊(yùn)含命題“如果p,那么q”有三種不同的翻轉(zhuǎn)方式。將其中的兩個(gè)部分做否定就得到了反換式(inverse)命題“如果非p,那么非q”;僅改變其中兩部分的順序,可得到逆換式(converse)命題“如果q,那么p”;既改變兩部分的順序又做否定可得到逆反式(contrapositive)命題“如果非q,那么非p”。
因?yàn)槊}的逆反式與該命題邏輯等價(jià),所以可以通過其中一個(gè)命題的證明來證明另一個(gè),如同反證法的邏輯一樣。這就是為什么我們可以用“如果n是奇數(shù),那么n2是奇數(shù)”的證明,來代替“如果n2是奇數(shù),那么n是奇數(shù)”的證明,它們互為逆反式。
注意:反換式和逆換式與原命題不等價(jià)。例如,在上述證明中,必須包含“如果n是奇數(shù),那么n2是奇數(shù)”和“如果n2是奇數(shù),那么n是奇數(shù)”這兩個(gè)命題的證明,因?yàn)檫@兩個(gè)命題互為逆換式,邏輯不等價(jià)。
我們使用了命題的另一種變體。命題p的否定(negation)也是命題:p為假。換句話說,是命題“非p”。因此,“n是奇數(shù)”的否定命題是“n是偶數(shù)”。“如果p,那么q”的逆反式是“如果非q,那么非p”。
命題的變體
s=如果p,那么q
q當(dāng)p(等價(jià)于s)
p僅當(dāng)q(等價(jià)于s)
逆反式:
如果非q,那么非p(等價(jià)于s)。
反換式:
如果非p,那么非q(不等價(jià)于s)。
逆換式:
如果q,那么p(不等價(jià)于s,它是反換式的逆反式,因此等價(jià)于反換式)。
數(shù)學(xué)語言表達(dá)思想更廣泛、更精確,但是高度的抽象也會(huì)造成混亂。當(dāng)使用這種方式表達(dá)思想時(shí),必須格外小心,確保我們所得到的命題是有意義的。我們?cè)谝粋€(gè)證明中要保持質(zhì)疑,使得每一步都必須由前面某一步或若干步的結(jié)果推導(dǎo)而得。例如,下面對(duì)1=2的偽證明:
令a=b,那么有

哪里出錯(cuò)了呢?顯然我們得到的結(jié)論是不成立的,開始的假設(shè)(a=b)是成立的,所以必定在證明的某一步上,我們犯了邏輯錯(cuò)誤。
錯(cuò)誤發(fā)生在第三步到第四步的時(shí)候。我們開始時(shí)假設(shè)a=b,所以除以a-b實(shí)際上是除以零,這不是有效的算術(shù)運(yùn)算。因此,在這一步上出現(xiàn)了邏輯錯(cuò)誤,后面都是無意義的了。在做證明時(shí),務(wù)必牢記符號(hào)的意義,以避免類似的錯(cuò)誤。
對(duì)2=1的偽證明看上去像證明但實(shí)際上不是證明。因?yàn)槌霈F(xiàn)了不成立的結(jié)論,所以我們意識(shí)到一定在某個(gè)步驟上出現(xiàn)了錯(cuò)誤,這迫使我們回溯論證,去找出出錯(cuò)的地方。這種推理方式(推導(dǎo)出矛盾,意味著論點(diǎn)有錯(cuò)誤)實(shí)際上是一種非常有用的證明技術(shù)。事實(shí)上,在定理2.5第二部分的證明中,我們已經(jīng)看到了反證法的例子。
反證法從假設(shè)命題的否定成立開始,如果我們能夠推導(dǎo)出一個(gè)矛盾(整個(gè)過程沒有任何邏輯錯(cuò)誤),那么唯一的可能就是論證開始的假設(shè)出了問題。由于假設(shè)命題的否定成立而導(dǎo)致了矛盾,因此確定命題為真。
反證法
通過產(chǎn)生矛盾來證明p,即假設(shè)p是假的,推導(dǎo)出矛盾的結(jié)果,得到結(jié)論:p必為真。
我們?cè)倏戳硪粋€(gè)例子,使用反證法來證明![]() 是無理數(shù)。按照慣例,首先要正確理解命題的含義。一個(gè)有理數(shù)(rational number)可以表示為兩個(gè)整數(shù)之比。例如,1.25是有理數(shù),因?yàn)樗梢员硎緸?img alt="" height="49" src="https://epubservercos.yuewen.com/3F3CAA/33385066407508506/epubprivate/OEBPS/Images/22_02.jpg?sign=1755908194-ALBwUDsU5FG2aXiHHRRepmNnHg86qorM-0-fdf76f618c44e49d32bc9db9daf28825" style="vertical-align:middle" width="26">(或者
是無理數(shù)。按照慣例,首先要正確理解命題的含義。一個(gè)有理數(shù)(rational number)可以表示為兩個(gè)整數(shù)之比。例如,1.25是有理數(shù),因?yàn)樗梢员硎緸?img alt="" height="49" src="https://epubservercos.yuewen.com/3F3CAA/33385066407508506/epubprivate/OEBPS/Images/22_02.jpg?sign=1755908194-ALBwUDsU5FG2aXiHHRRepmNnHg86qorM-0-fdf76f618c44e49d32bc9db9daf28825" style="vertical-align:middle" width="26">(或者![]() ,還有更多的方式)。如果一個(gè)數(shù)不是有理數(shù),那么它就是無理數(shù)(irrational number),即不能表示為兩個(gè)整數(shù)之比的數(shù)。
,還有更多的方式)。如果一個(gè)數(shù)不是有理數(shù),那么它就是無理數(shù)(irrational number),即不能表示為兩個(gè)整數(shù)之比的數(shù)。
我們?cè)噲D直接證明![]() 是無理數(shù),但是完全不清楚應(yīng)該如何進(jìn)行(甚至不知道從哪里開始)。因此,我們想到如果這個(gè)命題不是真的,會(huì)發(fā)生什么,假設(shè)的結(jié)果是否會(huì)產(chǎn)生邏輯上的矛盾。
是無理數(shù),但是完全不清楚應(yīng)該如何進(jìn)行(甚至不知道從哪里開始)。因此,我們想到如果這個(gè)命題不是真的,會(huì)發(fā)生什么,假設(shè)的結(jié)果是否會(huì)產(chǎn)生邏輯上的矛盾。
定理2.7 ![]() 是無理數(shù)。
是無理數(shù)。
證明:為了推導(dǎo)矛盾,假設(shè)命題是假的,即![]() 不是無理數(shù)。這意味著
不是無理數(shù)。這意味著![]() 是有理數(shù),換句話說,可表示為兩個(gè)整數(shù)的比。因此,假設(shè)
是有理數(shù),換句話說,可表示為兩個(gè)整數(shù)的比。因此,假設(shè)![]() ,a和b為整數(shù),其中a和b最多有一個(gè)是偶數(shù)(這個(gè)附加的假設(shè)是可行的,因?yàn)槿绻麅烧叨际桥紨?shù),我們可以通過分別除以2得到等值的分?jǐn)?shù),從而有更小的分子和分母):
,a和b為整數(shù),其中a和b最多有一個(gè)是偶數(shù)(這個(gè)附加的假設(shè)是可行的,因?yàn)槿绻麅烧叨际桥紨?shù),我們可以通過分別除以2得到等值的分?jǐn)?shù),從而有更小的分子和分母):
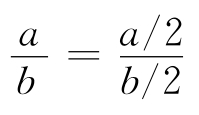
重復(fù)以上操作,直到得到分子或分母(或全部)為奇數(shù)的分?jǐn)?shù)。因此,可以不失一般性[3](without loss of generality)地假設(shè)![]() ,并且a、b中至少有一個(gè)奇數(shù)。由于
,并且a、b中至少有一個(gè)奇數(shù)。由于![]() ,將兩端乘以b,可得
,將兩端乘以b,可得![]() 。將等式兩端取平方,可得
。將等式兩端取平方,可得
所以a2可以被2整除。也就是說,a2不是奇數(shù),根據(jù)定理2.5,a也不是奇數(shù),換句話說,a可以被2整除。因此,設(shè)a=2k,其中k是整數(shù),于是式(2-8)變成
2b2=(2k)2=4k2
兩端除以2,得到b2=2k2。因此,b2是偶數(shù),從而b必定是偶數(shù)。我們證明了a和b都是偶數(shù),這與假設(shè)“a和b中最多有一個(gè)偶數(shù)”相矛盾。所以,![]() 必定是無理數(shù),得證。■
必定是無理數(shù),得證。■
有時(shí)要證明的命題可以被劃分為若干塊,每一塊可以被單獨(dú)證明,這些塊組合起來就能構(gòu)成完整的論點(diǎn),這時(shí)證明就變得更容易了。在定理2.5的證明中就采用了這種簡單的方法,我們將“當(dāng)且僅當(dāng)”命題劃分為兩個(gè)蘊(yùn)含命題,然后分別做了證明。采用這種思想的另一種證明方法叫作情況分析(case analysis),它是將有關(guān)一個(gè)類的總命題劃分為若干子類相關(guān)的命題。如果對(duì)于每一種可能的情況,命題都會(huì)得到證明,那么總的原始命題必定為真。在定理1.8中我們看到了一個(gè)簡單的情況分析,其中,我們?cè)噲D找到一個(gè)大于前k個(gè)質(zhì)數(shù)p1,…,pk的質(zhì)數(shù),并且推斷(p1·p2·…·pk)+1要么是質(zhì)數(shù),要么具有一個(gè)比任何pi都大的質(zhì)因子,每一種可能都證明了相應(yīng)的結(jié)論。下面的例題應(yīng)用了更復(fù)雜的情況分析。
例2.9 證明在任意六人群中,有3人相互認(rèn)識(shí),或者有3人相互陌生。(“認(rèn)識(shí)”是對(duì)稱的,即如果A認(rèn)識(shí)B,那么B也認(rèn)識(shí)A。)[4]
解:首先從6個(gè)人中任意選出一個(gè)人X。在剩下的5個(gè)人中,至少有3個(gè)人是X認(rèn)識(shí)的,或者至少有3個(gè)人是X不認(rèn)識(shí)的(見習(xí)題2.15)。依據(jù)每種情況為真,論證分為兩種主要情況,每種主要情況又分為兩種子情況。
情況1.X至少認(rèn)識(shí)3個(gè)人。那么再來看一下這3個(gè)人之間的關(guān)系。如果他們中的任意2個(gè)人彼此都不認(rèn)識(shí),那么這3個(gè)人相互都是陌生的。如果其中有某2個(gè)人相互認(rèn)識(shí),那么這兩個(gè)人再加上X就構(gòu)成了一組互相認(rèn)識(shí)的3個(gè)人。
情況2.至少有3個(gè)人X不認(rèn)識(shí)。考慮一下X不認(rèn)識(shí)的這3個(gè)人。如果這3個(gè)人互相認(rèn)識(shí),他們就組成了一組互相認(rèn)識(shí)的3個(gè)人。否則,他們中至少有2個(gè)人彼此不認(rèn)識(shí),這2個(gè)人加上X,就構(gòu)成了一組相互不認(rèn)識(shí)的3個(gè)人。■
在這個(gè)證明中,情況2中的論證似乎很像情況1中的論證,只是互換了“認(rèn)識(shí)”和“不認(rèn)識(shí)”的角色。事實(shí)上,除了角色互換之外,這兩個(gè)論證是完全相同的。這個(gè)例子展示了另一種常用的證明技術(shù):對(duì)稱性(symmetry)。
論證中的對(duì)稱性如圖2.1所示,我們將在第16~18章中深入討論這種圖。A,B,…,F代表6個(gè)人,黑色線連接的兩個(gè)人彼此認(rèn)識(shí),灰色線連接的兩人相互不認(rèn)識(shí)。因此,情況1是指當(dāng)選定某個(gè)人X(如圖中的E)時(shí),他認(rèn)識(shí)(通過黑色線連接的)其他3個(gè)人。情況2是指當(dāng)選定某個(gè)人X(如圖中的A)時(shí),他不認(rèn)識(shí)(通過灰色線連接的)其他3個(gè)人。除了互換黑、灰兩種顏色之外,論證完全是對(duì)稱的。我們可以說,在有6個(gè)節(jié)點(diǎn)的圖中,每對(duì)節(jié)點(diǎn)之間都有邊相連,如果邊是兩種顏色中的一種,則圖中包含一個(gè)同色(單色)的三角形。(圖2.1中E、B和D構(gòu)成一個(gè)這樣的三角形)。
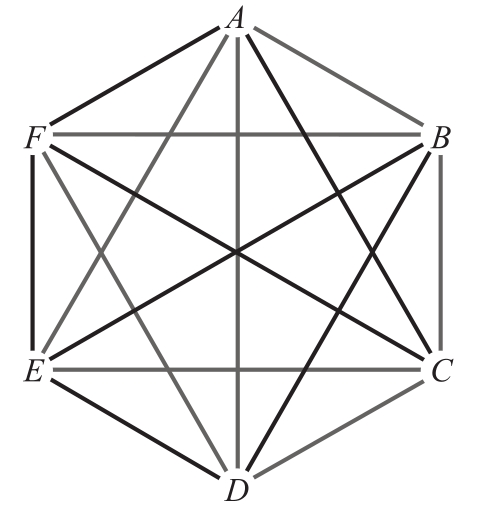
圖2.1 一張圖展示了6個(gè)人之間的關(guān)系,黑色線連接著彼此認(rèn)識(shí)的人,灰色線連接著相互不認(rèn)識(shí)的人
一旦確定了對(duì)稱性,就不需要給出兩次相同的論證。在情況2中,我們只需要表述“如果至少有3個(gè)人與X不認(rèn)識(shí),那么這個(gè)論證是對(duì)稱的,即互換了‘認(rèn)識(shí)’與‘不認(rèn)識(shí)’的角色”。一個(gè)存在對(duì)稱性的論證比沒有發(fā)現(xiàn)對(duì)稱性的論證更短且更能揭示本質(zhì)。在確定了對(duì)稱性的情況下,結(jié)果的陳述變得更簡單,因?yàn)橥切慰梢员硎?個(gè)人彼此認(rèn)識(shí)也可以表示3個(gè)人相互不認(rèn)識(shí)。
- 數(shù)字經(jīng)濟(jì):“數(shù)字中國”頂層規(guī)劃與實(shí)踐路徑
- 粵港澳大灣區(qū)觀察:帶你看清大灣區(qū)八大產(chǎn)業(yè)發(fā)展前景(《21世紀(jì)經(jīng)濟(jì)報(bào)道》深度觀察)
- 魔鬼數(shù)學(xué):大數(shù)據(jù)時(shí)代,數(shù)學(xué)思維的力量
- 數(shù)量經(jīng)濟(jì)研究(2018年/第9卷/第2期)
- 穿透數(shù)據(jù):經(jīng)濟(jì)數(shù)據(jù)理解要點(diǎn)與分析應(yīng)用(職業(yè)教育經(jīng)濟(jì)管理類新形態(tài)系列教材)
- 此算與彼算:圓錐曲線在清代
- 統(tǒng)計(jì)學(xué)
- 算力:數(shù)字經(jīng)濟(jì)的新引擎
- 數(shù)量經(jīng)濟(jì)研究(2017年/第8卷/第2期)
- 數(shù)量經(jīng)濟(jì)研究(2016年/第7卷/第2期)
- 定性數(shù)據(jù)的統(tǒng)計(jì)分析
- 數(shù)學(xué)史講義概要
- 數(shù)量經(jīng)濟(jì)研究(2016年/第7卷/第1期)
- 走向數(shù)字經(jīng)濟(jì)
- 數(shù)量經(jīng)濟(jì)研究(2019年/第10卷/第1期)