- 計算機科學(xué)中的離散數(shù)學(xué)基礎(chǔ)
- (美)哈瑞·劉易斯 雷切爾·扎克斯
- 4954字
- 2025-08-07 15:17:28
第1章 鴿籠原理
我們?nèi)绾沃酪欢斡嬎銠C程序能產(chǎn)生正確的結(jié)果?我們又如何知道一段程序能完整運行?如果我們知道它必然會停下來,那么能預(yù)測停止時間是一秒之后、一小時之后還是一天之后嗎?直覺地想道:測試。但即使“每一次測試都正常”也不能成為上述問題的嚴格證明。證明一個論斷需要規(guī)范的推證過程:從已知為真的一些命題出發(fā),并通過嚴謹?shù)倪壿嬐评韺⑦@些為真的命題連接到一起。本書的目的就是闡述能夠用來推證有關(guān)上述計算機程序行為的數(shù)學(xué)。
計算機科學(xué)數(shù)學(xué)并非什么特殊的領(lǐng)域,而是計算機科學(xué)家們所用到的各個數(shù)學(xué)分支中的相關(guān)內(nèi)容的匯集,甚至有些內(nèi)容是在計算機科學(xué)發(fā)展過程中首次發(fā)現(xiàn)了其應(yīng)用價值。因此,這本書包括的內(nèi)容涉及數(shù)理邏輯、圖論、計數(shù)、數(shù)論和離散概率論等。從傳統(tǒng)數(shù)學(xué)課程的角度來看,這些內(nèi)容相互之間有些風(fēng)馬牛不相及,但它們擁有一個共同的特征:在計算機科學(xué)中都有重要的作用,并且都屬于離散數(shù)學(xué)(discrete mathematics),也就是說,所涉及的量相互之間是有距離而不是連續(xù)的,量可以用符號或者結(jié)構(gòu)(而非數(shù)字)來表示。當(dāng)然,微積分學(xué)在計算機科學(xué)中也很重要,因為它有助于連續(xù)量的推證。但在本書中,我們很少使用積分和求導(dǎo)數(shù)。
數(shù)學(xué)思維最重要的技能之一就是泛化(generalization)。例如,下述命題:
不存在邊長分別為1、2和6的三角形
為真,且這個命題非常具體(見圖1.1)。長度為1和2的兩條邊必須分別與長度為6的邊的兩端相連,但這兩條短邊的總長度不足以使它們相連構(gòu)成第三個角。
更為泛化的陳述可以是(見圖1.2):
不存在邊長為a、b、c的三角形,其中a、b、c是任意的,且滿足a+b≤c。
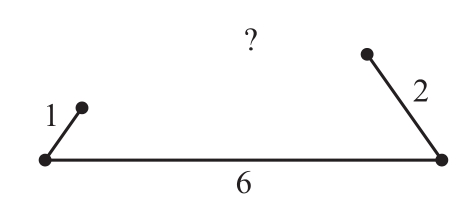
圖1.1 存在一個邊長為1、2和6的三角形嗎
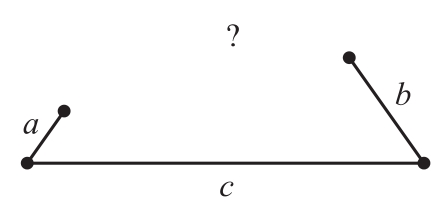
圖1.2 不存在邊長為a、b、c的三角形,如果a+b≤c
第二種形式更為泛化,因為可以通過代入a=1、b=2、c=6來推導(dǎo)出第一種形式。它也涵蓋了圖中沒有展示的情況,即當(dāng)a+b=c時,三個角落在一條直線上的情況。總之,泛化規(guī)則具有優(yōu)勢,它不僅陳述了不可能的情況,而且給出了相應(yīng)的解釋,例如,不存在邊長為1、2和6的三角形,因為1+2≤6。
因此,我們以泛化的形式表述命題有兩個理由。首先,一個命題越泛化則越易于應(yīng)用,并且應(yīng)用范圍更廣泛。其次,對一個泛化的命題更易于捕捉其要點,因為它剔除了不相關(guān)且贅述的細節(jié)。
例1.1 再來看另一個簡單的例子:
Annie、Batul、Charlie、Deja、Evelyn、Fawwaz、Gregoire和Hoon在互相交談時,發(fā)現(xiàn)Deja和Gregoire都是星期二出生的。
什么意思呢?當(dāng)把兩個人放在一起時,他們要么在一周內(nèi)的同一天出生,要么不在。這里能進行泛化。只要至少有八個人,其中就一定有某兩個人是在一周的同一天出生的,因為一周只有七天。像例1.1這樣的命題一定是真的,只是可能涉及不同的一對名字和不同的一天。所以更泛化的命題如下:
任意八個人中,某兩個人一定是在一周的同一天出生的。
但是,上面的命題泛化得還不夠。因為,生日重疊在同一天與什么人和星期幾無關(guān),只與有多少人和一周中有多少天相關(guān)。同樣的情況:當(dāng)我們把八個茶杯放在七個茶托上時,某個茶托上會放有兩個茶杯。事實上,“八”和“七”并沒有什么神奇之處,只是其中一個比另一個大。如果一家酒店有1000個房間和1001位客人,某個房間必然至少有兩位客人。如何去陳述上述所有示例的基本原理,而又不提及其中任何不相關(guān)的細節(jié)呢?
首先,我們需要一個新的概念:集合(set)是一些事物或元素(element)的匯集。屬于集合的元素稱為集合的成員(member)。一個集合的成員是可區(qū)分的(distinct),換句話說,它們彼此是不相同的。于是,例1.1中提到的人構(gòu)成一個集合,一周中的星期幾構(gòu)成另一個集合。有時我們顯式地列出集合的所有成員,用花括號{}將它們括起來:
P={Annie,Batul,Charlie,Deja,Evelyn,Fawwaz,Gregoire,Hoon}
D={星期一,星期二,星期三,星期四,星期五,星期六,星期日}
當(dāng)列出一個集合的所有元素時,元素的順序無關(guān)緊要——任何順序都表示同樣的集合。我們用x∈X來表示x是集合X的成員。例如,Charlie∈P,星期四∈D。
為了討論集合,需要有關(guān)數(shù)的一些基本術(shù)語。整數(shù)(integer)是指數(shù)字0、1、2、…,或-1、-2…。實數(shù)是數(shù)軸上的所有數(shù),包括整數(shù)以及整數(shù)之間的所有數(shù),如![]() 、π等。大于0的數(shù)為正數(shù),小于0的數(shù)為負數(shù),大于或等于0的數(shù)為非負整數(shù)。
、π等。大于0的數(shù)為正數(shù),小于0的數(shù)為負數(shù),大于或等于0的數(shù)為非負整數(shù)。
接下來,我們將討論有窮集,也稱有限集。有窮集是可以(至少原則上)列出其全部元素的集合,具有為非負整數(shù)的大小(size)或基數(shù)(cardinality)。集合X的基數(shù)表示為|X|。例如,在上述例子中,有|P|=8和|D|=7。因為列出了八個人,并且一周中有七天。一個集合若不是有窮的(例如,整數(shù)集合)就是無窮的(infinite)。無窮集也有大小——這是個有趣的主題,我們將在第7章再繼續(xù)討論。
從一個集合到另一個集合的函數(shù)(function)是一項規(guī)則,該規(guī)則將第一個集合的每個成員與第二個集合的唯一一個成員相關(guān)聯(lián)。若f是從X到Y的函數(shù)且x∈X,則f(x)是Y的成員并且由函數(shù)f將其與x相關(guān)聯(lián),我們稱x是f的自變量(argument),f(x)是自變量為x的函數(shù)f的值(value)。用f:X→Y表示f是一個從集合X到集合Y的函數(shù)。例如,我們可以用b:P→D來表示將八個朋友中的每一個與他或她出生的星期幾相關(guān)聯(lián)的函數(shù),比如,若Charlie出生在星期四,則有b(Charlie)=星期四。
函數(shù)f:X→Y有時也被稱為“從X到Y的映射(mapping)”,或“f將元素x∈X映射到元素f(x)∈Y”。(同樣,現(xiàn)實中的地圖就是將地球表面上的一個點與紙上的一個點相映射。)
最后,我們將例1.1背后的基本原理表述如下。
定理1.2 若有f:X→Y并且X>Y,則存在元素x1,x2∈X,使得x1≠x2且f(x1)=f(x2)。
定理1.2就是著名的鴿籠原理(Pigeonhole principle),因為它以數(shù)學(xué)的形式表述了這個具有普遍意義的思想:當(dāng)鴿子數(shù)大于鴿籠數(shù)且每只鴿子都進入了鴿籠時,某個鴿籠中必有不止一只鴿子。鴿子是集合X的成員,鴿籠是集合Y的成員(見圖1.3)。
我們將在第3章給出鴿籠原理的規(guī)范證明,其中我們會詳細研究證明的基礎(chǔ)技術(shù)。現(xiàn)在,我們來深入探討鴿籠原理的數(shù)學(xué)語言表述。下面是我們可能會問到的一些問題。
1.X和Y是什么?
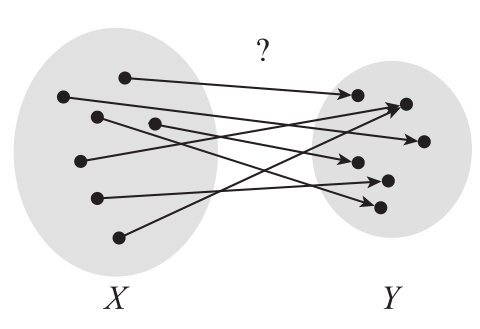
圖1.3 鴿籠原理。若|X|>|Y|并且f是從X到Y的任意函數(shù),那么必然對于X中某兩個不同成員,它們的f值相同
它們都是有窮集。為了清晰起見,我們可以用短語“對于任意有窮集X和Y”作為命題的開始,而只有當(dāng)X和Y是集合時,f是從X到Y的函數(shù)的斷言才有意義。此外,根據(jù)上下文可知,所討論的集合是有窮集,因此我們知道如何比較它們的大小。
2.為什么選擇x1和x2作為集合X中元素的名稱?
原則上,我們可以選擇任意變量名稱,如x和y,但是使用與X相關(guān)的變量名來命名集合X的元素可以表明x1和x2是集合X的成員,而不是集合Y的成員。因此使用x1和x2會使命題更容易理解。
3.短語“使得x1≠x2”真的有必要嗎?沒有它,語句會更簡單,并且有無它似乎說法是同樣的。
是的,短語是必要的,如果沒有它,說法是不一樣的。如果我們不指出x1≠x2,那么x1和x2可以取同一元素。如果不規(guī)定x1和x2必須是不相同的,這個命題雖然不為假,但是沒有任何意義。顯然,當(dāng)x1=x2時,有f(x1)=f(x2)。這就如同地球的質(zhì)量等于距離太陽第三遠的行星的質(zhì)量一樣。另一種鴿籠原理的表述是:存在不同的元素x1,x2∈X,使得f(x1)=f(x2)。
這里還有一點需要強調(diào)。像“存在不同的元素x1,x2∈X,具有……性質(zhì)”的命題并不意味著恰好只有兩個元素具有該性質(zhì),而是說至少有兩個這樣的元素使命題為真,元素可能會更多,但肯定不會更少。
數(shù)學(xué)家們對任何原理總是希望尋找其最泛化的形式,因為這樣可以解釋更多的事情。例如,同樣明顯的命題是,我們不能將15只鴿子放在7個鴿籠里,除非某個鴿籠中至少放有3只鴿子——這種情況是無法從鴿籠原理推得的。下面是鴿籠原理更泛化的版本。
定理1.3 擴展鴿籠原理。對于任意有窮集X和Y以及任意正整數(shù)k,且X>kY,若有f:X→Y,則至少有k+1個不同的成員x1,…,xk+1∈X,使得f(x1)=…=f(xk+1)。
鴿籠原理是擴展鴿籠原理中k=1時的情況。
這里首次使用了序列(sequence)表示法:同一變量名帶有一定范圍的數(shù)字下標(biāo)。在此情況下,xi(1≤i≤k+1)就構(gòu)成了一個長度為k+1的序列。這種表示法非常方便,因為它可以在下標(biāo)中使用像k+1這樣的代數(shù)表達式。類似地,我們可以推斷出序列y1,y2,…的第2i個成員是y2i。
當(dāng)應(yīng)用于特定集合X和Y時,已知X和Y的大小,便可推出擴展鴿籠原理中參數(shù)k的最小值。這有助于使計算更精確。
如果![]() 的商是一個整數(shù)(即q除以p沒有余數(shù)),則稱整數(shù)p整除(divide)整數(shù)q,記為p|q。用
的商是一個整數(shù)(即q除以p沒有余數(shù)),則稱整數(shù)p整除(divide)整數(shù)q,記為p|q。用![]() 表示p不能整除q,例如,
表示p不能整除q,例如,![]() 。對于任意實數(shù)x,我們用
。對于任意實數(shù)x,我們用![]() 表示小于或等于x的最大整數(shù),稱為x的下取整(floor)。例如,
表示小于或等于x的最大整數(shù),稱為x的下取整(floor)。例如, 。同樣還需要上取整(ceiling)的表示方法:
。同樣還需要上取整(ceiling)的表示方法:![]() 表示大于或等于x的最小整數(shù),例如
表示大于或等于x的最小整數(shù),例如![]() 。
。
借助于這些符號,我們從“在已知鴿子和鴿籠數(shù)的情況下,確定占用同一個鴿籠的最多鴿子數(shù)的最小值”的角度重申擴展鴿籠原理。
定理1.4 擴展鴿籠原理(另一個版本)。設(shè)X和Y是任意有窮集,且有f:X→Y。則存在y∈Y,使得f(x)=y,其中x的取值至少為 。
。
證明:設(shè)m=|X|和n=|Y|。如果n|m,那么這是擴展鴿籠原理中 的情況。如果
的情況。如果![]() ,那么這是擴展鴿籠原理中
,那么這是擴展鴿籠原理中 的情況,因為
的情況,因為 是小于
是小于![]() 的最大整數(shù)。■
的最大整數(shù)。■
泛化的鴿籠原理似乎均以奇妙的方式表述了一些顯然的事情。此外,一旦分析出哪些是鴿子哪些是鴿籠,我們就能使用它們?nèi)ソ忉尨罅坎煌默F(xiàn)象。讓我們以數(shù)論(number theory)(對整數(shù)性質(zhì)的研究)中的應(yīng)用來結(jié)束本章。首先是一些基礎(chǔ)知識。
如果p|q,那么稱p為q的因子(factor)或除數(shù)(divisor)。
質(zhì)數(shù)(prime,也稱素數(shù))是一個大于1的整數(shù),它只能被自身和1整除。例如,7是質(zhì)數(shù),因為它只能被7和1整除,但6不是質(zhì)數(shù),因為6=2×3。注意1本身不是質(zhì)數(shù)。
定理1.5 算術(shù)基本定理。一個大于1的整數(shù)有且僅有一種形式表示為不同質(zhì)數(shù)(按遞增順序且具有正整數(shù)次冪)的乘積。
例1.6 我們將在第4章證明這個定理,此處僅給出它的應(yīng)用。將一個數(shù)n質(zhì)分解(prime decomposition)就是將其表示為唯一的質(zhì)數(shù)乘積形式:
其中pi是遞增的質(zhì)數(shù),ei是正整數(shù)。例如,180=22×32×51,并且不存在其他的質(zhì)數(shù)乘積![]() 等于180,其中p1<p2<…<pk,所有的pi都是質(zhì)數(shù),ei都是整數(shù)冪。
等于180,其中p1<p2<…<pk,所有的pi都是質(zhì)數(shù),ei都是整數(shù)冪。
兩個整數(shù)m和n的乘積的質(zhì)分解是由m的質(zhì)分解與n的質(zhì)分解結(jié)合起來的,即m·n的每個質(zhì)因子一定是m或者n的質(zhì)因子。
定理1.7 如果m、n和p都是大于1的整數(shù),p是質(zhì)數(shù),且p m·n,則有p m或者pn。
證明:根據(jù)算術(shù)基本定理(定理1.5),有且僅有唯一的質(zhì)分解如下:
其中pi是質(zhì)數(shù)。那么p必為pi之一,并且每個pi必然出現(xiàn)在m或者n的唯一質(zhì)分解式中。■
在m·n的質(zhì)分解中,質(zhì)數(shù)p的冪是其在m和n的質(zhì)分解中的冪之和(如果質(zhì)分解中沒有出現(xiàn)p,則其冪計算為0)。例如,從乘積18×10=180,可以得到

可以看出,乘積180中2、3和5的冪是它們在兩個因子18和10的分解中的冪之和。
有關(guān)質(zhì)數(shù)的另一個重要事實是有無窮多個質(zhì)數(shù)。
定理1.8 不存在最大質(zhì)數(shù)(即有任意大的質(zhì)數(shù))。
“任意大”意味著對于每一個n>0,都存在一個大于n的質(zhì)數(shù)。
證明:設(shè)k取某個值,則我們可以得到至少k個質(zhì)數(shù),設(shè)p1,…,pk為遞增的前k個質(zhì)數(shù)。(我們可以取k=3,則有p1=1、p2=2、p3=5。)我們將展示如何找到一個大于pk的質(zhì)數(shù)。由于這個過程可能會無限地重復(fù)下去,因此必定會得到無窮多個質(zhì)數(shù)。
例1.9 來看一下比前k個質(zhì)數(shù)乘積大1的數(shù)N:
N=(p1·p2·…·pk)+1
N除以p1,…,pk中的任何一個數(shù),余數(shù)都為1。所以N不存在小于或等于pk的質(zhì)因子。因此,要么N不是質(zhì)數(shù)且有一個大于pk的質(zhì)因子,要么N本身就是質(zhì)數(shù)。■
例如,在k=3的情況下,N=2×3×5+1=31。N本身是質(zhì)數(shù),習(xí)題1.11中要求找到一個N不是質(zhì)數(shù)的例子。
兩個數(shù)的公約數(shù)(common divisor)是能夠整除這兩個數(shù)的數(shù)。例如,21和36具有公約數(shù)1和3,而16和21沒有大于1的公約數(shù)。
在上述定理的基礎(chǔ)上,我們來舉一個鴿籠原理在數(shù)論中應(yīng)用的例子。
例1.10 在2和40之間(包括2和40)選出m個不同的數(shù),其中m≥13。那么至少存在兩個數(shù)有大于1的公約數(shù)。
“在a和b之間(包括a和b)”代表所有≥a且≤b的數(shù),因此該例中包括2和40。
解:首先觀察到,有12個質(zhì)數(shù)小于或等于40:2、3、5、7、11、13、17、19、23、29、31、37。其中任意兩個數(shù)不存在大于1的相同因子(公約數(shù))。定義P為這12個質(zhì)數(shù)的集合。(我們需要指定m≥13,因為m=12時該論斷為假,集合P將是一個反例。)現(xiàn)在考慮具有m個數(shù)(取值范圍為2~40,包括2和40)的集合X。將X的成員看作鴿子,P的成員看作鴿籠。將鴿子放到鴿籠中,定義函數(shù)f:X→P,其中f(x)是整除x的最小質(zhì)數(shù)。例如,f(16)=2、f(17)=17、f(21)=3。根據(jù)鴿籠原理,由于m>12,則對于X的兩個不同成員,必有其f的值相等,因此X中至少有兩個成員有公約數(shù)。■
- 數(shù)字經(jīng)濟:“數(shù)字中國”頂層規(guī)劃與實踐路徑
- 粵港澳大灣區(qū)觀察:帶你看清大灣區(qū)八大產(chǎn)業(yè)發(fā)展前景(《21世紀經(jīng)濟報道》深度觀察)
- 魔鬼數(shù)學(xué):大數(shù)據(jù)時代,數(shù)學(xué)思維的力量
- 數(shù)量經(jīng)濟研究(2018年/第9卷/第2期)
- 穿透數(shù)據(jù):經(jīng)濟數(shù)據(jù)理解要點與分析應(yīng)用(職業(yè)教育經(jīng)濟管理類新形態(tài)系列教材)
- 統(tǒng)計學(xué)
- 算力:數(shù)字經(jīng)濟的新引擎
- 數(shù)量經(jīng)濟研究(2017年/第8卷/第2期)
- 定性數(shù)據(jù)的統(tǒng)計分析
- 數(shù)字化與數(shù)字經(jīng)濟
- 數(shù)學(xué)史講義概要
- 數(shù)量經(jīng)濟研究(2016年/第7卷/第1期)
- 走向數(shù)字經(jīng)濟
- 數(shù)量經(jīng)濟研究(2017年/第8卷/第1期)
- 數(shù)量經(jīng)濟研究(2019年/第10卷/第1期)