- 計算機科學中的離散數學基礎
- (美)哈瑞·劉易斯 雷切爾·扎克斯
- 4032字
- 2025-08-07 15:17:33
第5章 集合
集合(set)是相互可區分的對象的匯集,這些對象被稱為該集合的成員(member)。在第1章我們已經給出了集合的定義,本章將重溫集合的概念。例如,一個集合可以由三個數字2、5和7構成,用花括號來表示。集合僅含有2、5和7,記為{2,5,7}。集合的成員本身也可以是一個集合。例如,集合{{2,5,7}}僅包含一個成員,這個成員就是集合{2,5,7}。前面提到的兩個集合是不相同的,即
{2,5,7}≠{{2,5,7}}
第一個集合有三個成員,第二個集合有一個成員。它們與集合{{2},{5},{7}}又不相同,后者有三個成員,每個成員本身又是一個集合,即只包含一個成員的集合。
當我們說集合的成員是相互可區分(distinct)時,是指集合中沒有重復的對象。例如,如果五名學生參加考試,獲得的分數分別為83、90、90、100和100,那么這五名學生考試分數的集合就是{83,90,100}[1];集合中成員之間的順序無關,即集合{90,100,83}與集合{83,90,100}相等,因為它們具有相同的成員。
下面介紹一些常用的集合,它們有專門的名稱:
?={…,-3,-2,-1,0,1,2,3,…}=整數的集合
?={0,1,2,3,…}=非負整數的集合,也是自然數(natural number)的集合
?=實數(real number)的集合
?=有理數(rational number)的集合
?={}=空集(empty set),即不包含任何元素的集合
一個集合的子集(subset)是由該集合中抽取出來的元素(可以不是全部元素)構成的集合。例如,?是?的子集,?是?的子集,而空集?是任意集合的子集。我們用A?B表示A是B的子集(A也可能等于B)。如果我們要定義A是B的一個子集但不等于B時,記作![]() 。如果
。如果![]() ,則稱A為B的真子集(propersubset)。(有時也用?表示,因為?既像
,則稱A為B的真子集(propersubset)。(有時也用?表示,因為?既像![]() 又像
又像![]() ,會導致意義不清晰,所以近來的數學記法中避免使用。)
,會導致意義不清晰,所以近來的數學記法中避免使用。)
計算機科學家們將集合和數字(整數和實數)定義為基本數據類型(data type)。然而,從基礎數學的觀點來看,如果我們能夠構造集合,就沒有必要將數字視為基本數據類型,因為數字可以用集合來定義,計算機科學家們稱之為編碼技巧。一旦有更復雜的歸納定義和證明技術,我們便可以探討這些編碼了(見習題8.7)。
如果A是B的子集,則B稱為A的超集(superset)。如果A是B的真子集,則B稱為A的真超集(proper superset)。
前面說過,集合的成員也可以是集合。一個很重要的例子就是集合A的冪集(power set),我們用P(A)來表示,它是A的所有子集的集合。例如,當A={3,17}時,有
P(A)={?,{3},{17},{3,17}}
我們使用符號∈表示集合與成員的關系。例如,a∈S表示a是集合S的成員,并且下述命題
2∈{2,5,7}為真
而3∈{2,5,7}為假
類似地,有?∈P(?),因為所有整數的集合是有理數集合的子集。符號?表示給定的元素不在給定的集合中,例如,3?{2,5,7}。空集是唯一沒有元素的集合,即不存在x,使得x∈?。
下列情況不能被混淆。
? 1和{1}:1是一個數字,而{1}是一個只包含一個對象的集合,即數字1。
? 0和?:0是一個數字,而?是一個特別的集合,即空集。{?}是不同于前兩者的第三種事物,即只包含一個元素的集合,其元素是空集?。
? ∈和?:1∈{1,2},因為1是{1,2}中的元素之一。但是,1?{1,2}不為真,1不是集合,因此就不能是子集。(計算機科學家們會說1?{1,2}是類型匹配錯誤,因為?兩邊的實體必須是集合。)此外,有{1}?{1,2},并且![]() ,但是{1}?{1,2},因為{1,2}的元素不是集合而是數字[2]。
,但是{1}?{1,2},因為{1,2}的元素不是集合而是數字[2]。
一個集合可以是有限的或有窮的(finite)也可以是無限的或無窮的(infinite)。如果它的成員數等于某個非負整數,那么它是有限的。例如,?有0個成員,所以它是有限的;如果A={3,17},那么P(A)={?,{3},{17},{3,17}}有4個成員,因此它也是有限的。計算P(A)時,要記住它是一個集合的集合,而不是數字的集合,所以我們要計算它所包含的集合數,而不是這些集合中的數字數。
我們用|S|表示集合S的大小,稱之為S的基數(cardinality)。因此,有|?|=0。如果A={3,17},那么|A|=2,|P(A)|=|{?,{3},{17},{3,17}}|=4。
整數集合是無限的,所有偶數的集合{…,-4,-2,0,2,4,…}也是無限的。可以充分地說明,任意集合不是有限的就是無限的。對于兩個無限集合來說,可以是相同大小的,也可以是不同大小的。例如,整數集合和偶數集合,它們是不相同的無限集合,卻具有相同的大小。也存在大小不同的無限集合,例如,整數集合和實數集合。我們將在第6章再回到無限集合大小問題的討論。
|{?}|是什么?像P(A)一樣,這是一個由集合構成的集合,所以我們不在意內部集合的大小,即使它們是無限的。所以|{?}|=1,因為{?}只包含單個對象?,而不考慮?是否是一個無窮集。
有時我們需要更規范的方式表示“整數”或“有理數”。不像前面那樣,以列出成員樣例的方式來表示“偶數”的集合,我們使用下面的表示法[3]:
{n∈?:n是偶數}
或者等價地表示為
{n∈?:n=2m,m∈?}
又或者表示為
{2m:m∈?}
一般來說,A中滿足謂詞P的元素的集合表示為
{x∈A:P(x)}
對P(x)的另一種解釋是:x具有性質P。
用現有的集合構建新的集合有多種方法。當有兩個集合A和B時,我們可以得到它們的并集(union),即包含在A或B中的元素構成的集合,以及它們的交集(intersection),即既在A中又在B中的元素構成的集合。這些概念通常使用文氏圖(Venn diagram)來說明,如圖5.1~圖5.3所示,圖中展示了兩個有重疊的集合A和B,以及它們的并集和交集。
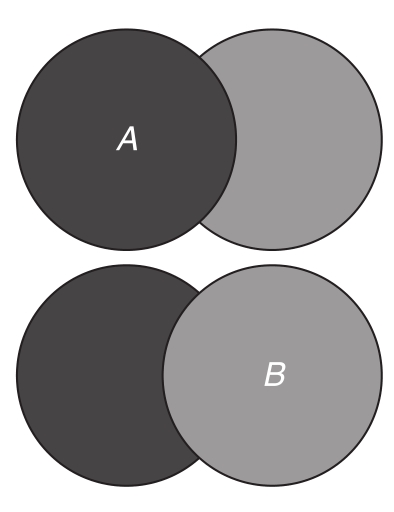
圖5.1 集合A和B重疊
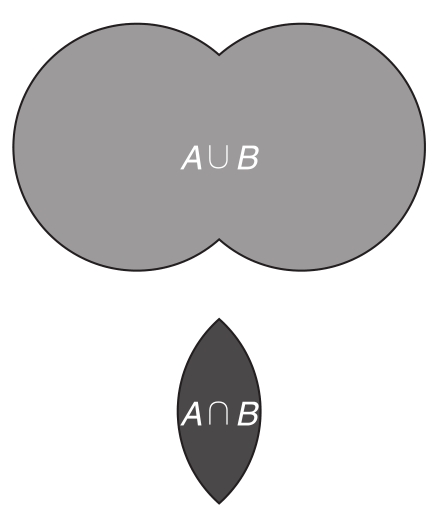
圖5.2 圖5.1中集合A和B的并集和交集
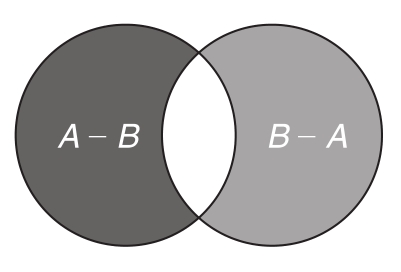
圖5.3 A和B之間的差表示為A-B和B-A
A和B的并集記為
A∪B={x:x∈A或x∈B}
A和B的交集記為
A∩B={x:x∈A且x∈B}
像數字的加法和乘法一樣,集合的“并”和“交”也具有可結合(associative)性,即
(A∪B)∪C=A∪(B∪C)
對于任意的集合A、B和C,同樣地,有
(A∩B)∩C=A∩(B∩C)
我們將在第9章再回到這個主題,此刻只要注意到“或”和“且”在自然語言中是可結合的就足夠了。例如,“你是17歲以上的女性,并且還是美國人”與“你是17歲以上,并且是女性美國人”是完全一樣的。構造“17歲以上的人”、“女性”和“美國人”三個集合,通過“先對前兩個集合取交集,然后再與第三個集合取交集”和“先對后兩個集合取交集,然后再與第一個集合取交集”,兩種方式都可以獲得三個集合的交集。類似地,集合的并和交的運算都是可交換的(commutative),即對于任意的集合A和B,有A∪B=B∪A和A∩B=B∩A成立。
我們還可以求集合的補集(complement),表示為![]() 。全集U(universe)可以是任何可能事物x的集合,x沒有確切的定義,它的意義是由上下文決定的,但是意義并不模糊。如果B={x∈U:P(x)},那么我們可以得到
。全集U(universe)可以是任何可能事物x的集合,x沒有確切的定義,它的意義是由上下文決定的,但是意義并不模糊。如果B={x∈U:P(x)},那么我們可以得到![]() 。例如,如果B={星期六,星期天},那么假設“星期三”
。例如,如果B={星期六,星期天},那么假設“星期三”![]() 是沒有問題的,但“一月”
是沒有問題的,但“一月”![]() 可以嗎?這完全取決于U是“星期幾的集合”,還是“自然語言中所有單詞的集合”,或者其他的集合含義。
可以嗎?這完全取決于U是“星期幾的集合”,還是“自然語言中所有單詞的集合”,或者其他的集合含義。
當我們有了補集的概念,便可以做A和B的差(difference),即在A中而不在B中的元素,表示為:
圖5.3展示了圖5.1中的集合A和B的A-B和B-A。這兩個表達式意義完全不同,在示例中,兩者都不為空。一般來說,有
A∪B=(A-B)∪(B-A)∪(A∩B)
也就是說,A∪B是兩個集合之差(兩邊的部分)的并集,再與集合交集(中間“缺失部分”)的并。
集合差A-B有時也表示為A\B。
集合的并和交運算滿足分配律,類似于算術運算中加法和乘法的分配律,即a·(b+c)=a·b+a·c。這里有一個重要的區別:集合的并和交運算的分配律是對稱的。
定理5.1 分配律。
A∩(B∪C)=(A∩B)∪(A∩C)
A∪(B∩C)=(A∪B)∩(A∪C)
我們只證明第一個等式,第二個等式留作習題5.2。
證明:考慮任意元素x,首先假設x∈A∩(B∪C)。
根據∩和∪的定義,可以得到:
(a)x是集合A的成員。
(b)(b1)x是集合B的成員。
(b2)x是集合C的成員。
當(b1)為真時,x是A和B的成員;當(b2)為真時,x是A和C的成員,即x∈(A∩B)∪(A∩C)。
現在假設x∈(A∩B)∪(A∩C)。我們可以按照上述相同的推理過程反向推理。無論x∈(A∩B)還是x∈(A∩C),x都是A的成員,并且也必須是B或C的成員,即x∈A∩(B∪C)。■
上述論證過程在集合及其∪、∩運算的規律與命題及其連接詞“或”和“且”的推理之間交替進行。形式化“復合命題的真值取決于組成該命題的原子命題的真值”的推理過程是命題演算的主要內容,也是第9章的主題。事實上,集合運算具有與命題邏輯中同樣的結合律、交換律和分配律(見第9章)。
并和交運算的符號∪和∩如同擴展和與擴展積的符號Σ和Π一樣。例如,?是所有具有一個元素的集合{n}的并集,即對于任意的n∈?,?可以表示為
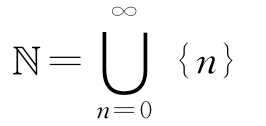
集合S是全集U(除了不在S中的單個元素之外的所有事物)的所有子集的交集,則S表示為
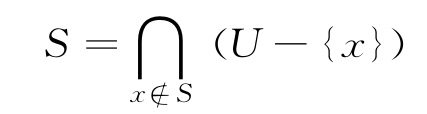
有序對(ordered pair)〈x,y〉是一種數學結構,它將元素(component)x、y組合成一個順序結構。也就是說,〈x,y〉不同于〈y,x〉,除非x與y相同。總之,只有在x=z和y=w的情況下,才有〈x,y〉=〈z,w〉。
〈x,y〉也不同于{x,y}({x,y}與{y,x}是相同的)。我們將把有序對〈x,y〉視為不同于集合的另一種基本數據類型。
事實上,可以用集合來定義有序對,如同可以用集合來定義數字一樣。數學的純粹主義者和基本教義派有時會將有序對〈x,y〉定義為{x,{x,y}},他們認為,基本概念盡可能地少是很重要的。根據這種定義,有序對具有如下基本性質,即兩個有序對是相等的當且僅當它們中的第一、第二個元素分別對應相等(見習題5.11)。
有序對的概念可以擴展到有序三元組。我們用〈x,y,z〉表示由三個元素x、y和z構成的有序三元組。一般地,我們統稱為有序n元組(ordered n-tuple),其中n是非負整數,表示有n個元素的序列。兩個有序n元組是相等的,當且僅當對于每個i,它們的第i個元素都是相等的,1≤i≤n。
由第一元素來自集合A和第二元素來自集合B的所有有序對構成的集合稱為A和B的笛卡兒積(Cartesian product)或叉積(cross product),表示為A×B。例如,如果A={1,2,3},B={-1,-2},則
A×B={〈1,-1〉,〈1,-2〉,〈2,-1〉,〈2,-2〉,〈3,-1〉,〈3,-2〉}
很明顯,A×B通常不同于B×A。如果A和B都是有窮集,那么有|A×B|=|A|·|B|。在上面的例子中,有|A|=3、|B|=2,且|A×B|=6。我們也可以構造無窮集的笛卡兒積,如?×?是所有整數的有序對集合,其中第一個元素是非負的整數,有
{1,2,3}×{-1,-2}??×?