- 計算機科學中的離散數學基礎
- (美)哈瑞·劉易斯 雷切爾·扎克斯
- 640字
- 2025-08-07 15:17:33
習題
4.1 設a1=0、a2=6、a3=9。對于n>3,an=an-1+an-3。證明對于所有n,an可被3整除。
4.2 證明對于所有的n≥8,存在整數a和b,使得n=3a+5b,即n是多個3與多個5的和。
4.3 證明對于任意的n>1,可以使用由三個正方形組成的L形磚片(見圖4.13)平鋪一個2n×2n正方形,只留角上有一個空白的正方形(見圖4.14)。其中,L形磚片可以以任何方向旋轉和使用。

圖4.13 L形磚片
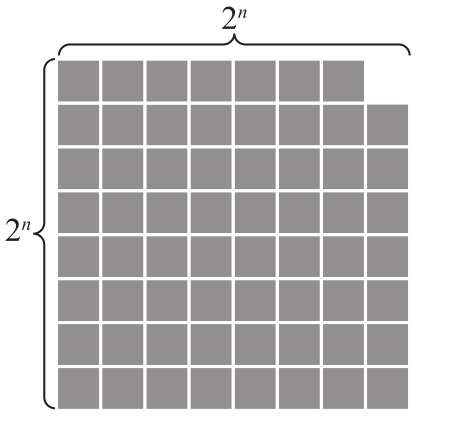
圖4.14 L形磚片覆蓋了每個小方塊,除了角上的一塊(n=3的情況)
4.4 假設已知實數x,使得 是整數。應用強歸納法證明:對于任意整數
是整數。應用強歸納法證明:對于任意整數![]() ,都有
,都有 是整數。
是整數。
提示:將乘積 展開找到一個有助于歸納的等式。
展開找到一個有助于歸納的等式。
4.5 設S是一個數列a1,a2,a3,…,其中a1=1、a2=2、a3=3,并且對于任意的n≥4,有an=an-1+an-2+an-3。應用強歸納法證明:對于任意的正整數n,有an<2n。
4.6 證明:能夠用強歸納法證明的任意命題都可以用基本歸納法證明。
4.7 證明:質分解式是唯一的,即如果有
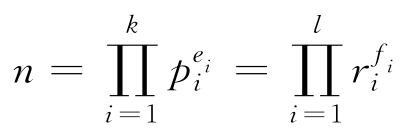
其中pi、ri都是遞增的質數,且所有指數ei、fi都是正整數,那么存在k=l,對于每個i,有pi=ri、ei=fi。
4.8(a)證明:數學歸納法蘊含良序原理。提示:對非負整數的非空集合的大小進行歸納,假設“如果一個集合非空,那么就能找到它的一個成員”。
(b)證明:良序原理蘊含數學歸納法。提示:假設P(n0)為真,并且對于每一個n,有“如果P(n)為真,則P(n+1)為真”。由于某些原因,P(n)不是對于所有的n≥n0都為真。關于非負整數集合中P為假的原因。
4.9 應用算術基本定理證明中給出的方法,找到100的質分解式。展示每個階段的S、p和q的值。
4.10 假設你能買到的郵票只有2美分和3美分兩種面值。證明只要n≥2,n美分的郵費最多使用![]() 張郵票。
張郵票。