- 計(jì)算機(jī)科學(xué)中的離散數(shù)學(xué)基礎(chǔ)
- (美)哈瑞·劉易斯 雷切爾·扎克斯
- 4687字
- 2025-08-07 15:17:32
第4章 強(qiáng)歸納法
數(shù)學(xué)歸納法是一種功能強(qiáng)大且應(yīng)用廣泛的證明方法,但在某些情況下它似乎還不夠強(qiáng)大。這里有一個(gè)簡(jiǎn)單的例子,它融合了上一章的歸納范例,但又不完全相同。為了解答這個(gè)問(wèn)題,我們需要一個(gè)更強(qiáng)版本的歸納法。
例4.1 有一款簡(jiǎn)單的游戲,需要兩名玩家和一堆硬幣。我們將兩個(gè)玩家分別稱作Ali和Brad。從Ali開(kāi)始,然后兩名玩家輪流拿硬幣。游戲規(guī)則有兩條:
1.玩家在每輪需要拿起一至兩枚硬幣。
2.拿到最后一枚硬幣的玩家失敗。
如果每名玩家都足夠聰明,那么誰(shuí)會(huì)贏呢?
答案取決于開(kāi)始時(shí)有多少枚硬幣。設(shè)硬幣數(shù)量為n,通過(guò)嘗試較小的n值,看看我們能否找到解決問(wèn)題的模型。
? 當(dāng)n=1時(shí),Ali失敗,因?yàn)樗仨毮闷鹬辽僖幻队矌牛挥幸幻队矌拧K运仨毮闷疬@“最后一枚”硬幣。對(duì)于Ali來(lái)說(shuō),n=1是使其必輸?shù)那闆r(見(jiàn)圖4.1)。
? 如果n=2,情況又會(huì)如何呢?Ali也可能失敗,在她愚蠢地拾起兩枚硬幣時(shí)發(fā)生。但在分析問(wèn)題之前,我們已經(jīng)假定Ali和Brad都是足夠聰明的。如果Ali拾起1枚硬幣,就會(huì)留下1枚硬幣給Brad,從而迫使他陷入必輸?shù)木车亍#ㄗ⒁膺@里有一個(gè)重要的概念:如果n是使Ali輸?shù)粲螒虻那闆r,那么它也可能是使Brad輸?shù)粲螒虻那闆r,即只剩一枚硬幣留給Brad。)因此,以2枚硬幣開(kāi)始的游戲,對(duì)Ali來(lái)說(shuō)是獲勝的情況,因?yàn)樗梢云仁笲rad陷入必輸?shù)木车兀ㄒ?jiàn)圖4.2)。
? 如果開(kāi)始時(shí)有3枚硬幣,那么Ali可以拾起2枚硬幣,這再次使Brad陷入必輸?shù)木车亍R虼耍?枚硬幣開(kāi)始的游戲,會(huì)得到Ali獲勝的情況(見(jiàn)圖4.3)。

圖4.1 當(dāng)n=1時(shí),Ali失敗
圖4.2 當(dāng)n=2時(shí),Ali獲勝
圖4.3 當(dāng)n=3時(shí),Ali獲勝
? 如果開(kāi)始時(shí)有4枚硬幣,那么Ali有兩種選擇,但是無(wú)論哪種選擇,她都無(wú)法獲勝。她可以拿起一枚硬幣,留下3枚;也可以拿起兩枚硬幣,剩下兩枚。但是接下來(lái),比賽就交給了Brad,此時(shí)這堆硬幣有3枚或者兩枚,都是Brad獲勝的情況(見(jiàn)圖4.4和圖4.5)。
圖4.4 當(dāng)n=4時(shí),如果Ali拾起1枚硬幣,則失敗
圖4.5 當(dāng)n=4時(shí),如果Ali拾起2枚硬幣,則失敗
? 再試一種情況,即在游戲開(kāi)始時(shí)n=5。Ali可以拿起一枚硬幣,留給Brad4枚硬幣。對(duì)Brad來(lái)說(shuō),這是一個(gè)必輸?shù)木置妫拖馎li面對(duì)4枚硬幣的情況一樣。因此,5枚硬幣是Ali獲勝的情況(圖4.6)。
對(duì)于一個(gè)玩家來(lái)說(shuō),面對(duì)n枚硬幣是贏還是輸似乎取決于n被3除時(shí)的余數(shù)是0、1還是2:
1.如果n除以3的余數(shù)為0或2,那么面對(duì)n枚硬幣就是贏的局面。
2.如果n除以3的余數(shù)為1,那么面對(duì)n枚硬幣就是必輸?shù)木车亍?/p>
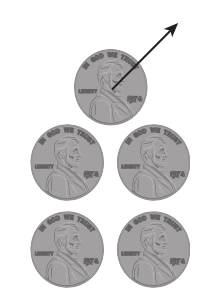
圖4.6 當(dāng)n=5時(shí),Ali獲勝
情況1和情況2是相互依存的。如果余數(shù)為1,那么拿起1或2枚硬幣將分別創(chuàng)建余數(shù)為0或2的硬幣堆,這是使另一方獲勝的選擇。也就是說(shuō),如果存在某個(gè)整數(shù)n,使得n=3k+1,那么n-1可以被3整除,并且有
n-2=3(k-1)+2
即除以3余數(shù)為2。如果余數(shù)是0或2,那么拿起2枚或1枚硬幣,將創(chuàng)建一個(gè)余數(shù)為1的硬幣堆,這是使另一方輸?shù)粲螒虻那闆r。
因此,我們做出以下猜想。
猜想:對(duì)于任意的n≥1,開(kāi)始時(shí)有n枚硬幣,對(duì)于Ali是輸?shù)粲螒虻那闆r,當(dāng)且僅當(dāng)存在某個(gè)整數(shù)k,使得n=3k+1。
由于情況1和情況2的相互關(guān)聯(lián)性,這一猜想看上去很適合用數(shù)學(xué)歸納法來(lái)描述,除了一個(gè)小小的“瑕疵”外,即n枚硬幣的論證不僅取決于n-1枚硬幣,還取決于n-2枚硬幣的歸納假設(shè)。下面先給出猜想的證明,然后給出公式化的強(qiáng)歸納法。
解:我們將用歸納法對(duì)n進(jìn)行歸納來(lái)證明前面的猜想。
歸納基礎(chǔ)。對(duì)于n0=1和n1=2的情況,猜想為真,因?yàn)閷?duì)于Ali來(lái)說(shuō),前者(n0=3·0+1)是輸?shù)粲螒虻那闆r,而后者(n1=3·0+2)是獲勝的情況。正如前面所論述的那樣。
歸納假設(shè)。假設(shè)對(duì)于任意的n≥2和任意的m,使得1≤m≤n,m枚硬幣是使Ali輸?shù)粲螒虻那闆r,當(dāng)且僅當(dāng)m除以3的余數(shù)為1。
歸納步驟。假設(shè)Ali面對(duì)的是n+1枚硬幣(n≥2),Ali可以拿起一枚或者兩枚硬幣,留下n枚或者n-1枚硬幣給Brad。由于n≥2,那么n和n-1是大于或等于1并且小于或等于n的數(shù)。
如果n+1除以3的余數(shù)為1,則n和n-1的余數(shù)分別為0和2。又由于n和n-1都是小于或等于n的數(shù),根據(jù)歸納假設(shè),這兩個(gè)數(shù)都是使Brad獲勝的情況。因此,n+1對(duì)Ali來(lái)說(shuō)是輸?shù)粲螒虻那闆r。
如果n+1除以3的余數(shù)為0即n+1=3k,那么Ali可以拿起兩枚硬幣,留下n-1=3·(k-1)+1枚硬幣給Brad;又由于n-1<n,根據(jù)歸納假設(shè),n-1是使Brad輸?shù)粲螒虻那闆r。
類似地,如果n+1除以3的余數(shù)為2,Ali可以拿起一枚硬幣,留下3的倍數(shù)加1枚硬幣給Brad,使Brad陷入必輸?shù)木车亍!?/p>
設(shè)謂詞P(n)表示:
以n枚硬幣開(kāi)始且使Ali處于輸?shù)粲螒虻那闆r,當(dāng)且僅當(dāng)n是3的倍數(shù)加1。
這個(gè)論斷涉及前一章中與歸納法無(wú)關(guān)的兩個(gè)特別的特征。首先是已經(jīng)提及的一點(diǎn):為了證明P(n+1),對(duì)于m≤n的多個(gè)值,歸納假設(shè)不僅要包括P(n)為真,還要包括P(m)為真。(在前面的具體論證中,包括了m=n和m=n-1的情況。)這里有一個(gè)有意思的比喻:爬梯子。要爬某一級(jí)臺(tái)階,不僅要爬過(guò)緊挨著這級(jí)臺(tái)階下面的一級(jí)臺(tái)階,而且要爬過(guò)這級(jí)臺(tái)階以下的所有臺(tái)階(圖4.7)。當(dāng)我們爬過(guò)下面的所有臺(tái)階到達(dá)某個(gè)高度時(shí),使用爬過(guò)的任意一級(jí)臺(tái)階作為到更高臺(tái)階的基礎(chǔ)是合理的。

圖4.7 強(qiáng)歸納法:為了登上梯子的更高一級(jí)臺(tái)階,需要爬過(guò)其下所有的臺(tái)階
另外一個(gè)重要的細(xì)節(jié)是,我們需要多個(gè)歸納基礎(chǔ),即在這個(gè)論斷中,歸納基礎(chǔ)包括n=1和n=2兩種情況。這一點(diǎn)很關(guān)鍵,但容易被忽視。在歸納步驟中,我們選取了數(shù)字n+1并從中減去1或2,然后論證“對(duì)P(n)和P(n-1)的真值進(jìn)行歸納”的假設(shè)是安全的。為了做到這一點(diǎn),我們注明n和n-1都是小于或等于n的(顯而易見(jiàn)),并且都大于或等于1。為了使(n+1-2)≥1,我們需要在歸納開(kāi)始時(shí)假設(shè)n≥2,即在歸納基礎(chǔ)論證時(shí),要分別考慮n=1和n=2的情況。
將上述所有考慮放在一起,我們提出強(qiáng)數(shù)學(xué)歸納法(strong principle of mathematical induction):
證明謂詞P(n)對(duì)于大于或等于某個(gè)特定數(shù)n0的任意n都成立。
歸納基礎(chǔ)。證明P(m)成立,對(duì)于任意的m,滿足n0≤m≤n1,其中n1≥n0。也就是說(shuō),n0是最底層臺(tái)階,我們要分別論證對(duì)于n0和n1之間(包括n0和n1)的每個(gè)m有P(m)成立。在硬幣游戲中,有n0=1和n1=2。
歸納假設(shè)。設(shè)對(duì)于任意的n≥n1,P(m)成立,其中n0≤m≤n。
歸納步驟。設(shè)歸納假設(shè)成立,證明P(n+1)成立。
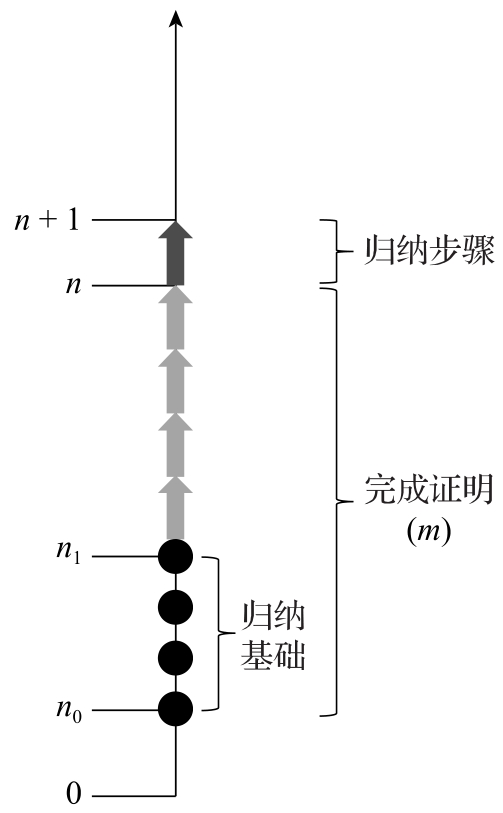
圖4.8 強(qiáng)歸納法框架。歸納基礎(chǔ)為黑色部分,歸納假設(shè)(淺灰色或黑色部分)是“對(duì)所有的m,P(m)均為真”。歸納步驟(灰色部分)證明P(n+1)為真。如果論證中忽略了n≥n1,那么我們的結(jié)論就是P(n)對(duì)所有的n≥n0都成立
強(qiáng)歸納法如圖4.8所示,展示了n為0,1,…的情況。對(duì)于m<n0的情況,P(m)可以不為真。因?yàn)?span id="dddsxd7" class="kt">歸納基礎(chǔ)是n0,…,n1,所以對(duì)于該范圍內(nèi)的每個(gè)m,必須給出相對(duì)應(yīng)的“P(m)為真”的論證。進(jìn)入歸納步驟階段之前,要完成“對(duì)于n0到n之間(包括n0和n)的所有m,有P(m)成立”的證明,m=n1是淺灰色值部分的歸納第一步,淺灰色范圍內(nèi)的所有值也都是歸納基礎(chǔ)。歸納步驟(灰色部分)在已知P(m)對(duì)于n0和n之間的所有淺灰色值均為真的基礎(chǔ)上證明P(n+1)成立。
下面的例子將展示如何使用強(qiáng)歸納法來(lái)證明數(shù)列的性質(zhì)。
例4.2 考慮數(shù)列a1=3和a2=5,對(duì)于所有的n>2,有an=3an-1-2an-2。應(yīng)用強(qiáng)歸納法證明:對(duì)于所有的整數(shù)n≥1,有an=2n+1。
解:設(shè)謂詞P(n)定義為an=2n+1。我們的目標(biāo)是證明對(duì)于任意的n≥1,P(n)成立。歸納基礎(chǔ)。
P(1):a1=21+1=3
P(2):a2=22+1=4+1=5
歸納假設(shè)。對(duì)于某個(gè)n≥2,假設(shè)對(duì)于所有的m,1≤m≤n,有P(m)成立,即am=2m+1。
歸納步驟。證明P(n+1),即an+1=2n+1+1成立。
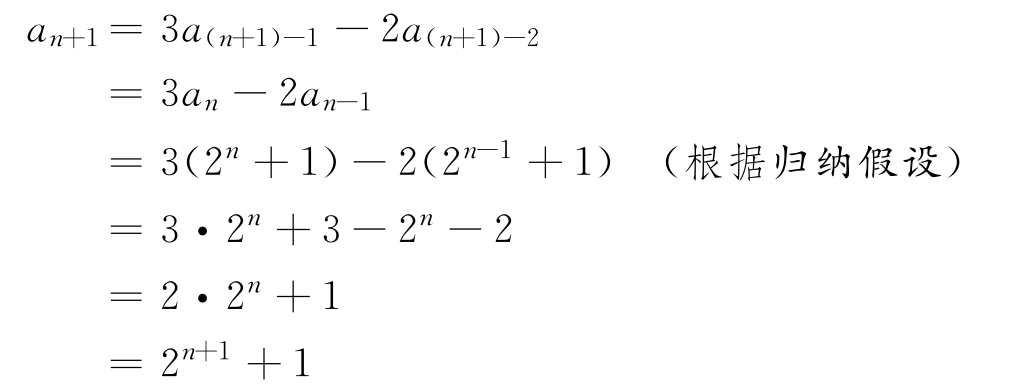
■
下面舉一個(gè)有關(guān)游戲策略的例子。在這個(gè)例子中,歸納不僅關(guān)系到歸納變量的前一個(gè)或兩個(gè)值,還關(guān)系到所有更小的值。我們?cè)俅畏Q玩家為Ali和Brad。
游戲中有一個(gè)巧克力棒,它是由n×p個(gè)“塊”構(gòu)成的網(wǎng)格狀矩形(見(jiàn)圖4.9)。我們使用術(shù)語(yǔ)“塊”來(lái)表示單個(gè)1×1的網(wǎng)格方塊。我們可以沿著巧克力棒長(zhǎng)或?qū)挼娜魏畏较虻慕涌p折斷,將其分成兩個(gè)較小的矩形。
從Ali開(kāi)始。她可以水平或垂直地折斷巧克力棒,從而得到兩個(gè)分離的矩形。(玩家可以將巧克力棒旋轉(zhuǎn)90°,所以“水平”和“垂直”只有在我們的插圖中有意義。)Ali折斷巧克力棒后,吃掉其中一個(gè)矩形,將另一個(gè)矩形遞給Brad。Brad同樣照做,把其中一個(gè)矩形遞給Ali。Ali和Brad就這樣一直做下去,直到某個(gè)人遞給對(duì)方的矩形只有一塊,接受的一方不能再做折斷了,這個(gè)收到1×1矩形的玩家就失敗了。
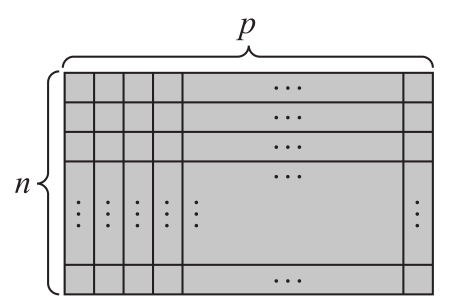
圖4.9 一個(gè)n×p大的巧克力棒
玩家獲勝的最佳策略是什么呢?
讓我們從玩家Ali的角度來(lái)看這個(gè)游戲,并用游戲結(jié)果來(lái)回溯過(guò)程。
Ali的目的是遞給Brad一個(gè)1×1的矩形。如果開(kāi)始的情況就是一個(gè)1×1的矩形(n=p=1),那么她將失敗。如果開(kāi)始的情況是一個(gè)1×p的矩形(任意的p>1),那么她可以折斷p-1塊,把剩下的一塊遞給Brad,Ali獲勝。因此,1×1矩形對(duì)于任何持有它的人來(lái)說(shuō)都是一個(gè)輸?shù)粲螒虻那闆r,但是1×p(或者p×1)的矩形卻是一個(gè)獲勝的情況,其中p>1(見(jiàn)圖4.10)。
如果開(kāi)始的情況是一個(gè)2×2矩形,那么,Ali可以用兩種方式折斷它。但無(wú)論選擇哪種方式,她都會(huì)遞給Brad一個(gè)2×1的矩形(或1×2的矩形,它們是等同的)。此時(shí),Brad具有一個(gè)獲勝的對(duì)策,即Brad可以采用與Ali面對(duì)一個(gè)1×p的矩形時(shí)同樣的對(duì)策。因此,如果開(kāi)始的情況是一個(gè)2×2的矩形,Ali就無(wú)法獲勝(見(jiàn)圖4.11),那么2×2矩形對(duì)任何人來(lái)說(shuō)都是一個(gè)輸?shù)粲螒虻那闆r。
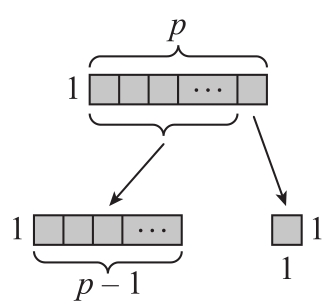
圖4.10 只要p>1,那么1×p或p×1的矩形就是使玩家獲勝的情況,因?yàn)槌钟姓呖梢哉蹟嘁粋€(gè)塊遞給對(duì)方
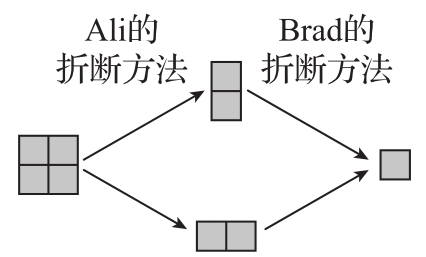
圖4.11 如果Ali面對(duì)的是一個(gè)2×2的矩形,那么她會(huì)失敗
如果開(kāi)始的情況是一個(gè)3×3矩形會(huì)怎樣呢?Ali有多個(gè)選擇:要么給Brad一個(gè)2×3或3×2的矩形(這兩個(gè)效果是一樣的),要么給Brad一個(gè)1×3或3×1的矩形(這兩個(gè)效果也是一樣的)。無(wú)論Ali以哪種方式折斷3×3的巧克力棒,Brad都可以找到一種方法返給Ali一個(gè)更小的矩形(見(jiàn)圖4.12),并且我們知道,如果Ali收到的是1×1或2×2的矩形,那么她都必輸無(wú)疑。
因此,我們推測(cè):如果先手玩家開(kāi)始的情況不是正方形,那么他就有獲勝的對(duì)策;而后手玩家只有在先手玩家開(kāi)始的情況是正方形時(shí),才有獲勝的對(duì)策。
例4.3 從一個(gè)長(zhǎng)寬不相等的n×p矩形(在不失一般性的情況下,設(shè)p>n)開(kāi)始的玩家具有獲勝的對(duì)策:折斷n×(p-n)塊,然后遞給對(duì)手一個(gè)n×n矩形。從一個(gè)n×n矩形開(kāi)始的玩家(對(duì)手使用了上述對(duì)策)將無(wú)法獲勝。
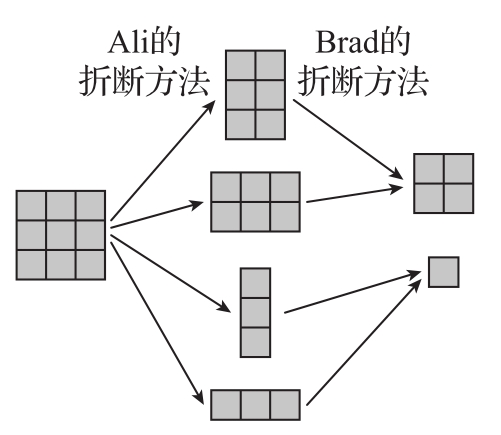
圖4.12 如果Ali面對(duì)的是一個(gè)3×3的矩形,那么她也會(huì)失敗
解:設(shè)矩形的尺寸為n×p,其中p≥n。對(duì)較小維度的n(p等于n除外)進(jìn)行歸納證明。像往常一樣,從Ali開(kāi)始。
歸納基礎(chǔ)。n0=1。如果p=1,那么Ali拿到的是一個(gè)1×1矩形,Ali失敗。如果p>1,那么Ali可以折斷p-1塊[1×(p-1)矩形],并將單獨(dú)一塊遞給Brad。則Brad失敗,Ali獲勝。
歸納假設(shè)。對(duì)于某個(gè)n≥1,假設(shè)對(duì)于所有的m≤n,當(dāng)p>m時(shí),如果玩家的開(kāi)始情況是一個(gè)m×p矩形,則具有獲勝的對(duì)策,即折斷一個(gè)m×(p-m)矩形,并將m×m矩形遞給對(duì)手。如果玩家的開(kāi)始情況是一個(gè)m×m矩形(對(duì)手使用了上述策略),則無(wú)法獲勝。
歸納步驟。假設(shè)Ali的開(kāi)始情況是一個(gè)(n+1)×p矩形,其中p≥n+1≥2。如果p=n+1,則Ali失敗:無(wú)論她如何折斷巧克力棒,都只能遞給Brad一個(gè)(n+1)×m矩形,其中m<n+1。也就是說(shuō),m≤n,但根據(jù)歸納假設(shè),Brad開(kāi)始的情況是兩個(gè)維度不相同且較小的維度小于或等于n的矩形,他有一個(gè)獲勝的對(duì)策。此外,如果p>n+1,那么Ali可以折掉一個(gè)(n+1)×(p-(n+1))矩形,并交給Brad一個(gè)(n+1)×(n+1)矩形,這對(duì)Brad來(lái)說(shuō)是無(wú)法獲勝的情況,與Ali所遇到的情況(p=n+1)完全相同。■
注意在這個(gè)證明中使用強(qiáng)歸納法最重要的部分是:當(dāng)玩家有一個(gè)n×p的矩形,其中p≥n,那么該玩家可以向?qū)κ址祷匾粋€(gè)m維度的矩形(任意的m小于或等于n)。
在前面的示例中,證明P(n)為真,我們的歸納基礎(chǔ)是從n0=0或者n0=1開(kāi)始的。有時(shí),有些謂詞對(duì)于有限數(shù)量的某些n值不為真,那么我們就證明它對(duì)于“足夠大”的值是真的。也就是說(shuō),存在某些n0,使得當(dāng)n<n0時(shí),P(n)可能為假,但對(duì)于任意的n≥n0都為真。在這些情況下,我們把n0作為歸納基礎(chǔ)的開(kāi)始值(要特別當(dāng)心:我們的歸納步驟不依賴于任何使P(n)為假的較小的n值)。
例4.4 一套量杯包括量度為4杯、9杯、11杯和14杯的量杯各一個(gè)。證明這套量杯可用于測(cè)量大于或等于11杯的任何杯數(shù)。
解:要證明的命題泛化形式為P(n)對(duì)于任意的n≥n0=11都成立。
歸納基礎(chǔ)。從11杯開(kāi)始列舉前幾杯的情況。(重要的是,我們需要忽略任何小于11杯的情況,因?yàn)闊o(wú)法用給定的杯子測(cè)量10杯)。因?yàn)橛幸粋€(gè)11杯的量杯,所以我們使用一次就可以測(cè)量出11杯。我們可以三次使用4杯測(cè)量出12杯。對(duì)于13,我們可以使用4杯和9杯的組合。對(duì)于14杯,我們可以使用14杯。因此,如果我們假設(shè)謂詞P(n)表示“可以使用套杯的任意組合測(cè)量出n杯來(lái)”,那么我們已經(jīng)確定了P(11)、P(12)、P(13)和P(14)都為真的四個(gè)歸納基礎(chǔ)。
歸納假設(shè)。對(duì)于任意的n≥n1=14,有P(m)成立,其中n0≤m≤n。
歸納步驟。在假設(shè)P(m)對(duì)n0等于11到n之間(包括n)的所有m均為真的前提下證明P(n+1):由于n+1≥15,我們可以應(yīng)用歸納假設(shè)測(cè)量(n+1)-4杯,因?yàn)椋?i>n+1)-4大于或等于11,這是已經(jīng)證明的情況。我們可以用測(cè)量(n+1)-4杯再加上一個(gè)4杯來(lái)測(cè)量(n+1)杯。■
盡管我們給出的強(qiáng)歸納法好像是全新的、比基本數(shù)學(xué)歸納法更具通用性的方法,但實(shí)際上并非如此。事實(shí)上,能用強(qiáng)歸納法證明的任何命題,也都可以用基本歸納法來(lái)證明,或許不夠巧妙(見(jiàn)習(xí)題4.6)。
由于強(qiáng)歸納法不是新的數(shù)學(xué)原理,只是更便利了,所以當(dāng)我們說(shuō)到歸納法時(shí),不會(huì)嚴(yán)格地區(qū)分使用的是基本歸納法還是強(qiáng)歸納法。
數(shù)學(xué)歸納法還有另外一種看起來(lái)根本不像歸納法的版本。
良序原理:任何非負(fù)整數(shù)的非空集合都有一個(gè)最小的元素。
這個(gè)論斷看起來(lái)很明顯。如果S是一個(gè)大于或等于0的整數(shù)集合,并且S至少包含一個(gè)元素,那么其中之一必須是最小的。從數(shù)學(xué)基礎(chǔ)的角度來(lái)看,這個(gè)原理也需要證明。實(shí)際上它與數(shù)學(xué)歸納法是等價(jià)的。證明兩者之中的任何一個(gè)都需要深入探討“假設(shè)”這一元數(shù)學(xué)問(wèn)題,如果不按照這些原則,不難證明上述兩個(gè)原理(數(shù)學(xué)歸納法與良序原理)之間的相互蘊(yùn)含關(guān)系(習(xí)題4.8)。
借助于良序原理,我們可以證明定理1.5——算術(shù)基本定理,即每個(gè)大于1的整數(shù)n有唯一的質(zhì)分解式。
證明:對(duì)n做數(shù)學(xué)歸納。
歸納基礎(chǔ)。n0=2。顯然2=21,并且沒(méi)有其他指數(shù)為正的質(zhì)數(shù)的乘積可以等于2。
歸納假設(shè)。對(duì)于某個(gè)n≥2,假設(shè)對(duì)于每個(gè)m(2≤m≤n)有一個(gè)唯一的質(zhì)分解式。
歸納步驟。現(xiàn)在考慮n+1的情況。如果n+1是質(zhì)數(shù),那么n+1=(n+1)1是n+1的唯一質(zhì)分解式。如果n+1不是質(zhì)數(shù),那么設(shè)S是其所有大于1的因子的集合。根據(jù)良序原理,S有一個(gè)最小的元素p,它必為質(zhì)數(shù),否則p的任何因子都是n+1的比p更小的因子。設(shè)q=(n+1)/p,那么q≤n(實(shí)際上,q<n),因此根據(jù)歸納假設(shè),q具有唯一的質(zhì)分解式:
p要么是p1,要么是小于p1的質(zhì)數(shù),我們可以稱之為p0。在第一種情況下,有
在第二種情況下,有
我們將其作為一個(gè)練習(xí):證明任何數(shù)不存在一個(gè)以上的質(zhì)分解式(見(jiàn)習(xí)題4.7)。■
- 數(shù)字經(jīng)濟(jì):“數(shù)字中國(guó)”頂層規(guī)劃與實(shí)踐路徑
- 粵港澳大灣區(qū)觀察:帶你看清大灣區(qū)八大產(chǎn)業(yè)發(fā)展前景(《21世紀(jì)經(jīng)濟(jì)報(bào)道》深度觀察)
- 魔鬼數(shù)學(xué):大數(shù)據(jù)時(shí)代,數(shù)學(xué)思維的力量
- 數(shù)量經(jīng)濟(jì)研究(2018年/第9卷/第2期)
- 穿透數(shù)據(jù):經(jīng)濟(jì)數(shù)據(jù)理解要點(diǎn)與分析應(yīng)用(職業(yè)教育經(jīng)濟(jì)管理類新形態(tài)系列教材)
- 此算與彼算:圓錐曲線在清代
- 統(tǒng)計(jì)學(xué)
- 算力:數(shù)字經(jīng)濟(jì)的新引擎
- 數(shù)量經(jīng)濟(jì)研究(2017年/第8卷/第2期)
- 數(shù)量經(jīng)濟(jì)研究(2016年/第7卷/第2期)
- 定性數(shù)據(jù)的統(tǒng)計(jì)分析
- 數(shù)字化與數(shù)字經(jīng)濟(jì)
- 數(shù)學(xué)史講義概要
- 數(shù)量經(jīng)濟(jì)研究(2016年/第7卷/第1期)
- 走向數(shù)字經(jīng)濟(jì)