- 計算機科學中的離散數學基礎
- (美)哈瑞·劉易斯 雷切爾·扎克斯
- 1155字
- 2025-08-07 15:17:32
習題
3.1 求下列表達式的閉式表達式,見式(3-3)。
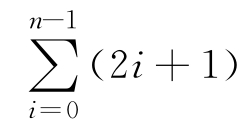
3.2 用歸納法證明鴿籠原理(例3.19),用|Y|代替|X|進行歸納。
3.3 用歸納法證明擴展鴿籠原理(定理1.3和定理1.4)。
3.4(a)使用∑表示對2的前n個奇數冪求和(即項為21、23等),并用歸納法證明其和是 。
。
(b)使用![]() 表示2的前n個負整數的冪的乘積(即因子為2-1、2-2等),求乘積的值。
表示2的前n個負整數的冪的乘積(即因子為2-1、2-2等),求乘積的值。
3.5 對于任意的n≥0,用歸納法證明
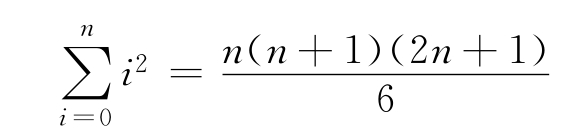
3.6 對于任意的n≥0,設
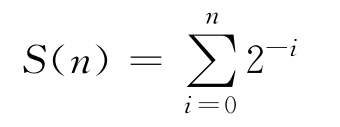
我們要證明S(n)總是小于2的,且當n足夠大時,它趨近于2。
(a)S(0)、S(1)、S(2)、S(3)都等于什么?
(b)推測S(n)的通用公式,形式如下:
S(n)=2-…
(c)用歸納法證明,該公式對于所有的n≥0都是正確的。
(d)設ε是一個非常小的正實數。n為多大時,S(n)可以達到2的ε鄰域內?
3.7 對于任意的n≥0,用歸納法證明
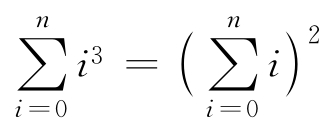
3.8 對于任意的n≥1,用歸納法證明

3.9 指出下面證明中的漏洞。
所有的馬都是相同的顏色。
歸納基礎。考慮只有一匹馬的集合。只有一匹馬意味著這匹馬和它自己是同樣顏色的,所以命題成立。
歸納假設。假設對于所有n≥1的馬的集合,所有的馬都是相同的顏色。
歸納步驟。證明“對于所有n+1匹馬的集合,在同一個集合中的所有馬都是相同的顏色”,設一個有n+1匹馬的集合如下:
H={h1,h2,…,hn,hn+1}
設H有兩個不同的子集:
A={h1,h2,…,hn}
B={h2,…,hn,hn+1}
由于A和B都是n個元素的集合,所以在每個集合中,所有馬都是相同顏色的。由于hn+1與h2的顏色相同(因為兩者都在B集合中),h2(也在A集合中)與A集合中的其他馬是相同的顏色。因此,hn+1和A集合中的所有馬是相同的顏色,所以H集合中的所有馬肯定都是相同的顏色。
因此,對于任意大小的馬的集合,同一集合中的所有馬都是相同的顏色。
3.10 如果相繼兩個元素之間的差每向后一步就會增加1,那么512真的會出現在求和公式(3-2)中最后一個數的位置上嗎?
3.11 證明下面有關Thue序列的結論。
(a)對于任意的n≥1,T2n是一個回文字符串(palindrome),即一個字符串正讀和反讀都是相同的。
(b)對于任意的n,如果同步將Tn中的0換為01、1換為10,可得到Tn+1。這意味著在無窮的Thue位串t0t1…中,也會同步發生上述替換,那么還會得到一個無窮的Thue位串。
3.12 證明:數學歸納法原理比實際需要更通用。也就是說,數學歸納法能證明的命題,弱數學歸納法原理也可以證明:
如果P(0)為真,并且對于任意的n,當P(n)為真時,P(n+1)為真,那么對于所有的n,有P(n)為真。
在數學歸納法中,當固定n0的值為0時,我們稱之為弱歸納法。
[1] 我們在公式中使用(2i+1)來表示項,括號的作用是避免歧義,即我們是對整個表達式求和,不是僅對其中的2i求和(見下式),此值與原式不相同。
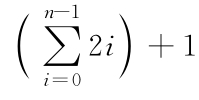
[2] 二進制數字,它們是小的信息塊。
[3] 以挪威數學家AxelThue(1863—1922)的名字命名,名字的發音為“Too-eh”。有時也稱之為Thue-Morse序列或Thue-Morse-Prohet序列,得名于美國數學家Marston Morse(1892—1977)以及法國數學家Eugène Prouhet(1819—1967)。早在1851年,Eugène Prouhet就使用了這個序列。