一、東西方最早的無(wú)窮觀念

數(shù)學(xué)意義上的無(wú)窮觀念，是數(shù)學(xué)思想擺脫了純粹應(yīng)用而走向思辨道路后產(chǎn)生的。以時(shí)間順序而言，對(duì)它的爭(zhēng)論最早出現(xiàn)于古希臘。總體上說(shuō)，古希臘人對(duì)無(wú)窮缺乏好感。阿那克西曼德（Anaximander）使用術(shù)語(yǔ)apeiron來(lái)表示自然世界之前的混沌世界，或者說(shuō)缺少形式和差異的某種虛空。古希臘人不喜歡這種虛空，很多自然哲學(xué)家為如何認(rèn)識(shí)無(wú)限所困擾，它究竟指的是物體的數(shù)量，還是組成物體的元素種類(lèi)，抑或元素組合的形式？對(duì)此大家眾說(shuō)紛紜，莫衷一是。公元前4世紀(jì)亞里士多德對(duì)無(wú)限進(jìn)行論述后，它在古希臘數(shù)學(xué)中逐漸獲得穩(wěn)定的意義。

畢達(dá)哥拉斯（Pythagoras）及其弟子們認(rèn)同無(wú)限是實(shí)際存在的，但有限（peras）不斷征服著無(wú)限，正如整數(shù)通過(guò)反復(fù)加1而持續(xù)增加。而以1個(gè)點(diǎn)出發(fā)向外擴(kuò)張的陣列，其形狀永遠(yuǎn)是一致的，去掉這個(gè)出發(fā)點(diǎn)后，其陣列則總是變換，但其長(zhǎng)寬仍可轉(zhuǎn)化為正整數(shù)之比。通過(guò)這種“數(shù)的可公度性”（commensurability），該學(xué)派企圖對(duì)無(wú)限加以限制。這一信念最終被無(wú)理數(shù)的發(fā)現(xiàn)所粉碎，因?yàn)橥ㄟ^(guò)反證法，可以證明正方形對(duì)角線和其邊長(zhǎng)不符合前述性質(zhì)。與之相對(duì)應(yīng)的，以德謨克利特（Democritus）為代表的“原子論”哲學(xué)認(rèn)為事物不是無(wú)限可分的，分割的盡頭是被稱(chēng)為“原子”的物質(zhì)微粒。但原子的組合方式無(wú)限，組成了無(wú)限數(shù)量的事物。(21)

公元前5世紀(jì)的愛(ài)利亞學(xué)派哲人芝諾（Zeno of Elea），提出了幾個(gè)著名的悖論，他的本意是捍衛(wèi)其老師巴門(mén)尼德（Parmenides）的“存在是一”的哲學(xué)思想，然而同時(shí)也破除了畢達(dá)哥拉斯學(xué)派對(duì)秩序的拘泥。其中最有名的一個(gè)悖論是：神話(huà)中善跑的英雄阿喀琉斯（Achilles）永遠(yuǎn)不可能追上烏龜，因?yàn)闉觚斂梢栽谌我鈺r(shí)刻制造一個(gè)起點(diǎn)，阿喀琉斯追到該起點(diǎn)時(shí)，烏龜已從這個(gè)起點(diǎn)走出一段距離，到達(dá)下一個(gè)起點(diǎn)。這樣不論距離有多小，只要烏龜一直往前爬，阿喀琉斯就永遠(yuǎn)困于追逐下一個(gè)起點(diǎn)，永遠(yuǎn)追不上已經(jīng)離開(kāi)這個(gè)起點(diǎn)的烏龜。在悖論中，芝諾挑戰(zhàn)了之前被奉為圭臬的可公度量——這個(gè)量仍然可以無(wú)限地劃分下去。芝諾悖論和無(wú)理數(shù)一道構(gòu)成了摧毀畢達(dá)哥拉斯體系的第一次數(shù)學(xué)危機(jī)。(22)

亞里士多德認(rèn)為，芝諾在悖論中混淆了事物分割的實(shí)體無(wú)限，以及大小兩個(gè)方向延伸或分割的潛在無(wú)限。有限的時(shí)間固然不能穿越無(wú)窮延伸的距離，卻可以越過(guò)有限量度，讓距離被無(wú)窮分割成無(wú)數(shù)個(gè)點(diǎn)而到達(dá)終點(diǎn)，而這有限的時(shí)間也同樣可以被無(wú)窮分割。具體到數(shù)學(xué)意義上，亞里士多德解釋說(shuō)，當(dāng)追趕者與被追者之間的距離越來(lái)越小時(shí)，追趕所需的時(shí)間也越來(lái)越小，無(wú)窮個(gè)越來(lái)越小的數(shù)加起來(lái)的和是有限的，所以可以在有限的時(shí)間內(nèi)追上。亞里士多德承認(rèn)并規(guī)范了無(wú)窮的范疇，是哲學(xué)家對(duì)芝諾悖論的最早回應(yīng)，但他在數(shù)學(xué)上的解答卻不準(zhǔn)確，我們很容易就他的猜想“無(wú)窮個(gè)越來(lái)越小的數(shù)之和為有限”找出反例。例如調(diào)和級(jí)數(shù)1+1/2+1/3+1/4+…的每一項(xiàng)都遞減，可是它的和卻是發(fā)散的。直到公元前3世紀(jì)，阿基米德（Archimedes）才明確給出“阿喀琉斯與烏龜”悖論中所涉及之幾何級(jí)數(shù)的計(jì)算方法，他計(jì)算出無(wú)窮數(shù)列之和為，當(dāng)n趨于無(wú)窮大時(shí)，結(jié)果等于4/3。由此，阿基米德從數(shù)學(xué)角度給出了解決芝諾悖論的途徑。(23)

可以與古希臘作為比較的是中國(guó)先秦時(shí)期諸子思想中的無(wú)窮觀念。《莊子》記載惠施說(shuō)：“至大無(wú)外，謂之大一；至小無(wú)內(nèi)，謂之小一”，認(rèn)為“至大”沒(méi)有外邊界，而“至小”沒(méi)有內(nèi)邊界，這是空間無(wú)限大和無(wú)窮小的明確敘述。對(duì)無(wú)窮觀念表述更加淋漓盡致的是《墨經(jīng)》，該書(shū)對(duì)諸多概念進(jìn)行了明確定義，其中就包括“窮，或有前不容尺也”，“窮，或不容尺，有窮；莫不容尺，無(wú)窮也”這樣的命題，即如果用尺來(lái)丈量的話(huà)，若前方已不夠一尺，則這里就是“有窮”，但如若無(wú)論量至何處，前面總還有一尺的余量，這就是“無(wú)窮”。由此可以判定空間在各個(gè)方向上有限或無(wú)限的性質(zhì)。另一方面，除了大到無(wú)限的思想，墨家還提出“端”、“始”等概念，反映了無(wú)窮小的時(shí)空觀。它們都是一個(gè)存在物，可以由連續(xù)不斷的分割得到，其量度為零，并且具有可積性。(24)其中，“端”的含義是將一個(gè)長(zhǎng)條狀的東西每次割去一半，最后達(dá)到不能再分割成半的時(shí)候，便得到“端”，這與德謨克利特的原子論有相似之處。總體來(lái)看，墨家對(duì)無(wú)限的認(rèn)識(shí)與古希臘的實(shí)體無(wú)限有相近之處。與“端”相對(duì)的是墨家的辯論對(duì)手——名家的觀點(diǎn)：“一尺之棰，日取其半，萬(wàn)世不竭。”墨家的“端”更像是從經(jīng)驗(yàn)抽象得出，似乎沒(méi)有考慮分割次數(shù)（過(guò)程）的無(wú)限，而名家論辯的重點(diǎn)則是過(guò)程的無(wú)限導(dǎo)致結(jié)果的無(wú)窮小。他們的命題僅留下觀點(diǎn)，缺乏詳細(xì)論證，今天看來(lái)是無(wú)從也無(wú)需辯駁的。(25)

墨家在戰(zhàn)國(guó)時(shí)期曾顯赫一時(shí)，但漢代之后漸不為人所知。對(duì)中國(guó)后世數(shù)學(xué)思想影響更大的是道家對(duì)無(wú)窮的論說(shuō)。在老莊哲學(xué)中，無(wú)限和有限之間存在著清晰的界限。積微當(dāng)然可以成著，但形成的“合抱之木”、“九層之臺(tái)”及“千里之行”等都是顯著有限可量的事物。對(duì)于“不見(jiàn)水端”、“不可為量數(shù)”的北海，就無(wú)法以有限的“萬(wàn)川”、“尾閭”等體積在“不知何時(shí)止”這有限時(shí)間內(nèi)充填或排空。“無(wú)形者，數(shù)之所不能分也；不可圍者，數(shù)之所不能窮也”，也就是說(shuō)，任何有限個(gè)有限量之和都不能達(dá)到無(wú)限量，無(wú)限和有限之間存在鴻溝。道家對(duì)無(wú)限量進(jìn)行闡述的目的，在于說(shuō)明“道”所兼有的無(wú)窮大和無(wú)窮小特性：“道近乎無(wú)內(nèi)，遠(yuǎn)乎無(wú)外”，“道”可生“一”，這里的“一”當(dāng)然不是指數(shù)量上的1，而是象征由道所生而萬(wàn)物所由生的東西。在某些方面，老子哲學(xué)將無(wú)限和世界本原相聯(lián)系，與古希臘巴門(mén)尼德的后學(xué)們由“存在是一”推演出可使無(wú)限容身的悖論，是一個(gè)值得進(jìn)行比較的有趣話(huà)題。隨著道論被知識(shí)階層廣泛接受，“一”逐漸與萬(wàn)物根源“太一”或“道”混同起來(lái)。魏晉時(shí)期，老莊哲學(xué)的注釋家又逐漸把數(shù)字的概念摻入“一”，如王弼就說(shuō)“一，數(shù)之始而物之極也”，這對(duì)中國(guó)古代大數(shù)學(xué)家劉徽“一者數(shù)之母”觀念的提出產(chǎn)生了重要影響。(26)

無(wú)限思想的另一源頭是印度耆那教。印度數(shù)學(xué)的一個(gè)特點(diǎn)是對(duì)大數(shù)記數(shù)法的偏愛(ài)，這些大數(shù)被用來(lái)度量時(shí)間和空間。在吠陀時(shí)代就發(fā)展出高至1012的數(shù)位名稱(chēng)（稱(chēng)為parārdha）。而在佛教典籍《方廣大莊嚴(yán)經(jīng)》中，數(shù)位達(dá)到1053（稱(chēng)為怛羅絡(luò)叉tallak?a?a），此外還有表示10140的阿僧（asankhyeya）等。這些大數(shù)量的引入導(dǎo)致耆那教思想中逐漸形成無(wú)限的數(shù)字體系。在成書(shū)于公元前4—前3世紀(jì)的耆那教《波羅聶提經(jīng)》（Surya Prajnapti）中，把數(shù)字分為三類(lèi)：“可計(jì)的”（sa?khyeya）、“不可計(jì)的”（asa?khyeya）以及“無(wú)限的”（ananta）。每一類(lèi)又再序分為三類(lèi)，“不可計(jì)的”和“無(wú)限的”的次一類(lèi)之下再各序分為三類(lèi)，因此共計(jì)21類(lèi)。其中可計(jì)的數(shù)字有“最低的”（只有2）、“中等的”（從3到a-2）和最高的（a-1），其中a對(duì)應(yīng)于現(xiàn)代數(shù)學(xué)中的能夠與自然數(shù)集合一一對(duì)應(yīng)的可數(shù)集₀，它可以表示任意包含無(wú)限（即“不可計(jì)的”）元素的有理數(shù)集合。(27)隨后“不可計(jì)的”中最低的“接近不可計(jì)的”就包含從a，a+1直到b-1（b=aa），由此我們可以列出如下耆那教所設(shè)想的數(shù)字分類(lèi)：(28)

續(xù)表

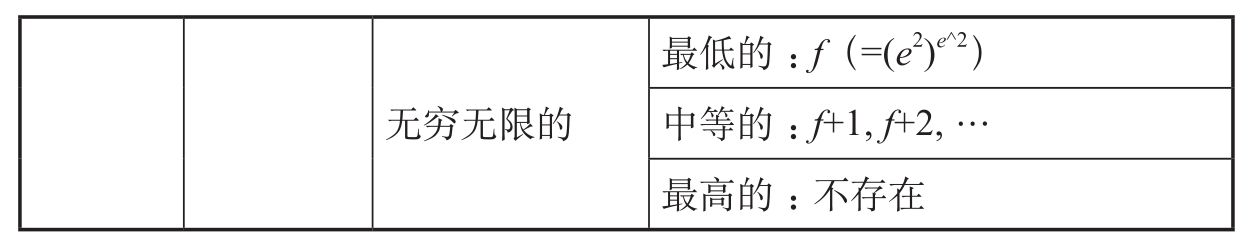
對(duì)于這些令人眼花繚亂到驚嘆地步的計(jì)數(shù)方法，耆那教有可能曾經(jīng)發(fā)展出一套記數(shù)符號(hào)系統(tǒng)，因?yàn)樵谄浣?jīng)典中曾經(jīng)用ankalipi和ga?italipi兩個(gè)詞來(lái)表示不同計(jì)數(shù)的書(shū)寫(xiě)，這兩個(gè)詞有可能一個(gè)表示鐫刻，而另一個(gè)表示常規(guī)書(shū)寫(xiě)。另外，耆那教計(jì)數(shù)體系中各類(lèi)別的分野，又很容易讓人聯(lián)想到古希臘大數(shù)學(xué)家阿基米德在《算沙者》（The Sand Reckoner），以及阿波羅尼烏斯（Apollonius of Perga）關(guān)于不同級(jí)別數(shù)位的換算論述。耆那教計(jì)數(shù)體系與古希臘數(shù)學(xué)各有其文化背景，它們之間是否存在相互影響的關(guān)系引起不少學(xué)者興趣，但目前尚無(wú)定論。(29)