- 絲綢之路上的科學技術
- 王陽 陳巍
- 1751字
- 2023-04-11 18:47:45
二、巴比倫數表是否意味著畢達哥拉斯定理的發現?
上述關于古代中國勾股定理與古希臘畢達哥拉斯定理的三個層次分析,已經展現出數學定理的復雜性。這只是限于以往材料的理解,如果我們充分重視兩則新材料,一是巴比倫泥版Plimpton 322號的研究狀況,二是曲安京等人關于周髀算經中商高與周公對話的新闡釋,勾股定理的中西比較呈現出更為有趣的中西文化差異,以及關于數學本質的復雜理解。
第一則材料是美國哥倫比亞大學所藏的Plimpton 322號巴比倫泥版。在20世紀之前,西方學者相信,古希臘畢達哥拉斯學派是在埃及文明的基礎上發展出證明的方法,而沒有注意到巴比倫人已經取得了令人驚訝的數學成就。比如,數學史家克萊因謹慎地寫道:“我們也不知道埃及人是否認識到畢達哥拉斯定理。我們知道他們有拉繩人(測量員),但所傳他們在繩上打結,把全長分成長度各為3、4、5的三段,然后用來形成直角三角形之說,則從未在任何文件上得證實。”(8)丹皮爾(W. C. Dampier)認為:“歐幾里德幾何學第一冊的第四十七命題現在還稱為畢達哥拉斯定理。畫直角的‘繩則’也許早已在埃及和印度憑經驗發現了,但是,很可能到畢達哥拉斯,才第一次用演繹的方法證明直角三角形斜邊的平方等于它兩邊平方之和。”(9)
1945年,美國數學史家諾伊格鮑爾(Otto Neugebauer)細致考察了Plimpton 322號泥版,考證出巴比倫人在漢穆拉比時代(約前1700)已經發現畢達哥拉斯數組,并且達到極高的程度,由此激發起關于畢達哥拉斯數組究竟是特例表述還是普遍性表述,到底是代數表述還是具有幾何學意義的一系列新的問題。這塊泥版有15行、4列數字。巴比倫是六十進制,它可以換算為十進制;巴比倫是從右邊向左邊書寫數表。

圖1-1 Plimpton 322號泥版(哥倫比亞大學藏)
如下是筆者根據巴克(Creighton Buck)論文(10)換算而編制的數表:
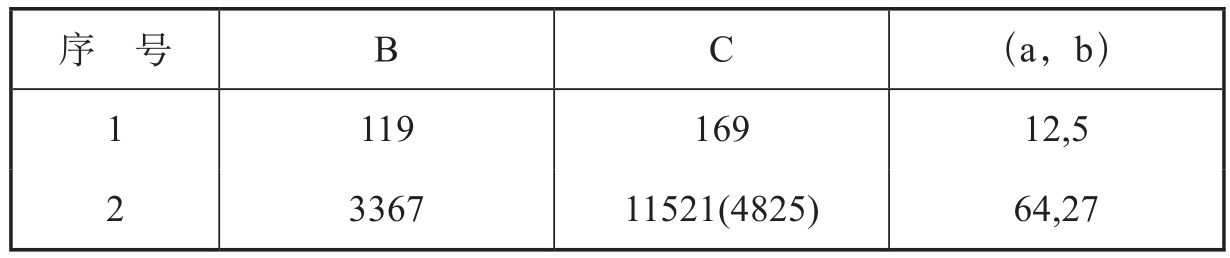
續表
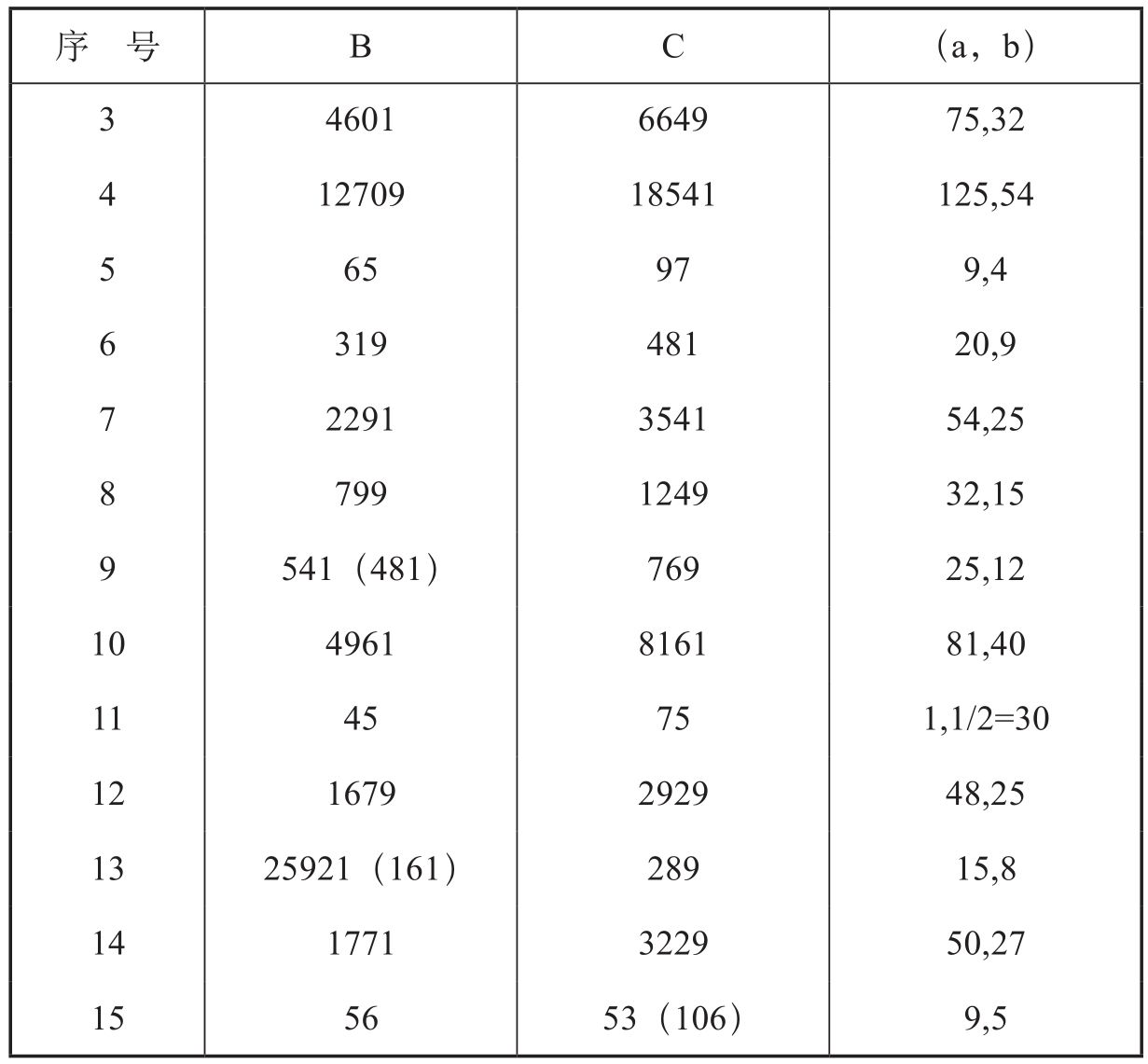
諾伊格鮑爾發現:第3列數(C)與第2列數(B)的平方差都是平方數,如:1692-1192=1202(第1行),最大的是185412-127092=135002(第4行)。泥版只有四處不滿足這一規律,猜測是祭司抄寫錯誤所致(表中括號內為錯誤數字,旁邊添加了正確數字)。巴克認為,如果C+B=2a2,C-B=2b2,那么a和b的數值如數表最后一列所示。由此,B=a2-b2,C=a2+b2。令D=2ab,就形成了畢達哥拉斯數組,如下圖所示。

如果以定理的普遍性表述作為定理發現的標準,巴比倫數表算不算畢達哥拉斯定理的發現呢?這里涉及兩個問題,一是巴比倫數表是否暗含著普遍性的表述?二是巴比倫數表是否具有幾何學意義?
關于第一個問題,上述巴比倫數表很有可能是用于幫助進行算學訓練的泥版。高達萬位的巴比倫數表已經不具有丈量土地等實用意義,它無法純粹通過實踐去測量達到。或許到百位的勾股數,甚至千位,都有可能依靠經驗進行估算,高達萬位的勾股數需要極其巨大的計算量,僅僅依靠日常經驗的估算這幾乎是難以達到的。
進一步的問題是,高達萬位的勾股數是怎么計算出來的呢?有沒有可能暗含著勾股定理的普遍性表述呢?筆者認為,高達萬位的多個勾股數不可能偶然地計算出來,巴比倫人沒有明確地闡明c2=a2+b2的普遍性表述,并不能夠否定他們知道c2=a2+b2,清楚平方的概念,否則,這些無法借助直接測量的量是不可能計算出來的。
關于第二個問題,即便巴比倫數表暗含著巴比倫人掌握了c2=a2+b2的普遍性表述,這僅是一個代數數組,還是一個幾何定理?如果僅是一個代數數組,能否稱之為畢達哥拉斯定理呢?麥金農(Nick Mackinnon)使用了巴比倫時期的另外一塊泥版(如下圖所示),表明了巴比倫借助幾何技巧幫助實現數學求解。(11)巴比倫數組的意義很可能在于幫助設計或者求解與直角三角形有關的方程或者代數問題。克萊因在巴比倫數表發現前就相信,埃及人和巴比倫人只是把幾何作為實用工具,“埃及人的幾何是怎樣的呢?他們并不把算術和幾何分開,草片文書中都有這兩方面的問題。埃及人也像巴比倫人那樣,把幾何看作實用工具。他們只是把算術和代數用來解有關面積、體積及其他幾何性質的問題”。(12)
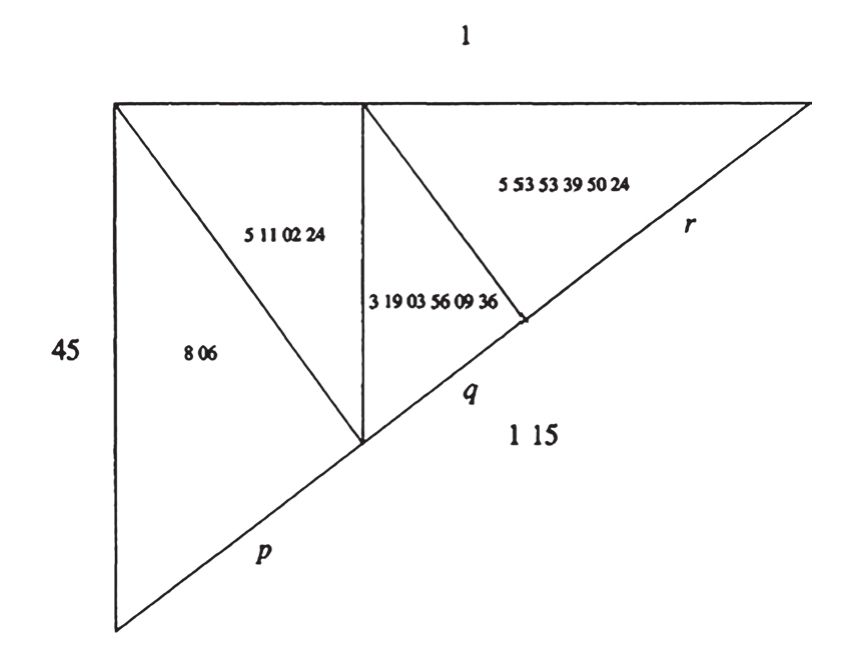
巴比倫人沒有明確表述巴比倫數表的幾何意義,他們又確實利用了幾何圖形幫助理解巴比倫數表。在西方思想傳統中,它實質是代數而不是幾何。在筆者看來,畢達哥拉斯定理的表述未必應當以代數和幾何的明確區分為標準,這只是表明數表的用途和目標,巴比倫人的上述幾何圖形暗含著畢達哥拉斯定理的表述。
概言之,巴比倫數表暗含著畢達哥拉斯定理的普遍性表述,其幾何圖形的運用暗含著畢達哥拉斯定理的幾何意義。筆者傾向于認為巴比倫人已經掌握了關于畢達哥拉斯定理的基本觀念。