3.2.2　對偶空間和對偶向量

向量的內積是一個函數，從同一空間取出兩個向量v和w，并計算得到一個數，記為。

以Dirac符號定義的對偶空間和對偶向量有如下定義：

設H為Hilbert空間，Hilbert空間H*定義為線性映射的集合，定義空間H*的向量和，并有。也就是說，空間H中兩個向量的內積屬于空間H*，其中是同屬于H空間的和的內積。

空間H*本身是一個復向量空間，稱為與H相關聯的對偶空間；是的對偶向量，是從中獲取相應的行矩陣后，取每個元素的復共軛（埃爾米特共軛）得到的。

兩個向量和的內積為，計算方法是以為行向量，為列向量，對應的元素乘積得到矩陣。例如，，，則兩者內積為：

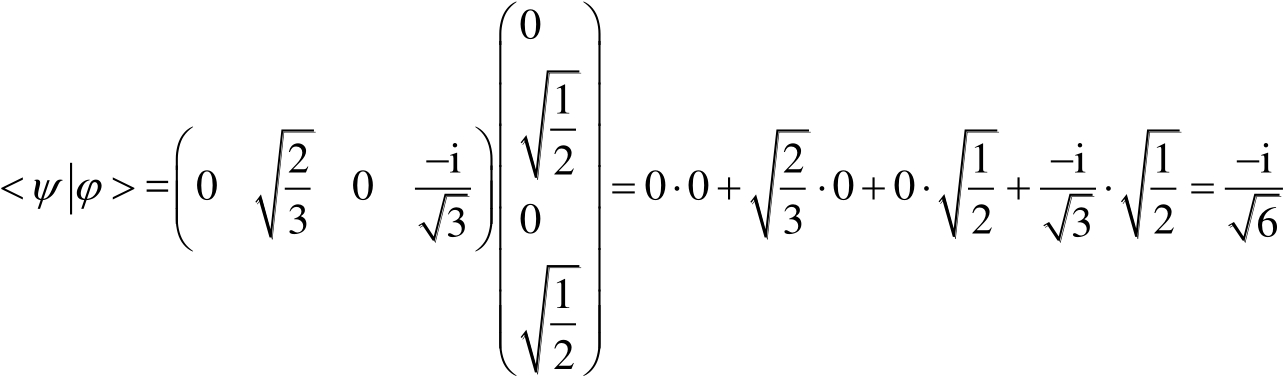
注意：此處的共軛是。如果兩個向量的內積為零，則稱其為正交向量。

的歐氏范數表示為，是它與自身內積后做平方根，即，范數為1的向量稱為單位向量，一組相互正交的單位向量稱為正交集。

考慮一個維數為的Hilbert空間H，當有且，當，則個組成空間H的一組正交基。例如就是一組滿足任意兩個向量內積為0、每個向量范數為1的一組正交基。按照該規則重新計算，的內積，有：