2.2 信息量和信息熵
2.2.1 信息量
所謂信息量就是信息多少的量度。假設(shè)信源發(fā)送方A發(fā)送消息給接收方B,所發(fā)出的消息是隨機(jī)的,在消息收到之前,接收方不能確定會收到什么消息,也就是無法消除消息的不確定性,這種不確定性越大,接收方B在收到完整消息時所獲得的信息量就越大;如果消息在傳輸過程中受到干擾,導(dǎo)致接收方B對收到消息的不確定性減小甚至不確定性沒有改變,那么獲得的信息量就較少或者信息量為零。下面舉幾個簡單例子來說明。
“太陽今天早晨竟然從東邊升起!”
“吸煙有害健康!”
“天冷要多穿衣服!”
當(dāng)你看到上面幾個消息時,你一定會覺得很無聊,因?yàn)槲覀兌贾肋@些事情,它們發(fā)生的概率幾乎為1,所以沒有多少信息。
假如你看的新聞標(biāo)題是:“中國男籃30分大勝美國夢之隊(duì)”“中國足球隊(duì)5比0大勝巴西隊(duì)”,你會立刻產(chǎn)生興趣,因?yàn)檫@些事情發(fā)生的可能性太小。因此,一件事情包含的信息和它發(fā)生的概率成負(fù)相關(guān)關(guān)系(即概率越大信息越少,概率趨近于0,信息趨近于無窮大),信息量的大小跟這種信息不確定的消除有關(guān)。
那么可以定義信息量為:
信息量=不確定性減少量(消息收到前的不確定性-消息收到后的不確定性)
當(dāng)沒有干擾時,收到信息后的不確定性為零,那么此時獲得的信息量=消息發(fā)出前的不確定性,也可以認(rèn)為是信源消息所含有的信息量。用公式來表示的話,就是某件事發(fā)生所含有的信息量等同于該事件發(fā)生的先驗(yàn)概率函數(shù)

式中,P(xi)是事件xi發(fā)生的先驗(yàn)概率,而I(xi)表示事件xi發(fā)生所含有的信息量,稱之為xi的自信息量。
按照剛才的分析,函數(shù)f[P(xi)]應(yīng)該滿足如下條件:
(1)f[P(xi)]與概率P(xi)負(fù)相關(guān),即當(dāng)P(x1)>P(x2)時,f[P(x1)]<f[P(x2)]。
(2)P(x1)=1,那么f[P(x1)]=0。
(3)P(x1)=0,那么f[P(x1)]=∞。
(4)I(AB)=I(A)+I(B),即兩個毫不相關(guān)的事件A和事件B同時發(fā)生所提供的信息量等于兩個事件各自發(fā)生的信息量之和。
1928年R.V.L.哈特萊首先提出信息定量化的初步設(shè)想,他將消息數(shù)的對數(shù)定義為信息量。從數(shù)學(xué)上可以證明對數(shù)形式能夠滿足剛才所提條件。若信源有p種消息,且每個消息是以相等可能產(chǎn)生的,則該信源的信息量可表示為

其中,p為事件發(fā)生的概率,I為該事件的自信息量。如果對數(shù)的底取為2,那么就是最常見的信息度量,單位為比特(bit),如果取自然對數(shù)的底e,那么單位為奈特(nat),如果底數(shù)取為10,那么單位為哈特(hart),通常情況下,都采用以2為底的對數(shù)。
由上式可以看出一種特殊情況:若p=1/2,那么I=1bit,也就是二選一時的信息量。這也說明了二元數(shù)字所能提供的信息量為1bit。
自信息量只是表征信源本身的信息特征,但在一般的通信系統(tǒng)里,信源、信道和信宿必須整體進(jìn)行考慮。假設(shè)信源輸出為X,信宿輸入為Y,如圖2-1所示,那么通常表示某事件在某種條件下出現(xiàn),這時所帶來的信息量就需要在X、Y集合中進(jìn)行考慮,并且要用條件概率來進(jìn)行描述。

圖2-1 信息系統(tǒng)模型
假設(shè)在y條件下,隨機(jī)事件x的條件概率為P(x|y),則x的出現(xiàn)所引發(fā)的信息量稱為

反之,在x條件下,y所帶來的信息量也是條件自信息量:

對于通信系統(tǒng)而言,該條件概率只與信道特性有關(guān),因此上述條件自信息量可以看作是信道給出的信息量。
接下來看第三個概念:互信息量。
對兩個離散隨機(jī)事件集合X和Y,事件yi的出現(xiàn)給出關(guān)于事件xi的信息量,定義為事件xi和yi的互信息量I(xi;yi),其表達(dá)式又分為兩種情況。
第一種,信道沒有干擾,信宿能夠完全獲取信源發(fā)出的信息量,那么

第二種,信道有干擾,信宿所受到的信息中有干擾信息,那么按照之前條件自信息量分析可知,此時
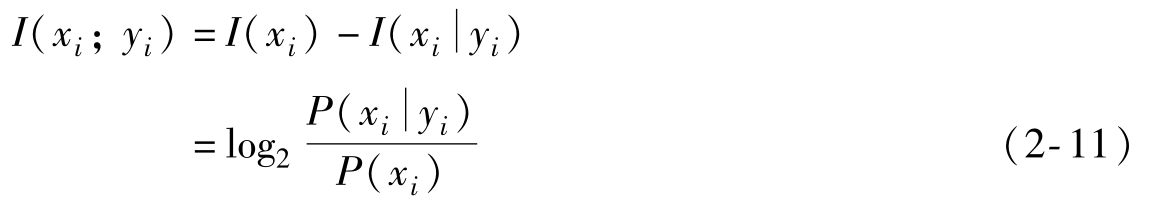
互信息量的性質(zhì)有如下三條:
(1)對稱性
由上式可以分析事件xi的出現(xiàn)給出關(guān)于事件yi的信息量,可以得到:
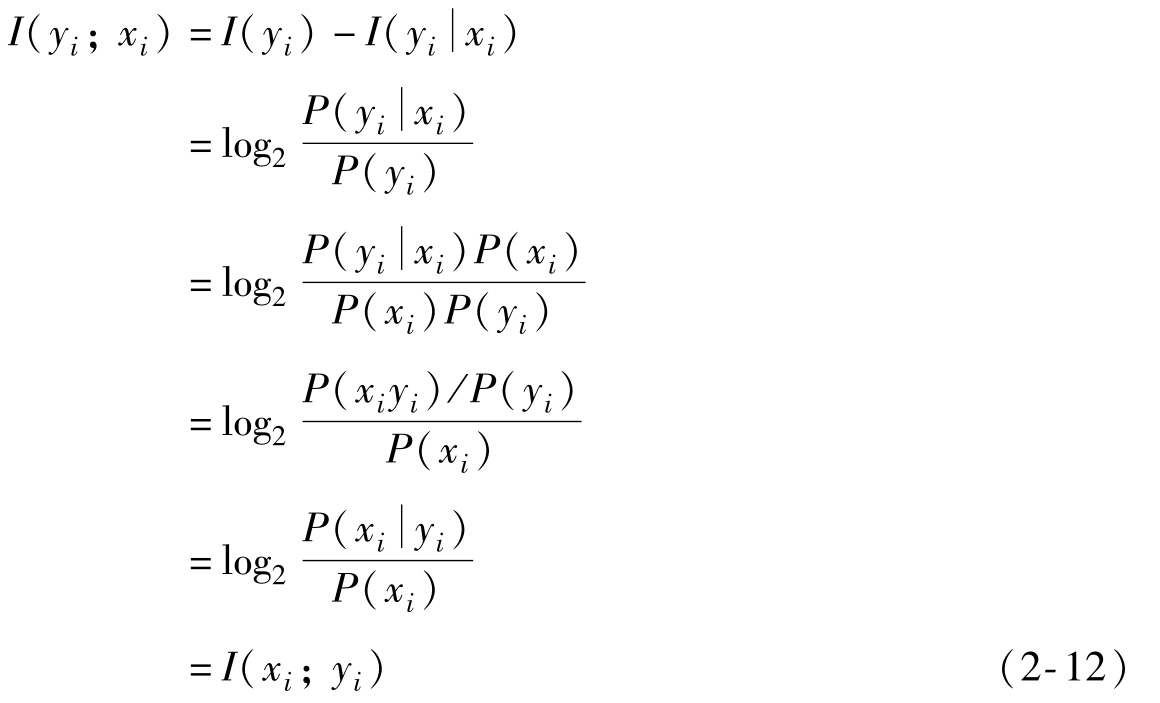
即I(xi;yi)=I(yi;xi),稱為互信息量的對稱性。
從上式還可以得到,P(xi)和P(yi)是事件發(fā)生的先驗(yàn)概率,而 和
和 是后驗(yàn)概率,那么:
是后驗(yàn)概率,那么:

這說明互信息量描述了兩個隨機(jī)事件之間的統(tǒng)計約束程度,如果先驗(yàn)概率已確定,后驗(yàn)概率就決定了信息的流通。
(2)值域?yàn)閷?shí)數(shù)
互信息量的值可以為正數(shù)、零或者負(fù)數(shù),按照其定義公式,可以分為幾種情況進(jìn)行討論:
1) ,那么I(xi;yi)=I(xi)。
,那么I(xi;yi)=I(xi)。
后驗(yàn)概率為1,說明信宿獲得了信源全部信息量,即信道沒有干擾。
2)P(xi)< <1,那么I(xi)>
<1,那么I(xi)> ,
, >0。
>0。
后驗(yàn)概率大于先驗(yàn)概率,說明收到事件yi能夠消除一些關(guān)于信源是否發(fā)生事件xi的不確定度,就是說yi獲得了關(guān)于xi的信息量。這也說明,雖然信道有干擾,信宿仍然可以從信源中獲取信息量。
3) =P(xi),那么I(xi;yi)=I(xi),
=P(xi),那么I(xi;yi)=I(xi), =0。
=0。
后驗(yàn)概率等于先驗(yàn)概率,說明收到事件yi對于信源是否發(fā)生事件xi沒有影響,就是說從yi那里無法獲得關(guān)于xi的信息量,也就是說yi與xi無關(guān)。
4)0< <P(xi),那么I(xi)<
<P(xi),那么I(xi)< ,
, <0。
<0。
后驗(yàn)概率小于先驗(yàn)概率,說明收到事件yi后對于信源是否發(fā)生事件xi有負(fù)影響,就是說雖然給出了信息量,但不是關(guān)于xi的信息量。
(3)不大于其中任一事件的自信息量
由于 ≤1,那么
≤1,那么
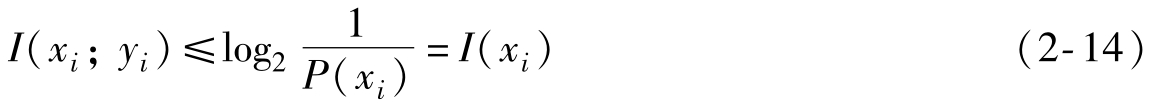
同理 ≤1,那么
≤1,那么
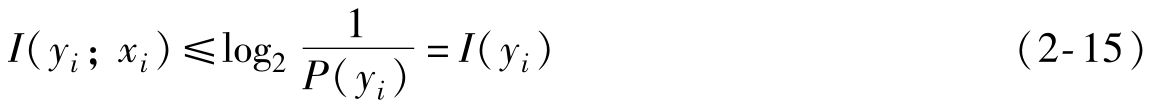
說明互信息量是描述信息流通的物理量,流通量的數(shù)值不能大于被流通量的數(shù)值。同時也說明某事件的自信息量是其他事件所能提供該事件的最大信息量。
最后來看第四個概念:平均互信息量。
互信息量只能定量地描述信源中發(fā)出某個消息xi,信宿中出現(xiàn)某一消息yi時,流經(jīng)信道的信息量,不能作為信道上信息流通的整體測度。如果要從整體的角度并且在平均意義上來度量信宿每接收到一個符號而從信源獲取的信息量,那么就要引入平均互信息量這個概念。
兩個離散隨機(jī)事件集合X和Y,若任意兩事件間的互信息量為I(xi;yi),則其聯(lián)合概率加權(quán)的統(tǒng)計平均值,稱為兩集合的平均互信息量,用I(X;Y)表示。
當(dāng)信宿收到某一符號yi后,從中獲得關(guān)于輸入符號的平均信息量,應(yīng)該是在條件概率空間中的統(tǒng)計平均,用I(X;yi)表示:
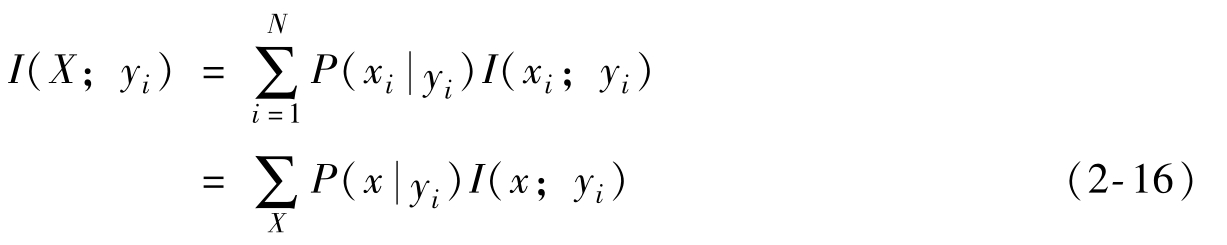
再對其在集合Y中取統(tǒng)計平均,得到
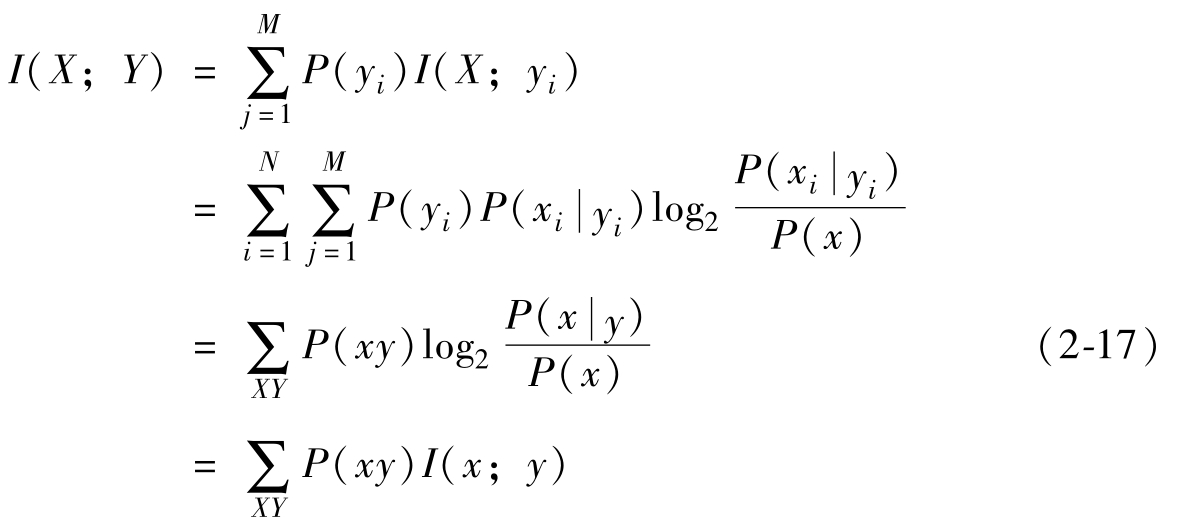
上式即是平均互信息量的數(shù)學(xué)表達(dá)式。
2.2.2 信息熵
一個信源的信息量有多少,很大程度上就是由它輸出的多種情況及各種情況的概率分布所決定的。信源發(fā)出的消息xi不同,其發(fā)生的概率P(xi)也不同,那么它們所含有的信息量I(xi)就會不同,因此自信息量I是一個隨機(jī)變量,不能作為整個信源的總體信息測度。如果要描述信源整體的信息量,那么應(yīng)該是信源各個不同符號xi(i=1,…,N)所包含的自信息量I(xi)在信源概率空間P(X)={P(x1),P(x2),…,P(xN)}中的統(tǒng)計平均值,稱之為平均自信息量,即
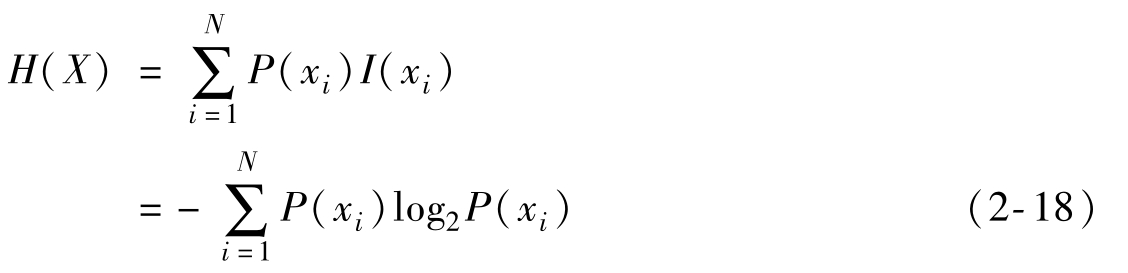
該表達(dá)式與熱力學(xué)中的熵表達(dá)式類似。熵在熱力學(xué)中的意義是不確定度。1948年,香農(nóng)(Shannon)在他著名的論文《通信的數(shù)學(xué)原理》中指出:“信息是用來消除隨機(jī)不確定性的東西”,并提出了“信息熵”的概念(借用了熱力學(xué)中熵的概念),來解決信息的度量問題。在信息論中將上式中的H稱為信息熵。對于單符號離散信源,信息熵是信源每發(fā)一個符號所提供的平均信息量,量綱為信息單位/信源符號。如果選取以r為底的對數(shù),那么信息熵選用r進(jìn)制單位,即
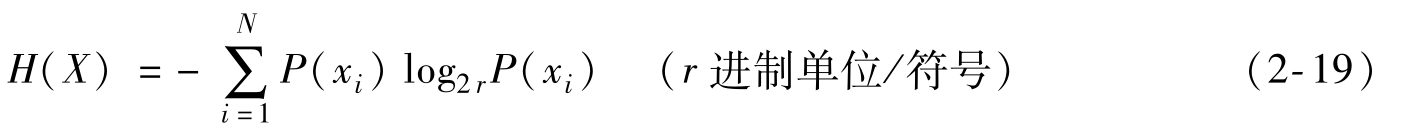
其中變量X指某隨機(jī)變量的整體,如果選以2為底的對數(shù),信息熵的單位是比特/符號。
我們以最簡單的單符號二元信源為例進(jìn)行說明,該信源僅取0和1兩個元素,那么其概率為p和1-p,其熵為:
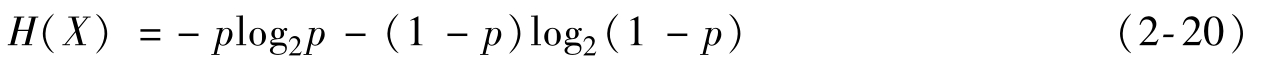
當(dāng)p=0或1時,H(X)=0,當(dāng) 時,H(X)=1。圖2-2給出了二進(jìn)制熵函數(shù)的曲線。
時,H(X)=1。圖2-2給出了二進(jìn)制熵函數(shù)的曲線。
由圖可見,離散信源的信息熵具有:
1)非負(fù)性,即收到一個信源符號所獲得的信息量應(yīng)為正值,H(X)≥0。
2)對稱性,即對稱于p=0.5。
3)確定性,H(1,0)=0,即p=0或p=1已是確定狀態(tài),所得信息量為零。
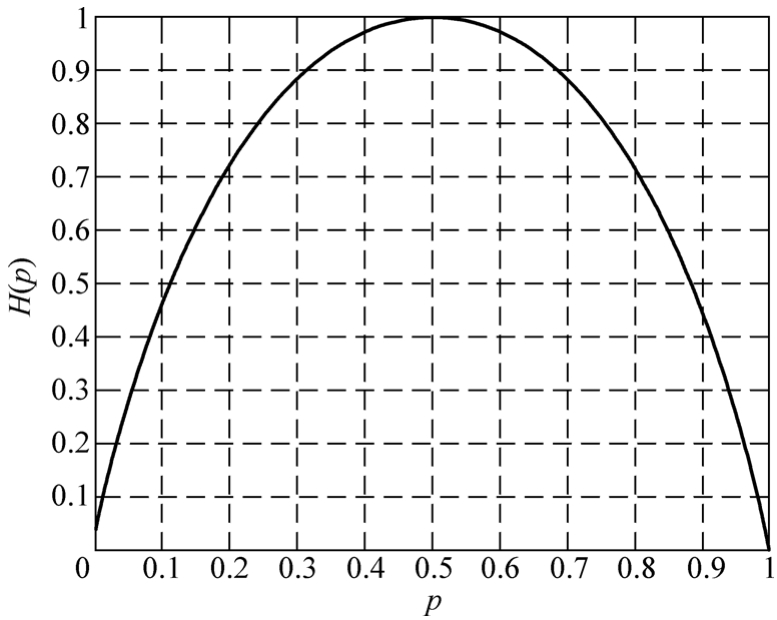
圖2-2 二進(jìn)制熵函數(shù)
4)極值性,當(dāng)p=0.5時,H(X)最大;而且H(X)是p的上凸函數(shù)。
【例2-1】看一個信息熵的例子,假設(shè)世界杯決賽圈32強(qiáng)已經(jīng)產(chǎn)生,那么隨機(jī)變量“世界杯足球賽32強(qiáng)中,誰是世界杯冠軍?”的信息量是多少呢?
【解】根據(jù)香農(nóng)給出的信息熵公式,對于任意一個隨機(jī)變量X,它的信息熵定義如下,單位為比特/符號:
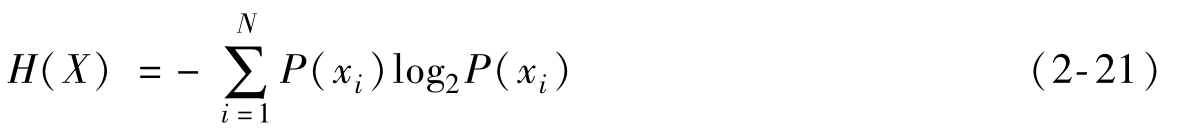
那么上述隨機(jī)變量(誰獲得冠軍)的信息量是:
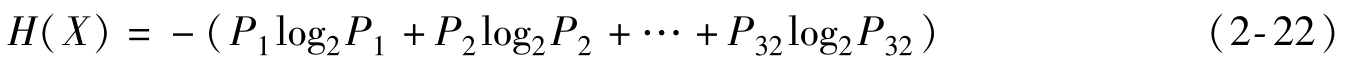
其中,P1,…,P32分別是這32強(qiáng)球隊(duì)奪冠的概率。
容易驗(yàn)證,以下幾個結(jié)論成立:
1)32強(qiáng)球隊(duì)奪冠概率相同時,H=5。
2)奪冠概率不同時,H<5。
3)H不可能大于5。
對于第一個結(jié)論,結(jié)果是很顯然的,奪冠概率相同,即每個球隊(duì)奪冠概率都是1/32,所以
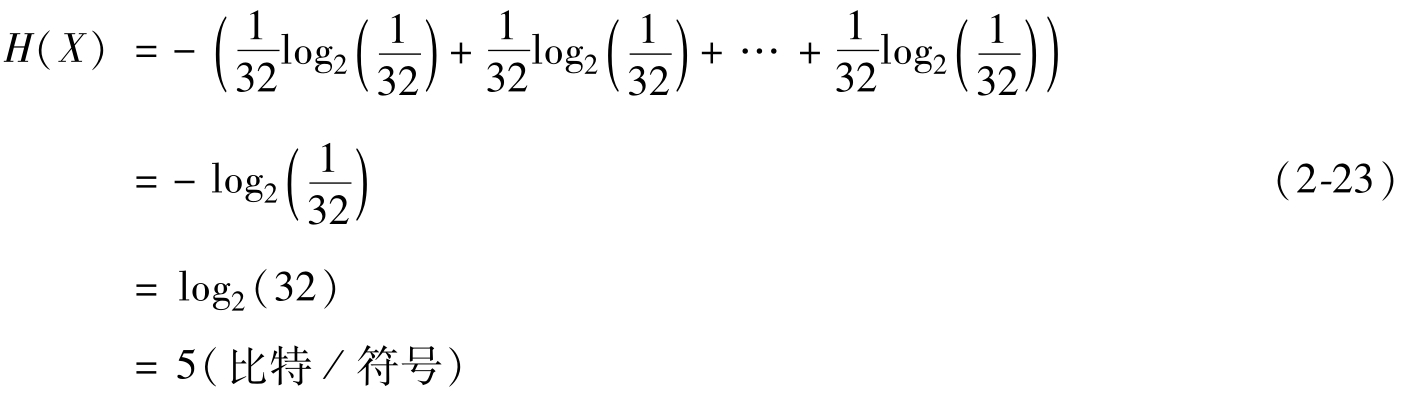
對于第二個和第三個結(jié)論,可以使用拉格朗日乘子法進(jìn)行證明。這實(shí)際上是說系統(tǒng)中各種隨機(jī)性概率越均等,信息熵越大,反之熵越小。
【例2-2】再來看一個比賽例子,假設(shè)有4個選手A、B、C、D,獲勝概率分別為1/2、1/4、1/8和1/8。接下來,將哪一選手獲勝視為一個隨機(jī)變量X∈{A,B,C,D}。假定需要用盡可能少的二元問題來確定隨機(jī)變量X的取值。
比如:問題1:A獲勝了嗎?問題2:B獲勝了嗎?問題3:C獲勝了嗎?最后可以通過最多3個二元問題,來確定X的取值,即哪一個選手贏了比賽。
如果X=A,那么需要問1次(問題1:是不是A?),概率為1/2;
如果X=B,那么需要問2次(問題1:是不是A?問題2:是不是B?),概率為1/4;
如果X=C,那么需要問3次(問題1,問題2,問題3:是不是C?),概率為1/8;
如果X=D,那么同樣需要問3次(問題1,問題2,問題3),概率為1/8。
那么很容易計算,在這種問法下,為確定X取值,需要的二元問題數(shù)量為:
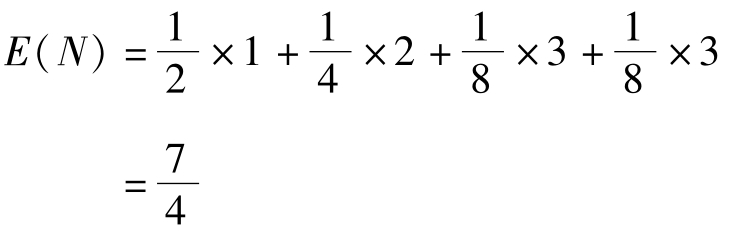
如果按照信息熵的定義,可以得到:
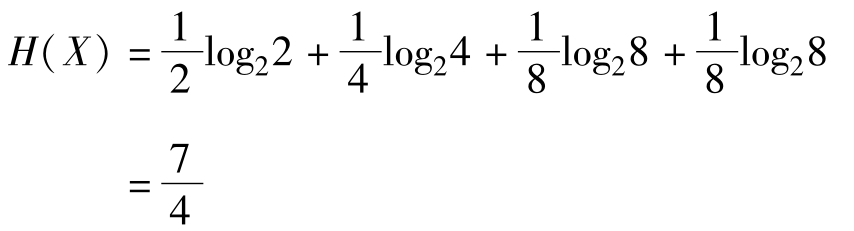
前面分析過,在二進(jìn)制中,一個比特為0或1,就代表了一個二元問題的答案。那么在計算機(jī)中給哪一位選手奪冠這個事件進(jìn)行編碼,所需要的平均碼長為1.75個(7/4個)比特。很顯然,為了盡可能減少碼長,要給發(fā)生概率較大的事件,分配較短的碼長,深入討論這個問題就可以得出霍夫曼編碼的概念。
例如本例題中,對于{A,B,C,D}四個選手,可以分別由{0,10,110,111}來表示,如果把最短的碼“0”分配給發(fā)生概率最高的A,碼“10”分配給B,以此類推,得到的平均碼長為1.75bit。但是如果反過來,給A分配最長的碼“111”,以此類推,那么平均碼長就會變成2.625bit。霍夫曼編碼就是利用了這種大概率事件分配短碼的思想,并且證明這種編碼方式是最優(yōu)的。
從香農(nóng)給出的數(shù)學(xué)公式可以看出,信息熵其實(shí)是一個隨機(jī)變量信息量的數(shù)學(xué)期望。
前面給出了條件自信息量的定義,同樣可以得出條件熵的定義:
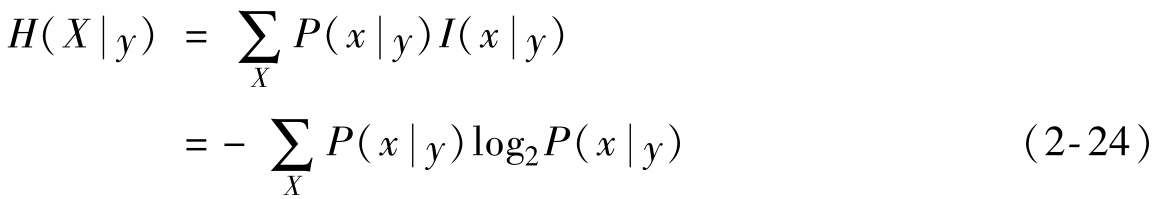
擴(kuò)展到整個Y集合,可以得到:
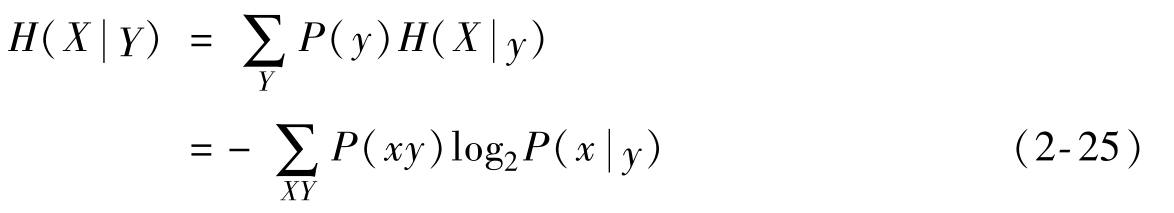
定義如下:對于聯(lián)合符號集X|Y,在給定Y的條件下,用聯(lián)合概率P(xy)對X集合的條件自信息量進(jìn)行加權(quán)的統(tǒng)計平均值,稱為X的條件熵。因此條件熵可以看作是信道給出的平均信息量。
【例2-3】已知X,Y∈{0,1},X、Y構(gòu)成的聯(lián)合概率為:P(00)=P(11)=1/8,P(01)=P(10)=3/8,計算條件熵 。
。
【解】由 ,可以得到
,可以得到
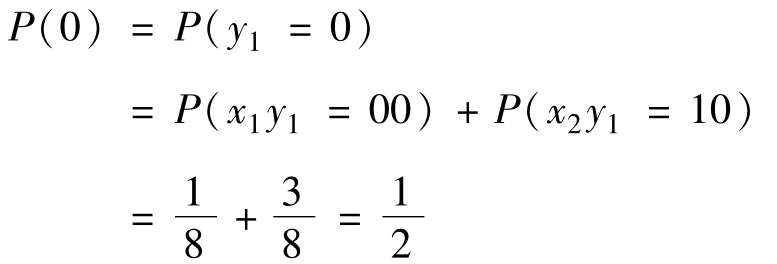
同理,可以得到
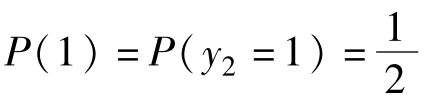
由 ,i,j∈{1,2},可以求得
,i,j∈{1,2},可以求得
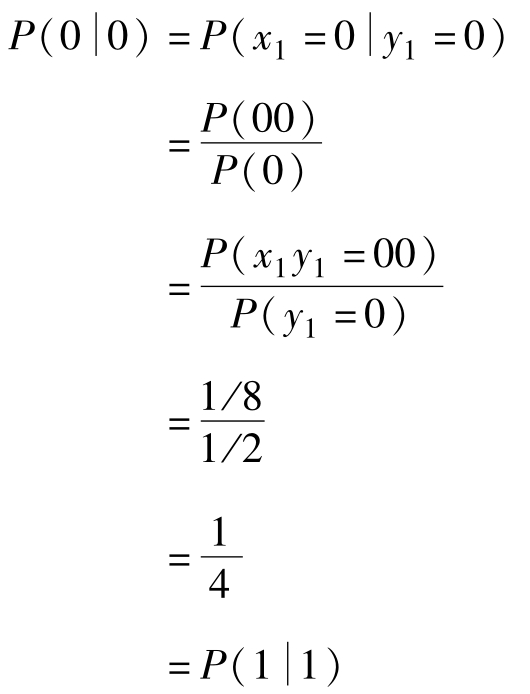
同理, ,可以求得
,可以求得
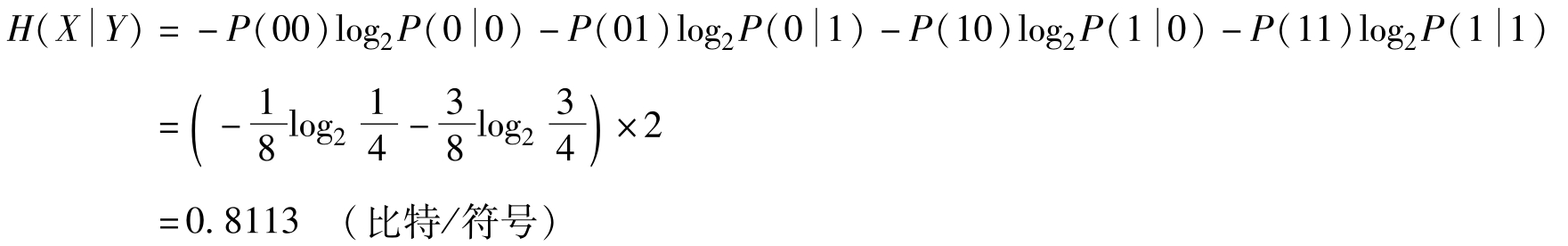
- 上海財經(jīng)大學(xué)統(tǒng)計與管理學(xué)院432統(tǒng)計學(xué)[專業(yè)碩士]歷年考研真題(含復(fù)試)匯編
- 3D服裝設(shè)計與應(yīng)用
- 服裝CAD應(yīng)用技術(shù)
- 保險學(xué)
- 跨境電子商務(wù)理論與實(shí)務(wù)
- 希爾《國際商務(wù)》(第11版)課后習(xí)題詳解
- 李廉錕《結(jié)構(gòu)力學(xué)》(第5版)(上冊)配套題庫【名校考研真題+課后習(xí)題+章節(jié)題庫+模擬試題】
- 電視照明(第三版)
- 消費(fèi)者行為學(xué)(第3版)
- 組織行為學(xué)(第3版)
- 設(shè)計美學(xué)
- 市場調(diào)查與預(yù)測教程
- 紅外熱成像檢測及其應(yīng)用
- 工程導(dǎo)論
- 設(shè)計構(gòu)成