2.1 信源數學模型
任何信源產生的消息輸出都是隨機的,可以用隨機變量、隨機向量或者隨機過程來描述,也可以用概率空間來描述信源。信源的輸出常常以符號或者代碼的形式出現,比如文字、符號、字母等,取值范圍是有限或者可數的。例如,投硬幣,每次不是正面就是反面;投骰子,每次都是1~6點中的一個,結果是隨機的,并且一定是集合中的某一個。因此,這樣在時間和幅度上離散分布的信源稱為離散信源,數學模型為離散型的概率空間,下面以一維離散隨機變量X來描述信源輸出
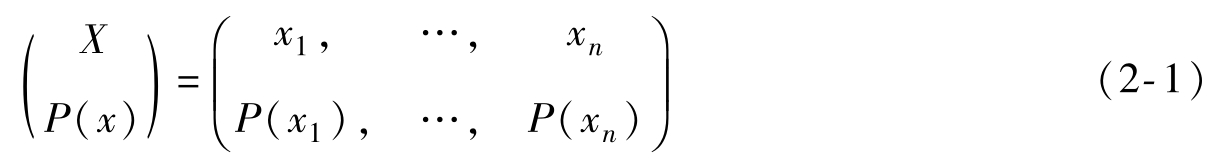
式中,P(xi)(i=1,…,n)滿足

其中,P(xi)(i=1,…,n)表示隨機事件X發生某一結果xi的先驗概率,該公式表示信源的可能取值范圍是有限的,共有n個,每次輸出必定為其中某一個。這是離散信源中最為基本的一種。
還有一種類型的信源,其取值在時間和幅度上都是連續分布的,同時又是隨機的,例如語音信號、圖像、電流值和電壓值等。這種信源稱為連續信源,其數學模型為連續型概率空間:

并且

其中,p(x)表示隨機變量X的概率密度函數。
離散信源和連續信源屬于最基本的兩種信源。下面簡單歸納幾種常見的信源類型。
離散平穩信源:若信源輸出的N維隨機序列X中,每個隨機變量Xi(i=1,2,…,N)都是取值離散的離散型隨機變量,并且Xi的概率分布都與時間起點無關,即在任意兩個不同時刻x和y(x和y為大于1的任意整數),對于任意的N=0,1,2,…,XxXx+1…Xx+N和XyXy+1…Xy+N具有相同的概率分布。這種各維聯合概率分布均與時間起點無關的信源稱為離散平穩信源。
連續平穩信源:若信源輸出的N維隨機序列X中,每個隨機變量Xi(i=1,2,…,N)都是取值連續的連續型隨機變量,并且Xi的概率分布都與時間起點無關,即在任意兩個不同時刻x和y(x和y為大于1的任意整數),對于任意的N=0,1,2,…,XxXx+1…Xx+N和XyXy+1…Xy+N具有相同的概率分布。這種信源稱為連續平穩信源。
離散平穩信源分為有記憶和無記憶兩種類型。
(1)離散有記憶信源
一般情況下,信源先后發出的符號之間是互相關聯的,也就是說信源輸出的平穩離散隨機序列X中,各隨機變量之間是有依賴的,例如,在中文字母組成的中文消息中,前后文字之間是有關聯的,稱這種信源為離散有記憶信源。故在N維隨機向量的聯合概率分布中,引入條件概率分布來描述它們之間的關聯。
(2)離散無記憶信源
離散無記憶信源是最簡單的離散信源,可以用完備的離散型概率空間來描述,其主要特點是離散和無記憶。離散指的是信源可能輸出的消息的種類是有限的或者是可數的,消息的樣本空間R是一個離散集合。由于信源的每一次輸出都是按照消息發生的概率輸出R中的一種消息,因此信源輸出的消息可以用離散隨機變量X表示。無記憶是指不同的信源輸出消息之間相互獨立。
連續平穩信源也可以分為有記憶和無記憶兩種類型。
(1)連續平穩無記憶信源
在連續平穩信源情況下,若信源輸出的連續型隨機向量X=(X1X2…XN)中,各隨機變量Xi之間無相互依賴、統計獨立,其聯合概率密度函數滿足
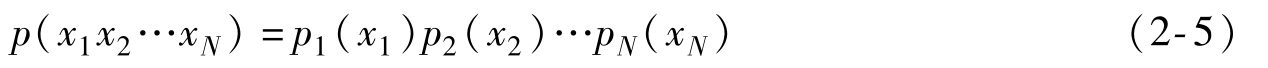
因為信源是平穩信源,因此p1(x)=p2(x)=…=pN(x)=p(x),那么p(x1x2…xN)= ,該信源稱為連續平穩無記憶信源。
,該信源稱為連續平穩無記憶信源。
(2)連續平穩有記憶信源
有依賴關系的連續平穩信源為連續平穩有記憶信源。