2.2　晶體宏觀物理性質與晶體對稱性

晶體的宏觀物理性質是指晶體對外界施加的各種作用的響應,它由宏觀可測物理量之間的關系定義。晶體的宏觀物理性質用張量描述,它受到兩種完全不同的對稱性的影響,一是晶體本身對稱性(晶體所屬點群)對宏觀物理性質的影響;二是熱力學關系(守恒定律)賦予物理性質本身的固有對稱性對宏觀物理性質的影響(見2.3節)。

2.2.1　晶體的宏觀物理性質

描述物質宏觀物理性質的物理量由宏觀的可測量的物理量之間的關系定義。例如物質的密度ρ是由質量m和體積V之間的關系m=ρV來定義的。又如電極化率χ則由施加于材料上的電場強度E和由此感生的電極化強度P之間的關系P=ε0χE來定義。其中m、V、P、E等都是可測物理量。

一般而言,若可測物理量之間的關系為線性時,則可采用如:

B=CA(2?7)

這樣的公式來表示,其中A稱為作用物理量,代表所施于材料的各種類型的作用,B稱為感生物理量或效果物理量,是在該材料中對A的響應而產生的物理量。A和B只描述對材料施加作用及由此所產生的響應,都是可測的量,但它們并不表示材料本身所具有的任何性質,故一般稱為場量,C代表A和B之間的關系,不同材料雖然受到相同的A的作用,但會得到不同的效果量B,這是由于不同材料具有不同的C值而造成的。因此,C代表了材料本身所具有的特性,即材料的物理性質,稱為物質量。通常,C是用物質系數來表示,例如電極化率、介電系數等。

2.2.2　用張量描述宏觀物理性質

(1)場量和物質量都是張量

有些物質量(如質量、體積、密度等),其數值與測量的方向無關,這樣的量沒有方向性,稱為各向同性量,也稱為標量。由于材料密度不均勻,密度可能會在不同點有不同的數值,即密度為點坐標(x1,x2,x3)的函數,但各點的數值仍然是與方向無關的。有些量(如電場強度E、電極化強度P),其值不僅有一定大小,而且還具有一定的方向性,這些物理量在直角坐標系中可用三個分量數值的大小來表示其方向性,這類量稱為矢量。除了矢量外,還有些物理量,如作用于材料上的應力和由之感生的應變,它們既具有一定量值,又具有一定的方向性,在直角坐標系中,它們已不能只由三個分量而必須由九個分量的組合才能描述,每個分量具有兩個下標,這樣的物理量稱為二階張量,如應力可以寫成:

σ=(2?8)

同樣,晶體的電極化率χ也是一個二階張量,由于晶體的各向異性,在某點的電極化強度P并不與該點的電場強度E有相同的方向,如圖2?5所示。

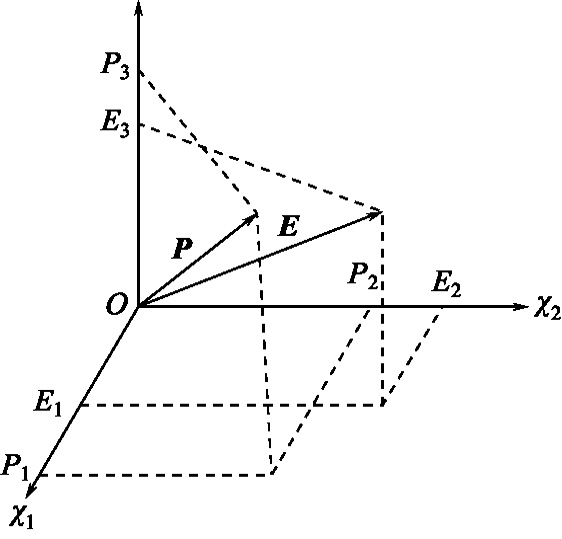
圖2?5　晶體中的P和E

那么電場強度和電極化強度之間的關系為:

(2?9)

若用矩陣表示,則可寫成:

=(2?10)

因此有:

χ=(2?11)

通常,一個三維空間的張量是3n個數的有序集合的總稱,n稱為該張量的階數。

(2)用張量描述晶體的物理性質

根據公式(2?7),材料的物理性質用物質量C表示,由上面討論可知,無論場量還是物質量都是張量,因此在一般情況下,材料的物理性質顯然可用張量來描述。考慮到場量A和B可以是階數不同的張量,所以用張量形式來表示式(2?7)時可寫成下式:

Bijk…=Cijk…lmn…Almn…(2?12)

式中,Almn…為p階作用張量;Bijk…為q階感生張量;根據張量的運算法則,Cijk…lmn…為p+q階物理性質張量。

從公式(2?12)中可以看出,我們必須使用張量來描述材料的物理性質,因為張量既能反映該性質的數量特征,也可以表示出其方向特征。晶體具有各向異性,與各向同性的材料相比較,晶體的相當數量的物理性質與方向就更為明顯。

2.2.3　晶體對稱性對晶體宏觀物理性質的影響

晶體的宏觀對稱性和晶體的宏觀物理性質都是晶體的內部長程有序在宏觀性質上的反映,因此,晶體的宏觀對稱性必對其物理性質產生影響。設沿晶體某一個方向測定其物理性質,使晶體做一次點對稱操作,固定在晶體上的坐標系必然經歷旋轉、反映等到新的坐標系,新舊坐標系之間由正交變換聯系。由于對晶體進行的是對稱操作,測得的物理性質不應該改變,即對晶體進行點群操作不會使晶體宏觀可測物理性質產生任何可以測量的變化。正是根據這種理解,并研究了大量實驗現象之后,得到了晶體宏觀物理性質和晶體對稱性的兩條基本原理。

(1)諾埃曼(Neumann)原理

諾埃曼(Neumann)原理是指晶體的任一物理性質所擁有的對稱要素,必須包含晶體所屬點群的全部對稱要素。

諾埃曼原理是指晶體物理性質的對稱性必然高于或至少不低于晶體所屬點群的對稱性,但它并未斷言,晶體物理性質的對稱要素一定與晶體所屬晶類的對稱要素相同。居里原理是指當外場的對稱性高于晶體對稱性時,晶體的對稱性保持不變;而當外場的對稱性低于晶體的對稱性時,外場作用后晶體的對稱性要降低。

從諾埃曼原則與居里原理出發,可以推導晶體物理性質的對稱性與晶體宏觀對稱性之間的三條規律:

① 凡是具有中心對稱的晶體,都不可能具有用奇數張量描述的物理性質;

② 一切晶體都具有偶數階張量描述的物理性質;

③ 只有極性晶類才具有一階張量描述的物理性質。所謂極性晶類是指晶體中的單向與極軸相一致的晶類,這里單向是指晶體中的特殊方向,即晶體中不能通過本身所具有的對稱要素的作用而與其他方向重復的方向。

(2)居里原理

居里原理是指晶體在受到外場作用后,晶體的對稱要素僅保留晶體原有對稱要素中與外場的對稱要素相一致的那一部分。

當晶體受到外場作用,但這種作用對晶體結構和晶體對稱性的影響可以忽略的情況下,諾埃曼原理是完全正確的。在一般情況下,外場的這種作用常常可以忽略,但對某些敏感的物理性質,外場的影響就比較明顯,因此不能忽略。例如,在外電場或外應力場的作用下,立方晶體的光學性質將發生變化,由原來的光學各向同性變成類似于單軸晶或雙軸晶性質。如果把諾埃曼原理看作是外場作用前晶體對稱性與晶體物理性質間的相互關系的準則,那么居里原理可以看成是外場作用后確定晶體對稱性的準則。外場作用后,晶體對稱性與晶體物理性質間的關系仍然滿足諾埃曼原理。