- 優化驅動的設計方法
- 高亮 邱浩波 肖蜜 李好
- 2317字
- 2021-12-10 16:41:16
2.6 數值算例
本部分將通過二維和三維結構設計實例來說明所提出方法的特點。如前述假設,CSRBF的節點與有限元網格節點坐標一致,尺度因子dmax取值為4。人工材料模型中的實體部分彈性模量為180GPa,孔洞部分彈性模量為0.18GPa,泊松比為0.3。優化問題的算法終止條件為相鄰兩次迭代目標函數的相對容差小于1E-4。所有實例均采用MATLAB編程,且在CPU主頻2.6GHz、內存8GB的計算機上運行。
2.6.1 二維懸臂梁結構剛度拓撲優化設計
圖2-5給出了某二維懸臂結構的設計空間,結構設計域的長寬比為2∶1。結構左端約束其全部自由度,右端的中點處施加大小為10kN的向下集中載荷。這里的優化目標設置為結構柔度最小化,設計約束為材料的體積分數不超過50%。
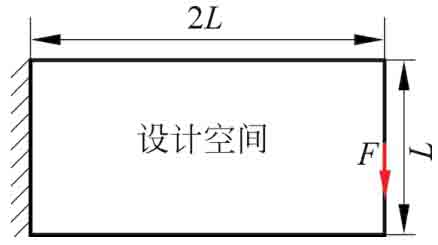
圖2-5 二維懸臂梁結構的設計空間
首先將二維懸臂梁的設計域離散為80×40個四節點有限單元,于是CSRBF插值矩陣中將含有(81×41)2=11 029 041個元素。利用DWT技術對CSRBF插值矩陣進行壓縮的關鍵是選定合適的閾值調整參數κ,見式(2-28)。首先令κ=20,以觀測參數化水平集方法優化效果。
閾值調整參數κ=20時的結構優化過程如圖2-6所示,所對應的高一維水平集函數變化如圖2-7所示。觀察優化過程可以發現,參數化水平集方法很好地保留了傳統水平集方法在精確捕捉結構拓撲和邊界形狀方面的優勢。此外,最優結構拓撲也表現出了光滑的結構邊界和清晰的材料界面。目標函數和體積約束的收斂曲線如圖2-8所示,算法在第259次迭代時收斂,最優拓撲所對應的結構柔度值為86.2716。值得注意的是,在前幾步迭代中,目標函數值并沒有下降。這是因為本例給出的初始設計違反了體積約束,在優化迭代的初始階段,算法要迅速刪除材料以滿足設定的體積約束。在約20次迭代后,結構的最優拓撲已經形成,隨后的迭代主要是對結構邊界的形狀進行優化,從而使結構的柔度達到最小。從整個收斂曲線圖來看,目標函數值穩定降低,結構體積約束得到滿足,說明了方法的有效性[16]。
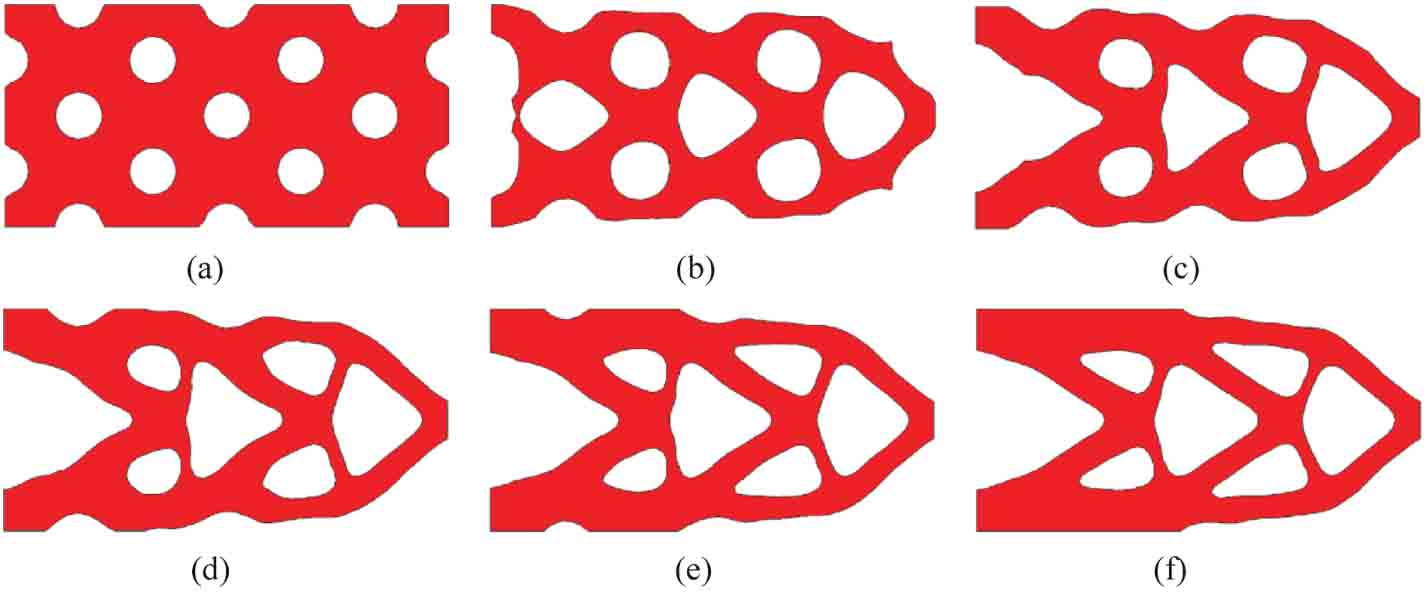
圖2-6 二維懸臂梁結構的優化過程
(a)初始設計;(b)第10次迭代;(c)第20次迭代;(d)第40次迭代;(e)第100次迭代;(f)最終設計
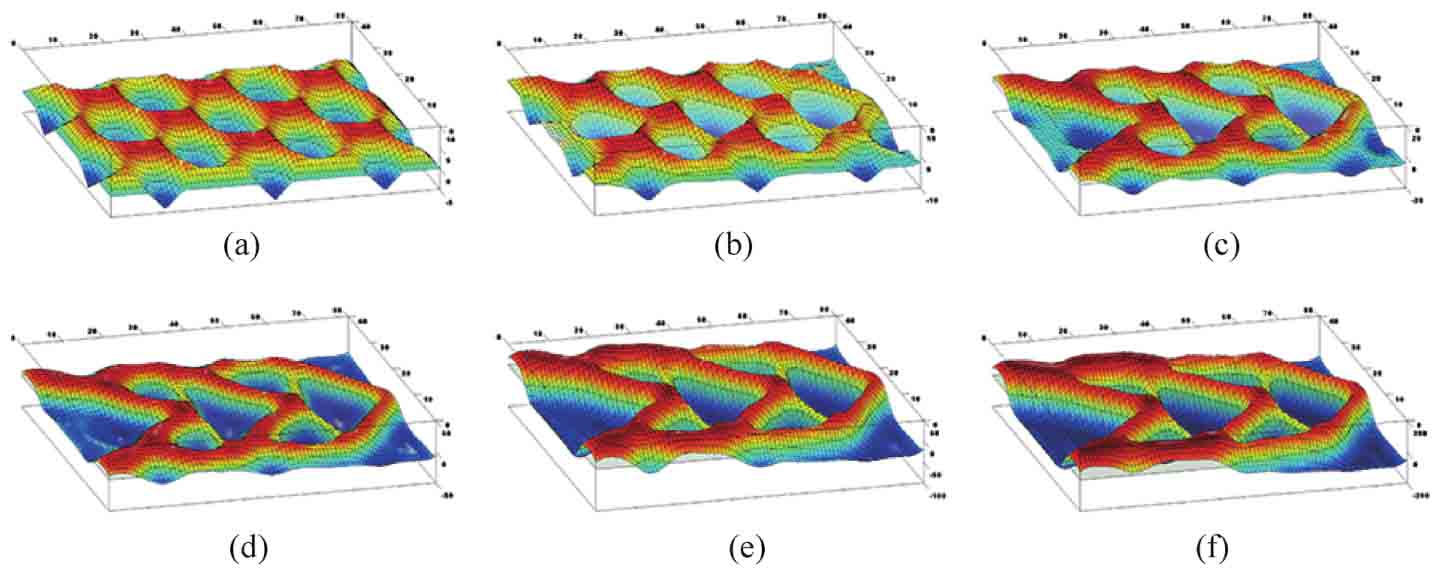
圖2-7 二維懸臂梁結構對應的水平集面演化過程
(a)初始設計;(b)第10次迭代;(c)第20次迭代;(d)第40次迭代;(e)第100次迭代;(f)最終設計
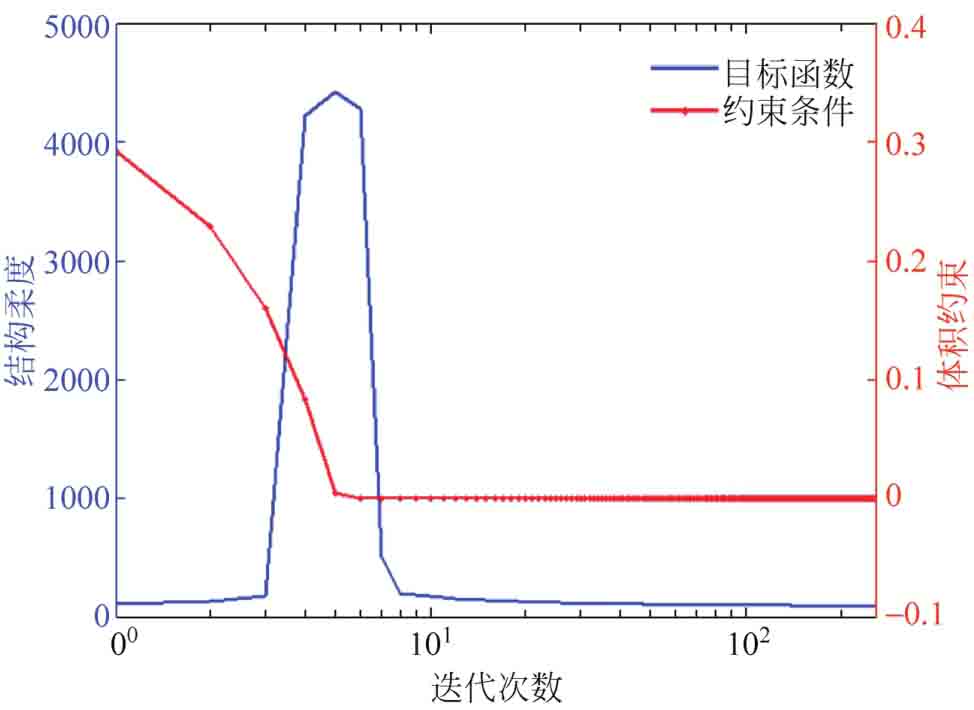
圖2-8 目標函數與約束條件的迭代收斂曲線
1)閾值參數的影響
在所敘述的參數化水平集方法中,閾值參數κ有重要影響,將決定方法的精度和效率。本部分采用6個例子進行對比分析:前2個例子分別采用GSRBF和CSRBF插值方法,后4個例子采用CSRBF和DWT相結合的插值方法,并設置不同的閾值參數值。所有例子均采用相同的初始設計,設計域均離散為80×40個有限單元。
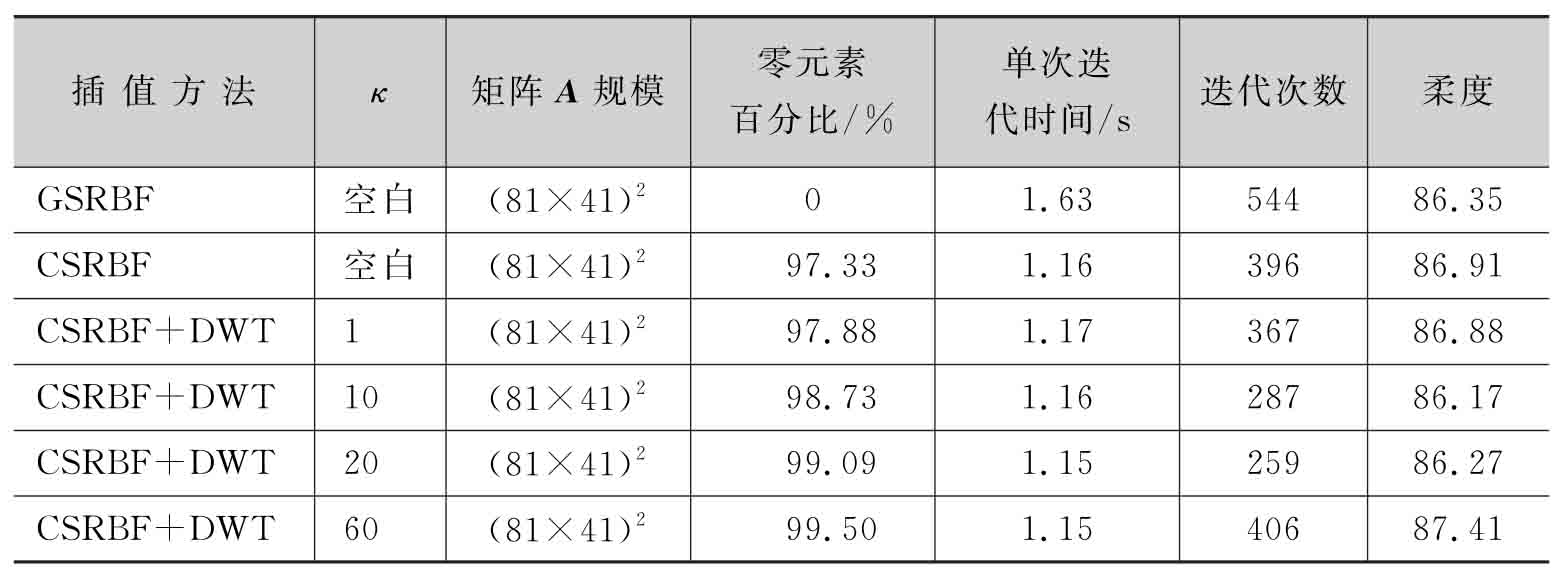
圖2-9和表2-1給出了6組不同例子的優化結果。通過優化結果不難發現,利用CSRBF和DWT相結合的插值方式,閾值參數越大,插值系統稀疏度越高,計算效率越高,但過大的閾值參數可能會導致插值精度顯著下降,表現為結構邊界不光滑和迭代次數增加。反之,較小的閾值參數(如κ=1,10)計算效率較低,但插值精度更高。通過設置合適的閾值參數(例如κ=20),所提出方法的插值矩陣中零元素達到99%以上,相較于GSRBF直接插值的方式能夠顯著提升優化效率;相較于CSRBF直接插值方式,在插值系統的稀疏度、求解時間、迭代次數以及最優目標值方面均較優[16]。
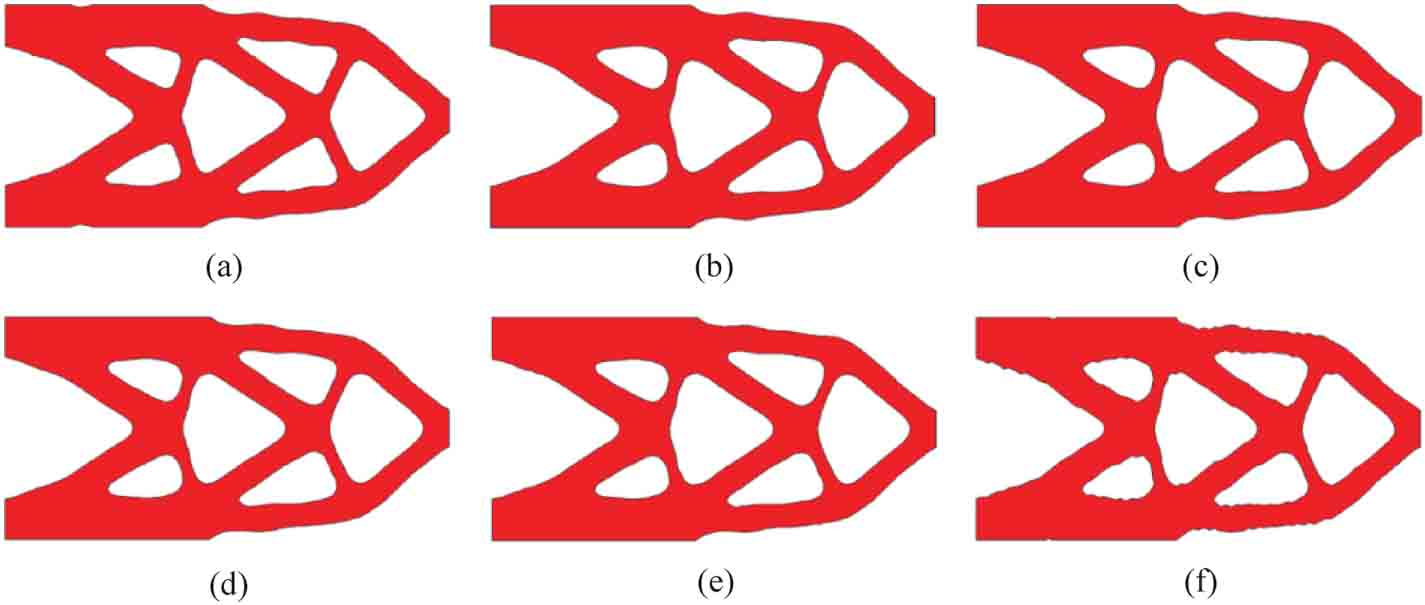
圖2-9 6組不同例子的最優結構拓撲
(a)GSRBF;(b)CSRBF;(c)CSRBF+DWT,κ=1;(d)CSRBF+DWT,κ=10;(e)CSRBF+DWT,κ=20;(f)CSRBF+DWT,κ=60
表2-1 插值方法和閾值參數的影響
2)有限元網格規模的影響
本部分對圖2-5所示的設計空間分別采用80×40、120×60和160×803種規模的有限元網格進行離散,從而來討論有限元網格對優化效果的影響。所有例子中,閾值參數均設置為κ=20,結構的初始設計如圖2-6(a)所示。
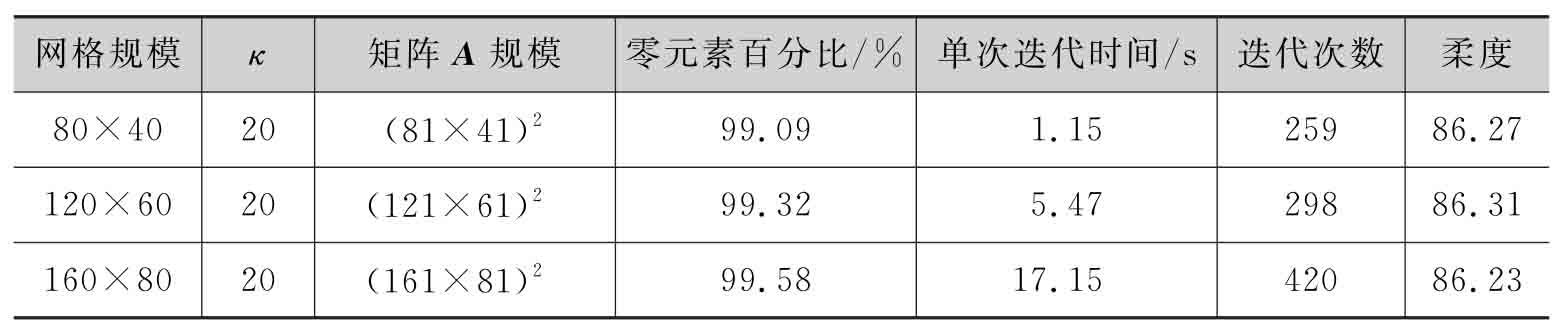
不同網格規模對應的優化設計結果如圖2-10和表2-2所示。隨著有限元單元數量的增加,優化計算的成本也迅速增加。然而采用本章所論述的參數化水平集方法總能獲得極其稀疏的插值矩陣,意味著更新水平集函數所需的時間及計算機內存將極大減少。3個例子的最優結構拓撲展現出清晰、光滑的邊界,說明盡管該方法僅利用較少的非零元素進行插值,但其精度完全能夠滿足工程需求。不同網格規模下的最優結構拓撲及其對應的柔度值相差無幾,說明本章所論述的參數化水平集方法可以有效避免網格依賴性。其原因在于CSRBF插值中緊支域半徑是一個重要參數,它決定了最優結構拓撲的復雜程度,若在優化時采用相同的緊支域半徑,不同粒度的有限元網格下的優化設計便能收斂到相似的拓撲形式[16]。
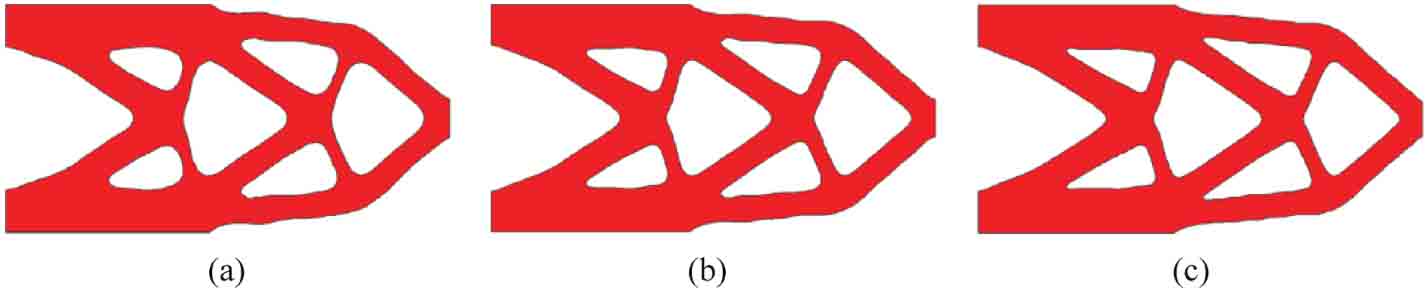
圖2-10 采用不同有限元網格規模時的最優結構拓撲
(a)網格規模80×40;(b)網格規模120×60;(c)網格規模160×80
表2-2 不同有限元網格的影響
2.6.2 三維懸臂結構剛度拓撲優化設計案例
三維懸臂結構的設計空間如圖2-11所示,結構的左端約束全部自由度,右端作用300kN向下的集中載荷。本例的設計域采用20×8×40個八節點有限單元進行離散,由于結構設計域及其邊界條件關于y軸對稱,因此有限元模型可以簡化為20×4×40個。本例的優化目標為結構柔度最小化,設計約束為結構體積分數不超過50%。
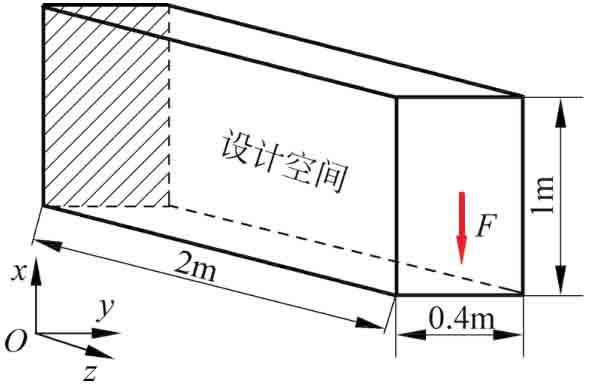
圖2-11 三維懸臂結構的設計空間
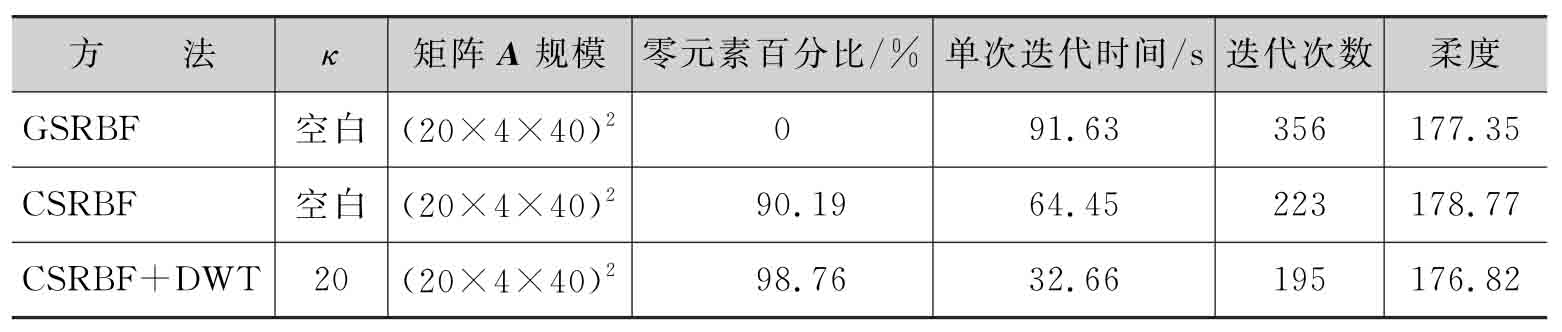
分別采用3種方法對本例所涉及的優化問題進行求解,即①CSRBF+DWT且閥值參數κ=20;②CSRBF直接插值法;③GSRBF直接插值法。采用插值方法①時的三維懸臂結構的初始設計和最優設計如圖2-12所示。算法經過195次迭代達到收斂,結構柔度從最大時的385.45下降至176.82,結構體積分數為50%,完全滿足約束條件,最優設計亦顯示出光滑、清晰的結構邊界。分別由3種插值方式構建的參數化水平集拓撲優化方法所對應的優化結果如表2-3所示。可以明顯看出,針對規模更大且更加復雜的三維結構拓撲優化問題,在保證計算精度的前提下,CSRBF+DWT方法優化效率遠高于GSRBF和CSRBF方法,驗證了本方法的優越性。
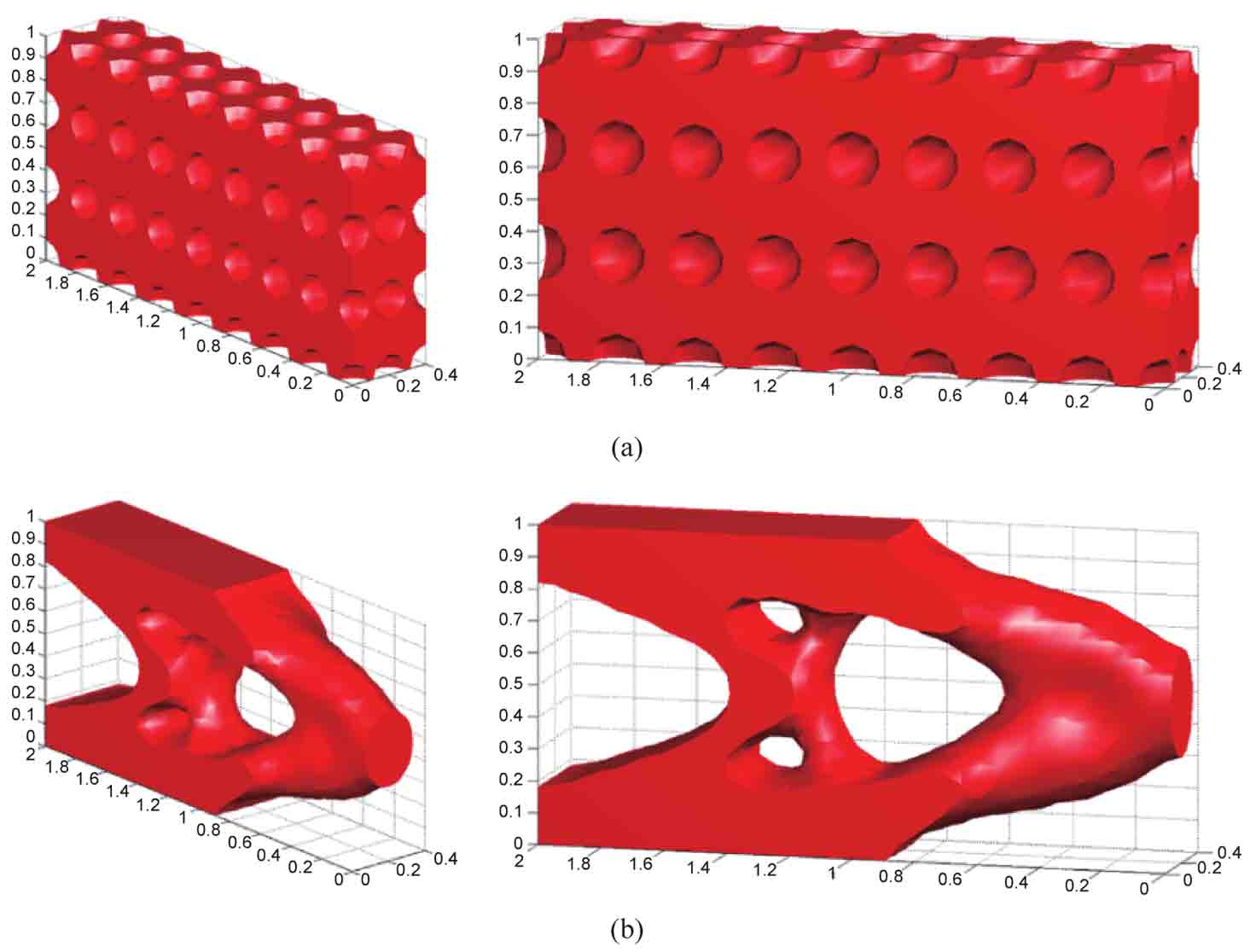
圖2-12 三維懸臂結構的初始設計與最優設計
(a)初始設計;(b)最優設計
表2-3 不同插值方式在三維結構拓撲優化問題中的對比
- C語言程序設計案例教程
- Learning Java Functional Programming
- Apache Oozie Essentials
- 造個小程序:與微信一起干件正經事兒
- Mastering Objectoriented Python
- Visual C++數字圖像模式識別技術詳解
- Java性能權威指南(第2版)
- Microsoft System Center Orchestrator 2012 R2 Essentials
- SQL經典實例(第2版)
- C語言程序設計
- Mastering Backbone.js
- MongoDB Cookbook(Second Edition)
- 原型設計:打造成功產品的實用方法及實踐
- Laravel Design Patterns and Best Practices
- C語言程序設計教程