- 商業銀行零售客戶資產配置行為研究
- 咬亮
- 3694字
- 2020-04-10 12:02:42
2.2.3 損失厭惡資產配置理論的相關研究
(1)損失厭惡與風險厭惡的關系
在經典的M-V模型中,風險厭惡系數往往被認定為一個常值。但行為金融理論認為,將風險厭惡系數設定為常數不符合現實,Brauers(2008)等認為投資者的風險厭惡系數會隨著其收益、財富水平的變化而變化。損失厭惡在現實經濟中的表現有:貨幣幻覺、稟賦效應、終局效應、股票溢價之謎、過度自信等。同樣,損失厭惡系數成為衡量不同投資者對同一筆金額損失的厭惡程度,多是基于調查問卷評價而來,既有主觀成分又有經驗依據。
風險厭惡(Risk Aversion)。對于投資者而言,放棄公平的賭局和更差的投資,而愿意考慮無風險資產和有正風險溢價的投資,會“處罰”除去風險組合一定的收益率,以彌補其承擔的風險,即風險越大,處罰越大,這就是對風險厭惡的描述性定義。雖然對于投資而言,是承擔一定的投資風險并獲取相應的報酬,但對“一定的風險”和“相應的報酬”卻很難準確定義。可以說,“一定的風險”是說風險水平足夠影響投資決策,一個投資者也許會因為一項投資產品的潛在收益并不足以彌補它的風險而放棄投資,“相應的報酬”是指投資有正的風險溢價,即期望收益高于無風險收益率。從目前來看,大量深入的研究表明(Roy,1952;Simaan,1997;徐緒松等,2002),絕大多數投資者是風險厭惡的,只是風險厭惡的程度不同,對于一個極度風險厭惡的投資者而言,任何風險組合甚至風險溢價為正的投資,其效用都有可能低于無風險資產,于是其拒絕風險資產組合;相反,風險厭惡程度較低的投資者可能從同樣的風險資產組合獲得的效用高于無風險資產從而愿意投資。當然,與風險厭惡相對,風險偏好的投資者更愿意參加公平博弈或其他賭博,風險中性的投資者不需要風險補償。一般而言,風險厭惡程度就是用來衡量投資者對風險的態度,而這也主要借助調查問卷獲取。
損失厭惡(Loss Aversion)。行為金融學理論認為,投資者對待風險的態度是損失厭惡而非風險厭惡型,這在Tversky和Kahneman的描述性定義中可以看出,投資者在面臨同筆金額的收益或損失時,損失帶給其的負效用遠大于收益帶來的正效用。這個心理學在投資領域的發現,有力地解釋了諸多“金融異象”,也得到了廣泛的認可和應用。如果讓投資者在A.100%獲得1000元和B.70%概率2000元之間選擇時,實驗對象大多選擇了A,同樣,如果再讓同一批投資者在A.100%損失1000元和B.70%概率損失2000元之間選擇時,實驗對象卻又選擇了B。前景理論(Prospect Theory)的創始人特維斯基和卡爾曼(Tversky & Kahneman,1979)指出,如有實驗對象是風險厭惡的,兩種情況下都會選擇A,同樣,如果實驗對象是風險偏好的,兩種情況下都會選擇B,那么,這將違背偏好假定中的一致性公理。上述實驗現象從理論上說明,傳統經濟學將風險厭惡設定為外生的,而行為金融學卻認為是內生的,投資者可以同時具備冒險和保守兩種投資心理。
(2)損失厭惡模型的參數設定
在Kahneman和Tversky(1979)的S型前景價值函數中,最為重要的參數有3個(α,β和λ),α和β是解釋效用對獲利和損失敏感性的曲率參數,λ是度量損失厭惡程度的系數,它們共同刻畫投資者對損失的態度或程度,并通過實驗得出α和β取值0.88,取值越大說明越愿意冒險,λ取值2.25。
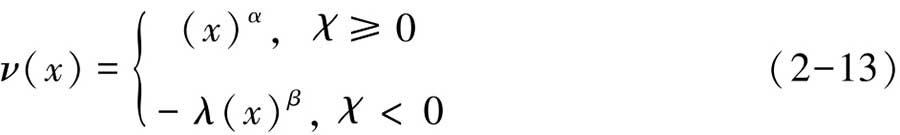
此后的研究者也多用此作實證研究,如Benartzi和Thaler(1995),Berkelaar(2004)等,Barberis和Huang(2001),Camerer和Ho(1994)與Wu和Gonzalez(1996)認為盡管α,β取值一樣,但較Thaler等(1995)的估計要小;同樣,Patricia(2009)通過非線性回歸方法研究損失厭惡對貿易政策的影響時,發現λ大約為2;Booij等(2010)在研究效用函數和概率權重函數時,發現λ約為1.6;Hwang和Satchell(2010)發現λ在不同國家或地區的市場上會有所差異,英、美市場的λ分別為3.25和2.75。
Abdellaoui M.等(2007)認為當前對損失厭惡參數的研究實驗很多,但學術界還未有統一定論。Schmidt等(2002)研究了動態的損失厭惡情形,提出了絕對和相對的損失厭惡溢價。Brooks等(2005)通過學生實驗得出被試者整體都有顯著的損失厭惡。自Thaler將損失厭惡引入非風險領域后,Novemsky等(2005)用商品買者愿意支付的最高價與賣者愿意支付的最低價差距來衡量損失厭惡程度,但還未將研究擴展到風險領域。Gachter(2007)等通過“稟賦效應”實驗發現,風險狀態不同,損失厭惡程度也不同,且無風險決策與風險決策的損失厭惡有顯著的正相關。除此之外,收入、財富、年齡會加重損失厭惡程度,而學歷會減輕損失厭惡程度。Abdellaoui(2007)等通過實驗得出了效用函數圖形,進而得到損失厭惡系數。Thaler和Johnson (1990)在發現“私房錢效應”時,Gervais和Odean(2001)提出“過度自信”假說時,都曾預測“牛市”行情會降低投資者的損失厭惡程度,進而導致投資行為更加激進;Berberis等(2001)認為市場處于“熊市”時,投資者對損失和風險的厭惡程度將上升;李雪峰(2011)等的研究證明了在“牛市”行情中,投資者因普遍盈利而高估了自身的投資能力,致使損失厭惡程度降低;肖峻(2013)認為投資者“處置效應”強弱會受到“私房錢效應”和“過度自信”的影響,因為正是認知偏差導致損失厭惡程度和風險厭惡程度的不同,最終導致投資者行為呈現出不對稱性。
除此之外,Kahneman和Tversky(1979)將收益和損失的參考點(Reference Point)設定為0,這在后來的研究者看來并不完善,這取決于投資者的心理認定和因環境變化而變化。研究者們只關注單一參照點,但不久之后便意識到多種參照點會同時作用于決策過程(Huang & Tseng,2007;Koop & Johnson,2012)。當前,國內外學者主流應用的是由Wang(2002),Wang和Johnson (2012)提出的三參照點理論(Tri-reference Point Theory),認為在風險決策時,行為主體考慮了最低要求(Minimum Requirement,MR)、現狀(Status Quo,SQ)和目標(Goal,G)三個參照點,并將心理預期劃分為四個區域(Area):成功(D> G)、收益(SQ<C<G)、損失(MR<B<SQ)和失敗(A<MR),投資者避免失敗是最重要的,其次是成功,最后是維持現狀,這也為損失厭惡提供了新解釋,投資者從損失到失敗的心理效應要遠大于從獲益到成功,又被稱為失敗厭惡(Failure Aversion);王曉田和王鵬(2013)認為在動態決策中,MR和SQ影響投資者的風險傾向,而G則在最后一輪的投資中發揮作用。
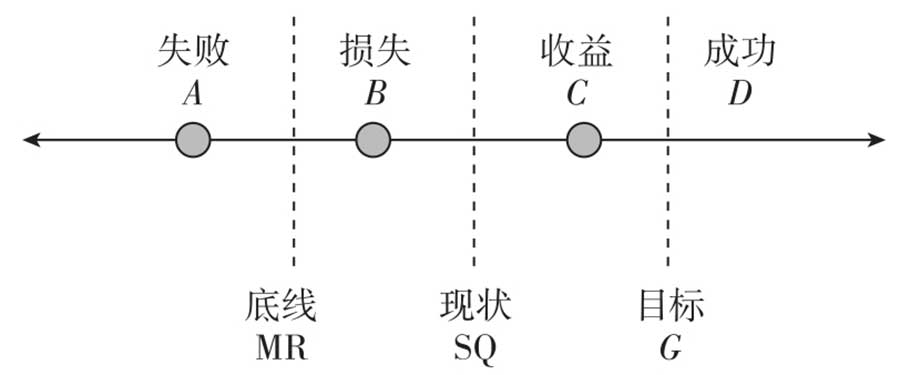
圖2-2 三參照點理論圖示
從中可以看出,研究者分析因素各有不同,對于前景價值函數的參數取值也各有不同,但對分析資產配置行為研究卻至關重要,既往有Wakker和Deneffe(1996)的權衡法(Trade-off)、Abdellaoui等(2007)的無假設測度法,而國內學者在損失厭惡參數測度方面的研究極少。
(3)損失厭惡資產配置模型的相關研究
Markowitz的均值方差模型是資產配置的經典分析范式,影響深遠,但其關于理性經濟人、有效市場假說等研究較現實有所偏差,故從有限理性出發的行為金融學成為資產配置的新理論工具。衛海英(2002)認為均值—方差的傳統風險測量方法放大了大方差的風險卻縮小了小方差的風險,而且忽視了小方差風險的累計作用,這是M-V理論的缺失;李臘生(2013)認為將投資者假定為同質預期、風險偏好一致是不符合現實的。因此,資產配置理論的研究方法就集中在如何測度投資者的風險上,出現了下半方差、下側風險和在險價值等有別于傳統均值—方差的風險測度方法,如Foo等(2000),Estrada等(2008)以半方差測度資產組合風險,Hallow(1989)提出了下偏矩方法(Low Partial Moments,LPM)。事實上,Rockafeller等(2000)認為VaR模型或CVaR模型也是基于下側風險或基于參照點損失的思路;汪貴浦等(2003)用非線性方法改良了Hallow模型,使其能夠求解一階下偏矩的精準值;Usman Ayub等(2005)將下偏二階矩的資產配置模型與均值—方差、均值—半方差模型進行了比較,并就模型的收益偏度、優化算法、穩健性檢驗等方面作了進一步研究;李仲飛(2010)對單期、多期資產配置問題進行了最優解,姚海洋等(2014)在不確定決策理論的框架下用傳統資產組合理論通過不斷修正假設條件的效用函數尋求最優解。
在Kahneman和Tversky(1979)前景理論的S型模型框架下,通過改變參照點、損失厭惡系數等方式不斷完善前景價值函數,Barberis等(2001)結合心理賬戶研究了線性前景理論函數(Linear Prospecet Theory Model,LPT),將α和β設置為1,而非Kahneman和Tversky的0.88,通過股票回報率和動態損失厭惡系數解釋了“私房錢效應”(Housing Money Effect);李仲飛、梅琳(2004)對CRRA、LA、DA三種效用模型進行了比較分析,認為DA(Disappointed Aversion)比LA更能解釋“金融異象”;Gomes等(2005)在此基礎上,通過改造的三段式LLA模型,發現投資者面對進一步的損失時會變得更加冒險,而獲利時又變得更為保守;De Giorgi E.等(2006)將其轉化為指數效用函數,胡支軍等(2010)通過優化算法,但都存在計算復雜、轉化后效果不佳的問題;Fortin等(2011)研究了MV、CVaR以及LLA達到相同最優解的條件,并對歐美股票市場進行了實證研究。
Cumova等(2014)拓展了前景理論,利用基于參照點的偏距測度收益或損失,并設定了上偏矩和下偏距(UPM-LPM),重點研究了對投資者風險和收益態度各異情況下資產組合及有效前沿問題;對于變量較多的非線性混合整數規劃問題,王純子等(2013)設計了一種擴展時間Petri網模型及其算法;林志炳(2010)、He(2011)、Fong(2013)和Best M.(2014)等假定損失厭惡函數為線性和投資者的邊際效用恒定來求最優解;王佳等(2016)考慮了資產均值的模糊不確定性以及投資者損失厭惡的心理,對風險資產收益分布未知條件下的分布魯棒投資組合問題;也有學者如詹澤雄、吳宗法等(2017)采用線性損失厭惡資產配置模型(Linear Loss Aversion Model,LLA)替代經典前景價值函數模型,來分析參照點動態變化和損失厭惡系數調整下的一組股票的最優配置比例,并將其與M-V在投資績效上作出對比,認為下偏二階矩的非線性損失厭惡資產配置模型具有更優的配置效率。