2.10 零空間

經(jīng)過線性變換后，被壓縮到原點的向量集合叫零空間。一個平面被線性變換壓縮成直線后，原平面中有一條直線的空間被壓縮到了原點，這條被壓縮到原點的直線就是零空間。

以圖2-18為例，假設(shè)存在一個矩陣，可以使標(biāo)準(zhǔn)平面直角坐標(biāo)系的兩個坐標(biāo)軸向一起靠攏，在較大夾角的開口處，向量會集體向兩側(cè)傾斜。但是正中間的“法線”不屬于任何一側(cè)，當(dāng)兩個坐標(biāo)軸合并在一起時，“法線”上的所有向量就會被集體“拽”到原點。這條直線上的向量空間就是零空間。

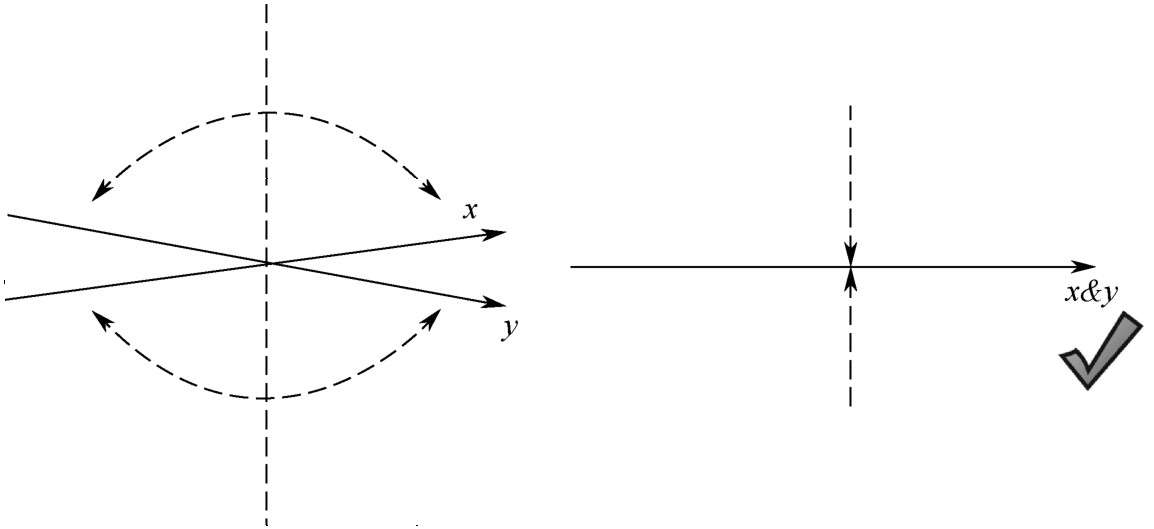
圖2-18 零空間

以公式來表達(dá)圖2-18，如下所示，所有可以被矩陣A變換壓縮到原點的向量x的集合，組成了零空間。

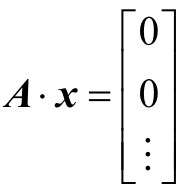
利用零空間的概念可以求解線性方程組。在上式中，如果向量x不在零空間內(nèi)，那么等式不成立，方程一定無解。反之，如果向量x能促成等式成立，那么就可能是方程的一個解。