1.2　國內外研究現狀

港口前沿的裝卸作業包括泊位分配、岸橋指派與岸橋作業調度3個方面。由于岸橋指派環節在現實作業中通常由調度人員根據經驗操作，且難度不大，因此該問題基本沒有引起學者們的重視。在現有文獻研究方面，也沒有專門針對岸橋指派的研究，因此，本節的文獻綜述就沒有涉及岸橋指派問題。

1.2.1　泊位分配

在現有文獻中，依據實際碼頭作業時泊位分布方式的不同，泊位分配主要分為離散型和連續型。前者是將碼頭前沿的岸線劃分為若干獨立的泊位進行分配，所劃分的泊位長度是固定的，來港船舶不能跨越泊位界限停靠，只能處于某個泊位所限定的位置空間內，這類問題可視為機器調度問題在港口裝卸領域的拓展；后者是指對于按直線布置的連續泊位，只要滿足到港船舶的物理條件就可以進行靠泊作業，也就是通常所說的柔性靠泊情況下的泊位分配，與離散型泊位問題不同的是，此時需要考慮到不同船舶的具體長度，而船舶可以停靠在碼頭的任意位置，不再有固定泊位的劃分，這類問題可視為切割問題在碼頭裝卸領域的拓展。顯然，連續型泊位分配要比離散型泊位分配能更好地利用有限的泊位資源，也更符合我國碼頭的實際情況。

依據船舶到達時間與泊位分配時間的先后，泊位調度還可以分為靜態和動態兩種。其中，靜態指在進行泊位分配時，所有需要靠泊作業的船舶均已到港，即不考慮后續船舶到達情形；而動態則指在泊位分配時，不但要考慮已在港的船舶，還要考慮同一計劃期內后續到港的船舶。簡而言之，在靜態情形下，可視為所有船舶的到港時間是相同的，均為時刻0；而在動態情形下，船舶是陸續到港的，因此到港時間是不相同的，可以不是時刻0。

Imai等（1997，2001）^[3]，[4]研究了離散泊位分配下的靜態與動態問題，以船舶在港時間最短（等待時間加裝卸時間）為目標構建了非線性整數規劃模型，并忽略FCFS（先到先服務）原則進行了分配作業，求解方面則采用了拉格朗日松弛法；Nishimura等（2001）^[5]在Imai等（2001）^[4]的研究基礎上，進一步考慮了船舶停靠的一些物理條件，如泊位水深和岸線長度，并采用遺傳算法進行求解。在碼頭作業中，管理者經常會根據自身戰略規劃，給到港船舶分配服務優先級，以保證高優先級別的船舶可獲得優先服務。船舶優先級別的標準是多種多樣的，有些港口會將裝卸作業量小的船舶定為高服務優先級，因為其裝卸作業時間短，整個港口船舶的等待時間會縮短；有些港口則將裝卸作業量大的船舶定為高服務優先級，因為其可以給港口帶來高額利潤。Imai等（2003）^[6]在Imai等（2001）^[4]的研究基礎上對不同服務優先級船舶的泊位合理分配問題進行了研究。Imai等（2007）^[7]以嵌入式泊位為研究對象，建立了泊位合理分配混合整數規劃模型。Hansen等（2008）^[8]研究了動態情形下的離散泊位分配問題，以最小化等待成本、裝卸成本與懲罰成本（提前作業與延遲作業）為目標構建了混合整數規劃模型，并采用變鄰域搜索法求解。Theofanis等（2007）^[9]研究了動態離散型泊位分配問題，提出的模型對Imai模型進行了改進，目標函數是使所有船舶的總在港時間最短，最后運用遺傳算法對提出的模型進行了求解。Imai等（2008）^[10]從動態和靜態的角度對問題進行分析研究，當船舶的服務時間超過它的截止時間后，船舶會被分配到外部碼頭繼續進行服務，最后采用遺傳算法對模型進行了求解。Cordeau等（2005）^[11]以最小化船舶等待時間與裝卸時間為目標建立了數學模型，并采用禁忌搜索算法求解。Buhrkal等（2011）^[12]分析了Imai等（2001）^[4]與Cordeau等（2005）^[11]的研究成果，對離散泊位分配問題構建了新的改進模型。Xu等（2012）^[13]考慮了水深與潮汐因素約束，分動態與靜態兩種情形研究了離散泊位分配問題，并分別設計了啟發式算法。Eduardo等（2012）^[14]研究了動態情形下的離散泊位分配問題，其優化目標是船舶等待時間與裝卸時間最短，并基于禁忌搜索算法設計了一種新的啟發式算法進行求解。張燕濤（2005）^[15]以所有在港船舶的總在港時間最短為目標，其目標函數是通過遞推的方式建立的，引入了在同一泊位上先后被服務的兩艘船舶服務時間之間的關系，即先服務船舶的離開時間與后服務船舶的到達時間之差。劉志雄（2010）^[16]建立的離散泊位分配問題考慮了先到先服務規則，采用了粒子群算法來解決問題。秦進等（2010）^[17]提出了考慮時間窗限制的離散型港口泊位分配的整數規劃模型，模型沒有考慮船舶靠泊的偏好位置。韓笑樂等（2009）^[18]考慮了船舶服務優先權，對動態情形下的離散泊位分配進行了研究，以最小化船舶總在港時間（指船舶等待時間）與加權延遲時間為目標建立了數學模型，并結合禁忌搜索與模擬退火算法設計了相應的啟發式算法。王紅湘等（2008）^[19]認為船舶裝卸時間取決于船舶所停靠的位置，構建了基于時間與成本的數學模型并進行了仿真研究。李平等（2006）^[20]將遺傳算法與禁忌搜索算法結合起來，設計了GATS混合優化算法進行求解。Golias等（2014）^[21]研究了船舶到港時間與裝卸作業時間均不確定情形下的離散泊位分配問題，以船舶平均在港時間與總服務時間變動最小為目標構建了雙目標混合整數規劃模型，該模型可生成帶有魯棒性的泊位分配方案，并設計了遺傳算法求解。Ting等（2014）^[22]以所有船舶等待時間與作業時間之和最短為目標構建了混合征稅規劃模型，并采用粒子群算法來求解。

在連續泊位分配方面，Li等（1998）^[23]將泊位分配—岸橋指派問題看作一個可同時處理多個任務的處理機調度問題，研究了靜態情形下的泊位分配問題，其中船舶裝卸時間被視為一個固定值。Lim（1998）^[24]證明了連續泊位分配問題屬于NP完全問題。類似地，Guan等（2002）^[25]也研究了靜態情形下的泊位分配問題，將泊位分配—岸橋指派問題看作處理機調度問題，其優化目標是最小化帶權重的任務完成時間。Wang等（2007）^[26]研究了動態情形下的泊位分配問題，優化目標是最小化未分配船舶的懲罰成本、泊位位置偏離成本與等待（靠泊時間與船舶到達時間之差）成本，其中船舶處理時間為一個固定值。Kim和Moon（2003）^[27]以最小化泊位位置偏離成本與延遲離港懲罰成本為目標建立了混合整數規劃模型，研究了動態情形下的泊位分配問題。船舶處理時間被視為一個固定值。Imai等（2005）^[28]與Chang等（2008）^[29]認為船舶裝卸時間取決于船舶所停靠的泊位位置。Lee等（2010）^[30]研究了船舶動態到港情況下的連續泊位分配問題，為每艘船舶分配一個權重，以最小化所有船舶加權的等待泊位時間與裝卸作業時間為目標建立了數學規劃模型，并設計了貪婪隨機適應性搜索算法進行求解；Zhen等（2011）^[31]在Kap Hwan Kim等（2003）^[27]研究的基礎上，引入了泊位分配的不確定性，并定義了一個基準點，此點之前到達的船舶無須調整，此點之后到達的船舶根據一定的概率調整靠泊位置和靠泊時間。Lee等（2009）^[32]認為船舶停靠有多個偏好區域，在偏好區域中尋找候選點，以候選點效用值最大化為目標建立了數學模型，兼顧先到先服務原則，最后采用鄰域搜索啟發式算法求解。韓曉龍等（2006）^[33]研究了船舶動態到港情形下的連續泊位分配問題，將泊位分配問題抽象為二維裝箱問題，認為船舶在港時間與所分配的岸橋數量呈反比，同時利用位置偏移系數對目標函數進行衡量，以船舶廣義在港時間最短為目標函數構建了數學模型，并設計了回溯算法求解。杜玉泉（2009）^[34]研究了“船舶到達時間不確定”與“有計劃外船舶臨時靠泊”兩種不確定性下連續泊位分配的干擾管理問題。何軍良等（2008）^[35]以靠泊位置偏離預定位置最小化為目標構建了數學規劃模型，采用分布式遺傳算法與啟發式算法相結合的分布式混合遺傳算法進行求解；李強等（2008）^[36]對連續泊位分配構建了混合整數規劃模型，其優化目標為最小化位置偏離成本、延期懲罰成本和加速裝卸成本，并設計了遺傳算法進行求解。Lee等（2009）^[37]考慮到先到先服務等原則，將等待時間轉化為效用函數，以效用最大化為目標，構建了混合整數規劃模型，并采用鄰域搜索算法求解。Du等（2011）^[38]在泊位分配模型中考慮到了能耗與車輛廢氣排放問題。Umang等（2013）^[39]以船舶在港時間最短為目標構建了混合整數規劃模型，對小規模問題設計了集分割算法，對大規模問題設計了吱吱輪算法。

1.2.2　岸橋作業調度

岸橋作業調度旨在將船舶上的裝卸作業任務合理地分配給岸橋，并確定每臺岸橋任務、作業序列及作業起止時間，從而達到既定目標。

Daganzo（1989）^[40]以最小化所有船舶裝卸作業總完工時間為目標，構建了混合整數規劃模型，分靜態與動態兩種情況對岸橋作業調度進行了研究。假設同一時間僅能有一臺岸橋在一個艙位作業，給出岸橋調度的3個原則：避免岸橋閑置、裝卸量最大的艙位（重點艙）優先分配及最大完工時間最短為首要目標。然而，岸橋空間干涉及移動時間并未被考慮在內。

Peterkofsky等（1990）^[41]也對船舶靜態情況下的岸橋作業調度進行了研究。以最小化所有船舶在港時間為目標，并運用分支限界法進行求解，同樣未考慮岸橋空間干涉與移動時間。

Lim等（2002）^[42]將空間干涉問題引入岸橋作業調度問題，假設船舶有數個艙，岸橋在艙間可自由移動，但同一時間僅能有一臺岸橋在一個艙位作業。對于空間干涉問題，主要通過岸橋與艙位相對位置的3個約束來實現，即禁止跨越約束（non-cross）、相鄰約束（neighborhood）及任務分割約束（job-separation），目的在于找出一個最佳的岸橋匹配及作業方案（crane-to-job matching and scheduling），使在固定時間內岸橋作業量（throughput）最大化；同時，也首次證明了以艙位為任務對象的岸橋作業調度問題為NP完全問題。

Lim等（2004）^[43]在2002年研究的基礎上，對岸橋作業調度進行了研究。作者將空間干涉明確劃分為不可跨越與安全距離兩種，目標同其2002年研究，但在具體作業時將任務劃分為若干個作業區域（areas），而非2002年研究中的艙位（holds），因此任務既可指同一艘船舶若干個艙位的裝卸作業，也可指若干個船舶的裝卸作業。

Zhu等（2006）^[44]考慮到碼頭作業實踐中總是希望盡可能早地完成船舶所有裝卸任務，將目標函數定為最小化船舶所有裝卸任務的最大完工時間，證明了該問題的NP完全性，并運用分支定界法來獲得小規模問題的精確解，對大規模問題則采用了模擬退火算法。

Lim等（2007）^[45]以船舶貝位裝卸作業為任務，將岸橋作業調度視為平行機調度問題，構建了一個混合整數規劃模型進行研究，目標函數為最小化裝卸作業的最大完工時間。岸橋作業調度被分為裝卸作業任務分配（job-to-crane allocation map）與任務時間分配（starting time allocation map）兩步解決，同時對兩者的性質進行了證明：任務時間分配取決于作業任務分配，一旦作業任務分配確定后，所對應的任務時間分配也將被確定下來。在模型求解方面，對于小規模問題，采用深度優先的搜索樹算法；對于大規模問題，則采用模擬退火算法。

Liu等（2006）^[46]以船舶貝位裝卸作業為任務對象，構建了一個混合整數線性規劃模型研究岸橋作業調度問題。作者考慮了岸橋初始位置、移動速度及空間干涉問題，目標函數為最小化船舶延遲離港時間。由于模型中規定所有岸橋采取單向移動，因此空間干涉問題得到了有效解決，模型的求解空間也得到了大大縮減，但這種假設的正確性仍有待進一步論證。

Lee等（2007）^[47]考慮了岸橋不可跨越限制，以船舶艙位裝卸作業為任務對象，構建了一個混合整數規劃模型，目標函數為最小化船舶裝卸作業的最大完工時間，但模型中并未考慮岸橋安全距離與移動時間。同時，證明了該問題屬于NP完全問題，因此不存在多項式時間的精確算法，并運用近似算法求得優化解。隨后，一個更加通用的啟發式算法——遺傳算法被用于解決這個問題。^[48]

Lee等（2008）^[49]研究了帶優先權的岸橋作業調度問題，此時，船舶貝位裝卸作業被賦予一定的優先關系，某些貝位必須先于其他貝位作業。在考慮岸橋不可跨越限制下，構建了混合整數規劃模型，目標函數為最小化所有貝位任務的總裝卸作業時間，并運用遺傳算法進行了求解。但在研究中，依然忽略了岸橋安全作業距離與移動時間。

Kim等（2004）^[50]從另外一個角度分析了岸橋作業調度問題。在這里，船舶裝卸作業任務不再以艙位或貝位為單位，而是更加細化，即一個貝位上的集裝箱根據任務屬性不同被分為若干個箱組（container group）。如進口集裝箱，以相同裝箱港或相同大小的箱子劃分為一組；出口集裝箱，以相同目的港或相同大小的箱子劃分為一組。作業時，同一貝位上的不同箱組遵循一定的原則：先卸載，再裝載。卸載時，甲板上的箱組優先；裝載時，艙內的箱組優先。岸橋必須完成同一屬性的箱組后才能進行下一個箱組的作業。作者還考慮到了岸橋不可相互跨越作業與安全距離。另外，兩個來源或目的地為同一堆場區的箱組，因會對堆場的場橋作業產生干擾，也無法同時進行。模型中，船舶靠泊、離港時間、岸橋指派及開工時間均為已知，岸橋作業調度問題旨在確定各岸橋的箱組作業序列及時間，以得到最小化裝卸作業最大完工時間的作業調度。目標函數為兩個目標的加權函數：目標1為最小化最大完工時間；目標2為所有岸橋的作業時間最短。隨后，運用分支定界法求得模型的最優解，但隨著問題規模的擴大，計算時間會快速增加，分支定界法將很難應用到實踐中，因此再以貪婪隨機適應性搜索算法（greedy randomized adaptive search procedure，GRASP）求解，克服了分支定界法在計算時間上的不足，找到了調度問題的近似最優解。

隨后，以箱組為作業任務的QCSP得到大量關注。Moccia等（2006）^[51]分析了Kim等（2004）^[50]研究中關于岸橋相互干擾約束的不足，認為在特殊情況下，該約束會失效，由此構建了新的規劃模型，并運用分支切割法（branch and cut）求解，該算法能在2個小時內求得最優解；Sammarra等（2007）^[52]針對Moccia等（2006）^[51]的模型，運用基于析取圖的禁忌搜索算法求解，該算法有效地降低了計算時間，且求解結果質量與Moccia等（2006）^[51]相差不大；Bierwirth等（2009）^[53]在分析Kim等（2004）^[50]、Moccia等（2006）^[51]、Sammarra等（2007）^[52]等研究的基礎上，認為其模型均不能有效地避免岸橋作業時的相互干擾，尤其是會違背岸橋不可相互跨越的限制，隨后構建了新的關于岸橋不可相互跨越作業的約束，并運用分支定界法進行了求解。

Ng等（2006）^[54]將船舶貝位上的集裝箱分為兩組：進口箱和出口箱。作者認為進口箱作業要優于出口箱。Steenken等（2001）^[55]將船舶劃分為若干個區域，每個區域都由連續的若干貝位組成，每臺岸橋負責一個區域的集裝箱作業。研究表明，這種做法可用集分割算法進行解決，也較容易應用到實際作業中。

此外，對于QCSP問題，還有少數文獻從其他角度進行了分析。Goodchild（2006）^[56]，以及Goodchild和Daganzo（2006，2007）^[57]，[58]以每一個貝位上的棧為作業任務對岸橋問題進行了研究。當岸橋在某一列進行卸箱的同時，也可在另一列進行裝箱，因此可避免岸橋的單向空駛，因此又被稱作雙線循環作業（邊裝邊卸）。岸橋作業調度旨在找出作業每一列集裝箱的最優序列，目的在于最小化最大完工時間。作者將該問題類比于兩臺機器的flow shop問題，并運用Johnson啟發式算法求解。Zhang等（2009）^[59]對此進行了擴展，不再局限于對同一個艙蓋板上的棧進行雙線裝卸，而是鄰近的艙蓋板上的棧均可進行雙線裝卸，以提高岸橋利用率并縮短船舶在港時間。Meisel等（2010）^[60]基于單箱對岸橋雙線作業進行了研究。Lu等（2012）^[61]以單箱作業為對象，基于連續貝位區域作業，構建了一個快速啟發式算法。Nguyen等（2013）^[62]設計了求解以箱組為任務對象的混合進化算法，具有良好的求解效果。Christopher等（2013）^[63]設計了求解岸橋作業調度問題的混合分布估計算法。Unsal等（2013）^[64]對岸橋作業調度建立了約束規劃模型。

國內關于岸橋作業調度的文獻較少，曾慶成等（2006）^[65]基于集裝箱組對岸橋作業調度進行了研究，以最小化最大完工時間為目標建立了模型，并運用貪婪隨機適應性搜索方法對遺傳算法進行了改進，減少了求解時間。韓笑樂等（2009）^[66]基于集裝箱貝位區域分析了岸橋作業調度。船舶依貝位被劃分為若干個區域，每個區域由若干個連續貝位組成。在各區域內部，存在一定的優先順序，每臺岸橋負責一個區域的集裝箱作業。作者考慮了設備調整時間，并采用了SPT（Shortest Processing Time）規則進行求解，但求解時間明顯過長。李晨等（2010）^[67]提出了一種能減少岸橋移動距離和均勻化岸橋負荷的啟發式算法。在該啟發式算法中，船舶被分為N個連續的區域，每個岸橋負責一個相應的區域，然后再均衡各岸橋任務量。接著，在該啟發式算法的基礎上，設計了遺傳算法進行求解。楊明珠（2011）^[68]對Kim等（2004）^[50]研究進行了算法改進，設計了新的貪婪隨機適應性搜索算法，在同樣的時間內能求得質量更好的解。董良才等（2011）^[69]考慮了裝卸過程中的艙蓋板作業，以箱組為單位分析了岸橋作業調度，并運用遺傳算法進行了求解。范志強等（2012）^[70]以貝位為任務對象從岸橋作業效率差異角度進行了研究，隨后將其擴展到以箱組為任務對象^[71]及從雙目標優化的角度（最小化最大完工時間與等待時間）進行了研究^[72]，求解方面均采用了遺傳算法。

1.2.3　泊位—岸橋指派—岸橋作業集成調度

因船舶作業時間與岸橋作業存在密切的關系，越來越多的學者將岸橋作業整合入泊位分配，形成了泊位—岸橋集成調度方式，但其整合方式與整合程度存在一定的差異。

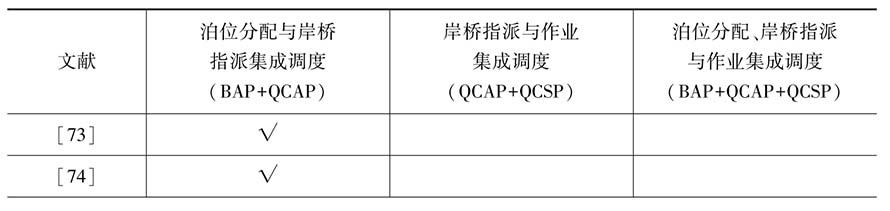
Park等（2003）^[73]將岸橋數量整合入泊位分配，形成了BAP＋QCAP（number，specific）整合方式。作者構建了泊位與岸橋作業調度成本模型，認為船舶裝卸作業時間與分配的岸橋數量存在很大的關系。若岸橋數量增加，則裝卸時間會減少，因此兩者需要同時考慮。相關重要假設如下：①每艘船舶有最多及最少岸橋指派數量；②裝卸時間與岸橋數量成反比；③早于預定靠泊時間或晚于預定離泊時間都需要付出懲罰成本。然后通過兩階段方法求解：第一階段，估計靠泊位置及岸橋數量，并利用拉格朗日松弛法與次梯度法來獲得近似解；第二階段，根據第一階段的求解結果，利用動態規劃對每臺岸橋的移動路徑進行詳細規劃。作者為簡化分析，假設裝卸時間與岸橋數量呈線性關系，即岸橋數量越多，裝卸時間越短；同時，并未考慮到岸橋空間干涉問題。實際上，服務于同一艘船舶的岸橋數量越多，相互干擾的概率就會越大，整個船舶裝卸的最大完工時間通常會減少，但最大完工時間與岸橋數量一定不會呈正比關系。

周鵬飛等（2008）^[74]將岸橋數量整合入泊位分配，形成了BAP＋QCAP（number）整合方式。作者研究了面向隨機環境的泊位分配—岸橋指派問題。相關重要部分假設如下：①船舶到港時間為隨機變量；②船舶裝卸時間依據所在泊位、岸橋數量等因素決定，為隨機變量；③船舶長度要滿足分配岸橋工作面要求，即分配岸橋數量不大于船舶允許同時作業的岸橋數量；④當多個岸橋同時裝卸一艘船舶時，不可避免地會造成彼此的干擾，進而影響岸橋的裝卸效率，因此選用最大允許岸橋數量與實際分配岸橋數量之差作為岸橋裝卸效率折減的依據，即0、1、2以上（包含2）相應的折減率分別為0.9、0.95、1.0。以船舶在港時間最短為目標建立了混合整數規劃模型，求解方面分為兩步：先為來港船舶分配泊位及靠泊順序，然后根據岸橋狀態為船舶分配岸橋。顯然，作者將船舶到港時間視為隨機變量，這在以前是普遍存在的，但現在的集裝箱船舶擁有固定的航線，在各個港口按照確定的班期循環往復地從事運輸活動，因此船舶到港時間已經基本固定^[75]；另外，作者考慮到了岸橋相互干擾因素，并用一個裝卸效率折減率對其描述，但顯然折減率并不能真實地反映岸橋裝卸情況。

Imai等（2008）^[76]研究了船舶動態到達情況下的離散泊位分配—岸橋指派問題，分析了BAP＋QCAP（number，specific）問題，其優化目標是最小化船舶在港時間（等待與裝卸時間）。Liang等（2009）^[77]研究了BAP＋QCAP問題，通過引入岸橋移動準則，以確定船舶的靠泊計劃、作業時間以及分配給每艘船舶的岸橋數目，其優化目標是作業時間、等待時間和延遲時間三者之和最小，并采用遺傳算法求解。Chang等（2010）^[78]研究了船舶動態到達情況下的連續泊位分配—岸橋指派問題（BAP＋QCAP），其優化目標是：①靠泊位置偏離最小；②延遲靠泊與離港的懲罰成本最小；③岸橋能源消耗最小。作者通過加權法將其轉化為單目標函數，并采用混合并行遺傳算法求解。Han等（2010）^[79]研究了船舶動態到達情況下的離散泊位分配—岸橋指派問題[BAP＋QCAP（number，specific）]，模型中船舶到達時間與裝卸作業時間均具有不確定性，提出了應對這種不確定性的主動調整方法，并采用了遺傳算法求解。韓曉龍（2005）^[80]研究了船舶動態到達情況下的連續泊位分配—岸橋指派問題，分析了BAP＋QCAP問題，其優化目標為計劃期內所有船舶的廣義時間[船舶實際在港時間×（1＋泊位偏離放大系數）]最短，并運用回溯法求解。韓駿等（2008）^[81]研究了離散型泊位和岸橋同時進行優化的問題（BAP＋QCAP），其優化目標是使所有船舶的總在港時間（等待與裝卸作業時間之和）最短，并采用了免疫遺傳算法進行求解。Yang等（2012）^[82]研究了船舶動態到達情況下的連續泊位分配—岸橋指派問題（BAP＋QCAP），并采用了遺傳算法求解。

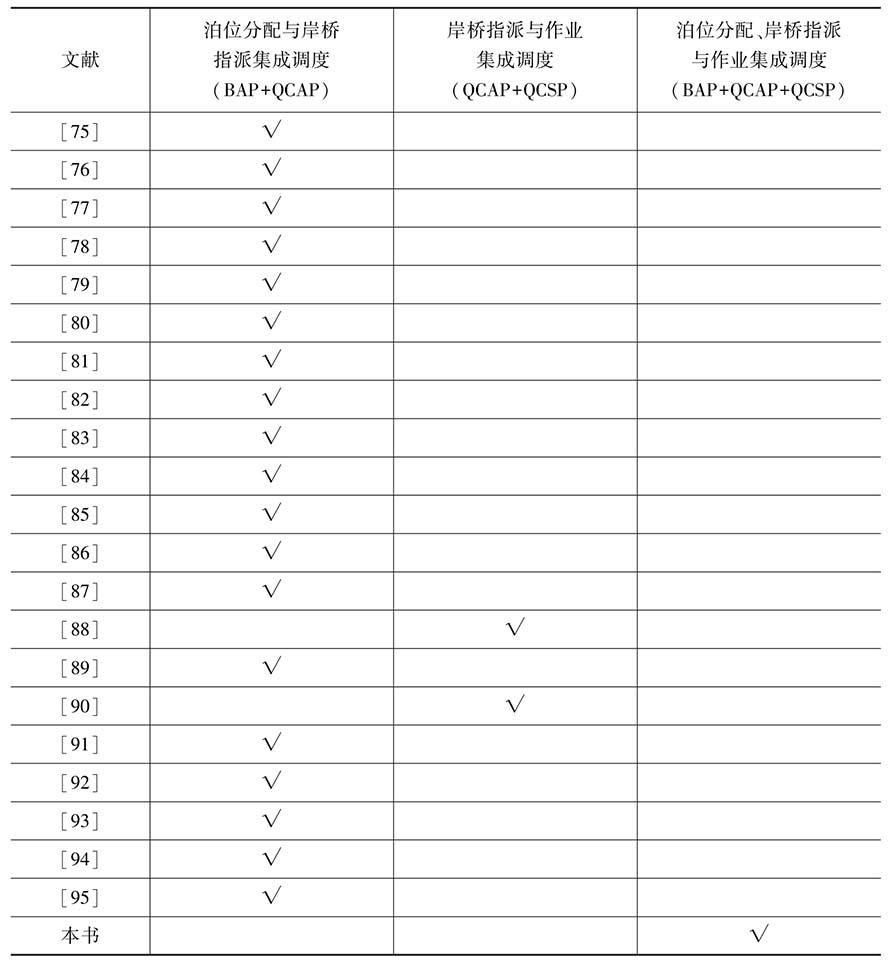
Raa等（2011）^[83]假設船舶裝卸作業時間取決于船舶所載集裝箱量與所分配的岸橋數量，對泊位分配問題與岸橋指派問題（BAP＋QCAP）進行了集成優化研究，構建了混合整數規劃模型，并設計了求解所用的啟發式算法。樂美龍等（2011）^[84]研究了連續泊位分配與岸橋指派集成優化問題（BAP＋QCAP），其優化目標為最小化船舶等待時間、裝卸作業時間與最小位置偏移量，并采用了Memetic算法求解。張紅菊等（2012）^[85]考慮了岸橋裝卸成本與位置偏離懲罰成本，以成本和時間最小化為目標，研究了連續泊位分配與岸橋指派優化問題（BAP＋QCAP），求解方面采用了粒子群算法。Meisel等（2009）^[86]在泊位分配問題中考慮到了岸橋生產效率（BAP＋QCAP），認為岸橋生產效率存在邊際遞減現象，并用一個折扣系數來描述多臺岸橋同時裝卸一艘船舶時的作業效率遞減情況，同時還考慮到了位置偏移所導致的裝卸作業時間增加的情形。李娜等（2011）^[87]研究了泊位調度與岸橋指派問題，假設只有船舶所需的岸橋數量達到規定的最小岸橋數量時才能作業。靳志宏等（2011）^[88]在假設泊位計劃已知的情況下，研究了岸橋調度問題；楊春霞等（2010）^[89]研究了泊位分配與岸橋指派問題，以船舶在港時間最短和碼頭運營成本最低為目標構建了數學模型，并通過多目標遺傳算法求解。Tavakkoli-Moghaddam等（2009）^[90]研究了岸橋指派與岸橋作業調度的集成優化問題。Elwany等（2013）^[91]以成本最小化為目標，研究了連續泊位分配與岸橋指派的集成調度問題。Giallombardo等（2010）^[92]研究了泊位分配與岸橋指派集成調度問題，構建了混合整數二次規劃模型，并基于禁忌搜索算法設計了啟發式算法求解。Turkogullari等（2013）^[93]研究了泊位分配與岸橋指派的集成調度問題，以成本最小化為目標，構建了混合整數規劃模型。Zhang等（2010）^[94]在泊位分配與岸橋指派問題研究中，考慮到了岸橋移動范圍的影響，以成本最小化為目標，構建了混合整數規劃模型。桂小婭等（2013）^[95]研究了連續泊位分配與岸橋指派的集成調度問題，以在港時間最短為目標構建了數學模型，并設計了雙層循環算法求解。

此外，還有很多學者的研究間接地與本書內容相關。計明軍等（2007）^[96]建立了集卡與岸橋集成調度模型，以最小化集卡運輸時間與岸橋作業時間之和為目標。作者在岸橋作業處理上，分為卸箱、裝箱與裝卸箱同時作業3種情況。陳璐等（2006）^[97]研究了岸橋—集卡—場橋的集成作業調度，假設船舶裝載作業在所有卸載作業完成之后再進行，并視作業為flow shop的擴展。

Imai等（2006）^[98]，Chen等（2007）^[99]，Canonaco等（2008）^[100]，周鵬飛（2005）^[101]，應俊（2011）^[102]，陳璐（2006）^[103]，樂美龍等（2012）^{[104]，[105]}，Tang等（2014）^[106]，Stahlbock等（2008）^[107]，Bierwirth等（2010）^[108]，他們分別從集卡調度、場橋調度、配載計劃等方面提到了岸橋作業調度，但這些研究的出發點并非優化岸橋作業序列，與本書的研究重點關系不大，因此不詳細論述。表1-1給出了現有集成調度研究文獻與本書所要研究內容的異同。

1.2.4　研究進展分析與總結

就研究現狀而言，泊位調度的研究文獻中，國外多以離散泊位調度為主，國內則以連續泊位調度為主。泊位調度存在著從離散泊位轉向連續泊位的趨勢，因為后者更有利于泊位資源的充分利用；另一個發展趨勢是泊位與其他資源的集成調度，如泊位與岸橋。岸橋作業調度則仍以單船裝卸作業調度為主，有2個研究趨勢：一是縱向方面，裝卸任務劃分不斷細化，從最初的多貝位區域（bay areas），到整貝（complete bays），接著是箱組（container group），直到最后的單箱（single container），目的在于更好地取得多臺岸橋的工作負荷均衡；二是橫向方面，與其他資源進行集成研究，如岸橋與泊位、岸橋與集卡、岸橋—集卡—龍門吊的集成優化調度等，這類研究仍然偏少，是未來的一個研究熱點。

就研究方法而言，現有泊位分配與岸橋作業調度均以構建混合整數規劃模型為主，鑒于問題的NP-hard特性，求解方面多采用智能優化算法或啟發式算法，如遺傳算法、禁忌搜索算法、模擬退火算法、粒子群算法等均有應用。

綜上所述，現有研究取得了重要進展與成果，在模型構建與求解方面為后續研究奠定了很好的基礎，但在一定程度上，為降低問題復雜程度，對問題做了簡化處理，致使調度方案與現實情況存在一定差距，主要包括：

（1）參數“船舶裝卸作業時間”的取值依據不合理

在單獨的泊位分配研究，以及泊位—岸橋集成調度研究中，一個重要的參數是“船舶裝卸作業時間”的取值問題，已有文獻研究多假定其為一固定常數，或與靠泊位置有關，或與岸橋數量呈反比，或在岸橋數量中加入一定的折扣率等，這類研究均以一個多項式函數來表示裝卸作業時間的大小，從而降低了問題的難度，對現實情況做了簡化處理。

（2）泊位—岸橋集成調度研究中忽略了具體的岸橋作業計劃

泊位與岸橋的集成調度研究已成為一個重要的發展趨勢，但現有文獻多以研究泊位分配與岸橋指派集成調度為主，而將具體的岸橋作業調度研究排除在外。事實上，這類研究得出的泊位計劃與岸橋指派方案，在執行過程中，要么存在泊位與岸橋資源嚴重閑置情況，要么出現在計劃的泊位窗口期內，根本無法完成具體的岸橋作業調度情況，其主要原因在于忽略了具體的岸橋作業計劃。

（3）關于泊位分配、岸橋指派與岸橋作業調度的集成研究偏少

由于建模與求解難度的增加，現有研究較少將三者進行集成調度研究。由前面的分析可知，泊位分配、岸橋指派與岸橋作業調度三者之間是相互聯系、相互影響的。因此，三者的集成調度研究應是一個重點發展方向，其建模與算法需要進一步的研究。