第2章 引力不是力
牛頓完全意識到了他理論中關(guān)于絕對空間的問題,但他認(rèn)為加速度(特別是旋轉(zhuǎn)) 是可以解決這個問題的秘密武器。為了先發(fā)制人,他提出了一個思想實驗,表明旋轉(zhuǎn)運動證明了絕對空間的存在,這就是牛頓著名的“水桶實驗”。
是可以解決這個問題的秘密武器。為了先發(fā)制人,他提出了一個思想實驗,表明旋轉(zhuǎn)運動證明了絕對空間的存在,這就是牛頓著名的“水桶實驗”。
在《自述》(Autobiographical Notes)中,愛因斯坦對此事只是順便提了一下:“首先要提到的是馬赫的論述,雖然牛頓早就清楚地認(rèn)識到了(指水桶實驗)。”
愛因斯坦《狹義與廣義相對論淺說》的附錄五中并沒有提到牛頓的水桶實驗,但他認(rèn)為奧地利人恩斯特·馬赫(Ernst Mach)是唯一“認(rèn)真考慮了如何消除空間概念的物理學(xué)家,馬赫嘗試代之以特定時刻所有質(zhì)點之間距離的總和(他提出的這個概念,后來成了對慣性的完美的描述)”。
我們可以這樣理解牛頓的思想實驗:我們將繩子一頭系在水桶的把手上,另一頭高高地掛在樹枝上,這樣水桶就懸掛在空中了。往水桶里加3/4容量的水,然后不斷旋轉(zhuǎn)水桶,讓繩子扭曲,直到繩子扭曲到不能再扭曲了,我們就松手,看看會發(fā)生什么(如圖3所示)。
繩子開始解旋,水桶開始旋轉(zhuǎn)。一開始,桶中的水仍然保持靜止。接著,隨著桶旋轉(zhuǎn)速度的增加,桶里的水也開始旋轉(zhuǎn),水面凹了進去。這是由于旋轉(zhuǎn)運動給水施加了離心力,讓水向外運動,因此越靠近桶壁水位就越高。最終,水旋轉(zhuǎn)的速度趕上了桶旋轉(zhuǎn)的速度,水和桶一起旋轉(zhuǎn)。
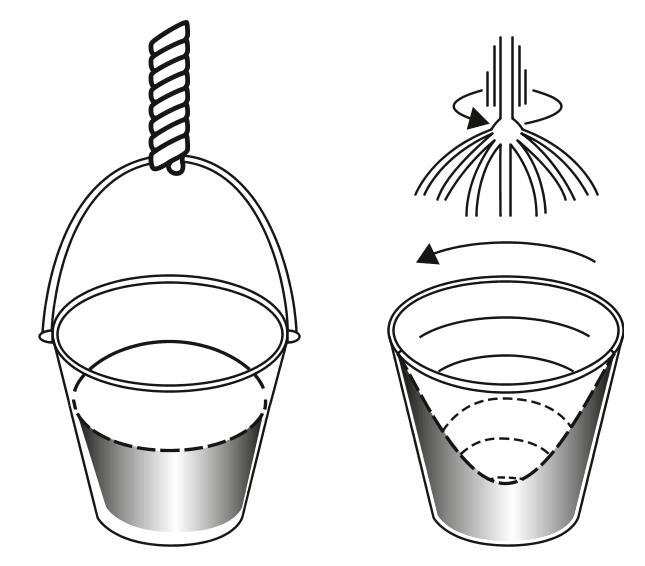
圖3 牛頓水桶實驗的示意圖(隨著繩子解旋,桶開始旋轉(zhuǎn),里面的水被從中心拉向桶壁一側(cè),呈現(xiàn)凹陷的形狀)
在《自然哲學(xué)的數(shù)學(xué)原理》中,牛頓寫道:
桶壁一側(cè)水位的上升,表明水會努力向離旋轉(zhuǎn)軸更遠的地方運動。這表明,水的旋轉(zhuǎn)運動是真實的、絕對的,而不是相對的。通過這種運動,我們就可以定義并測量絕對運動。
這是我們?nèi)粘I钪谐R姷钠毡楝F(xiàn)象,你可能會覺得它什么都不能證明,更別提證明絕對空間了。但牛頓推理的邏輯是令人信服的。水從內(nèi)向外移動并沿著桶壁上升的過程顯然是一種運動,這種運動要么是絕對的,要么是相對的。只要水和桶的旋轉(zhuǎn)速度存在差值,水就會繼續(xù)由內(nèi)而外,沿著桶壁上升,并且在速度相同時保持這個形狀不變。牛頓認(rèn)為,水的這一行為不能歸因于水與桶的相對運動。如果這一運動不是相對的,那它必定是絕對的,而如果存在絕對運動,絕對空間就必然存在。
愛因斯坦意識到了牛頓推理中的邏輯缺陷,但他的反駁需要我們花一點兒力氣才能理解。多年以后,人們意識到,牛頓沒有縱觀全局。桶中水的行為確實不能只由它相對桶的運動來解釋,但是可以由它相對于整個宇宙中其他部分的運動來解釋。
之前提到過,如果所有的運動(包括旋轉(zhuǎn))都是相對的,那么我們原則上就不可能通過觀察或測量區(qū)分是哪個人或者哪個物體在運動。這就是相對運動的含義。如果我們不能區(qū)分是桶相對于整個宇宙的其他部分在旋轉(zhuǎn),還是整個宇宙的其他部分在繞著桶旋轉(zhuǎn),牛頓的論證就不成立了。
當(dāng)然,如果是整個宇宙的其他部分繞著靜止的桶旋轉(zhuǎn),就說明這讓桶中的水受到了離心力。但我們得思考這是怎么做到的。
愛因斯坦的評論清楚地表明,反駁牛頓的這一觀點主要來自物理學(xué)家、頭號經(jīng)驗主義者馬赫,這一觀點也被稱為馬赫原理 。為了完全抹除絕對空間的概念,愛因斯坦需要找到一個情境,在這個情境中,正在加速運動的觀察者無法分辨出是誰或者什么東西正在加速。
。為了完全抹除絕對空間的概念,愛因斯坦需要找到一個情境,在這個情境中,正在加速運動的觀察者無法分辨出是誰或者什么東西正在加速。
所有在地球上的人都會認(rèn)為加速度(或者慣性,它衡量的是物體抵抗運動狀態(tài)變化的傾向)是我們可以直接感受到的,因此是絕對的、無可爭辯的。但如果我們是在太空中自由下落呢?
我們不知道愛因斯坦當(dāng)時正在想什么,但我們知道,在1907年11月那平凡的一天,愛因斯坦在瑞士專利局邂逅了他“一生中最幸福的思想” 。當(dāng)時的愛因斯坦已晉升為“二級技術(shù)專家”。他后來回憶道:“我當(dāng)時坐在位于伯爾尼的瑞士專利局的椅子上,突然一個想法擊中了我:如果一個人自由下落,他將感受不到自己的重量。我大吃一驚,這個簡單的思想實驗對我產(chǎn)生了極大的影響。”
。當(dāng)時的愛因斯坦已晉升為“二級技術(shù)專家”。他后來回憶道:“我當(dāng)時坐在位于伯爾尼的瑞士專利局的椅子上,突然一個想法擊中了我:如果一個人自由下落,他將感受不到自己的重量。我大吃一驚,這個簡單的思想實驗對我產(chǎn)生了極大的影響。”
在自由落體運動中,人既感受不到加速度,也感受不到重力。從這個非常簡單的直覺出發(fā),愛因斯坦意識到,我們對于加速度的感覺,與我們對重力(引力)的感覺是完全一樣的,它們就是同一件事。愛因斯坦把這條原理稱為等效原理。這意味著,解決了加速度的相對性問題,也許可以同時解決牛頓引力的問題。或許,本來待解決的就不是兩個不同的問題,而是一個。斯莫林依然記得當(dāng)年在乘紐約地鐵時閱讀愛因斯坦1907年發(fā)表的關(guān)于等效原理的論文的事,他稱自己“突然明白了” 。
。
愛因斯坦發(fā)現(xiàn)了等效原理,卻不知道該拿它來做什么。不管怎么樣,到1907年年末,他的生活有了很大的改變。隨著他的知名度日益增長,他開啟了學(xué)術(shù)事業(yè),先后在蘇黎世和布拉格的大學(xué)任教。愛因斯坦承擔(dān)了很多教學(xué)與管理的工作,研究興趣也轉(zhuǎn)向了其他物理學(xué)問題。又過了5年,他才意識到等效原理可以幫助他在另外兩件事物間建立聯(lián)系:引力與幾何。
與引力有關(guān)的是什么東西的幾何形狀呢?1908年,愛因斯坦之前在蘇黎世理工學(xué)院的數(shù)學(xué)教授赫爾曼·閔可夫斯基(Hermann Minkowski)意識到,可以將空間和時間通過某種方式組合起來,讓狹義相對論中的時間延緩和距離縮短效應(yīng)可以互補,從而產(chǎn)生了四維的時空,人們有時也稱之為時空度量。
愛因斯坦后來花了很大力氣才證明,這種“四維”的時空觀并不是新事物。在牛頓的經(jīng)典物理學(xué)中,日常發(fā)生的每一件事都需要4個數(shù)才能完全描述:三個空間坐標(biāo)x、y、z,以及一個時間坐標(biāo)t。但牛頓物理學(xué)把時間當(dāng)成一個截然不同的量,并相較于空間獨立處理。而在閔可夫斯基的時空中,時間t(單位為秒)與光速c(單位為米每秒)相乘后,ct的單位與空間坐標(biāo)x、y、z相同(均為米),所以時間與三個空間坐標(biāo)擁有平等的地位。
如果引力與加速度等效,那么牛頓在伍爾斯索普莊園的花園中被蘋果砸到頭的經(jīng)歷(廣為流傳但真實性可疑)就可以從兩種不同但等價的角度來看待。我們可以想象引力通過某種方式作用于蘋果,將蘋果拉向地面,也可以想象地面向上加速以迎接蘋果。這兩種角度是等效的,但后者只在我們將地球想象成平的時才成立。當(dāng)然,地球是圓的,我們可不能對地球另一面的人們不管不顧。
愛因斯坦開始意識到,問題在于時空本身。閔可夫斯基時空是平直的歐幾里得空間,以古希臘著名數(shù)學(xué)家歐幾里得命名。我們在學(xué)校里學(xué)到三角形的內(nèi)角和為180°,圓的周長是其半徑的2π倍,兩條平行線永不相交,這些都是平直空間的特征。當(dāng)我們給三維空間加上第四維——時間,就得到了一個平直的時空。
愛因斯坦擅長跳出思維定式來想問題,而且以往他的這種思維方式通常都取得了驚人的效果。如果把地球看成平的,它在穿過平直時空的過程中就能實現(xiàn)加速度與引力的等效性。但我們知道地球表面是個彎曲的球面,所以,如果時空是彎曲的呢?
在平直的時空里,兩點之間的最短距離顯然是連接兩點的線段長度。但倫敦和悉尼之間的最短距離(10553英里 )可不是連接兩個城市的線段長度。在球面上,這兩點之間的最短距離來自一條被稱為“大圓弧線”或“測地線”的彎曲路徑。
)可不是連接兩個城市的線段長度。在球面上,這兩點之間的最短距離來自一條被稱為“大圓弧線”或“測地線”的彎曲路徑。
這就是愛因斯坦曾經(jīng)尋找的答案。在平直空間中,所有線都是直的,因此牛頓的引力必然能瞬間跨過一段距離發(fā)生作用。但如果時空是彎曲的,就像大圓弧線一樣,那么沿著這條路徑運動的物體就是在“自由落體”,在自由落體的過程中,它就獲得了加速度。
愛因斯坦偉大的洞察力在于,他想到了時空并不是固定不變的,而是可塑的。就像磁場的“力線”一樣,時空可以根據(jù)質(zhì)能的存在這樣或那樣地彎曲。一個像恒星那樣的大型物體會彎曲它周圍的時空(如圖4所示),就好像一個小孩在蹦床上跳來跳去時會改變蹦床表面的形狀一樣。其他物體,例如行星,一旦離恒星過近,就會沿著時空形狀所決定的最短路徑運動。沿著最短路徑做自由落體運動的行星就獲得了加速度,這與行星受到引力而獲得加速度是完全等價的。
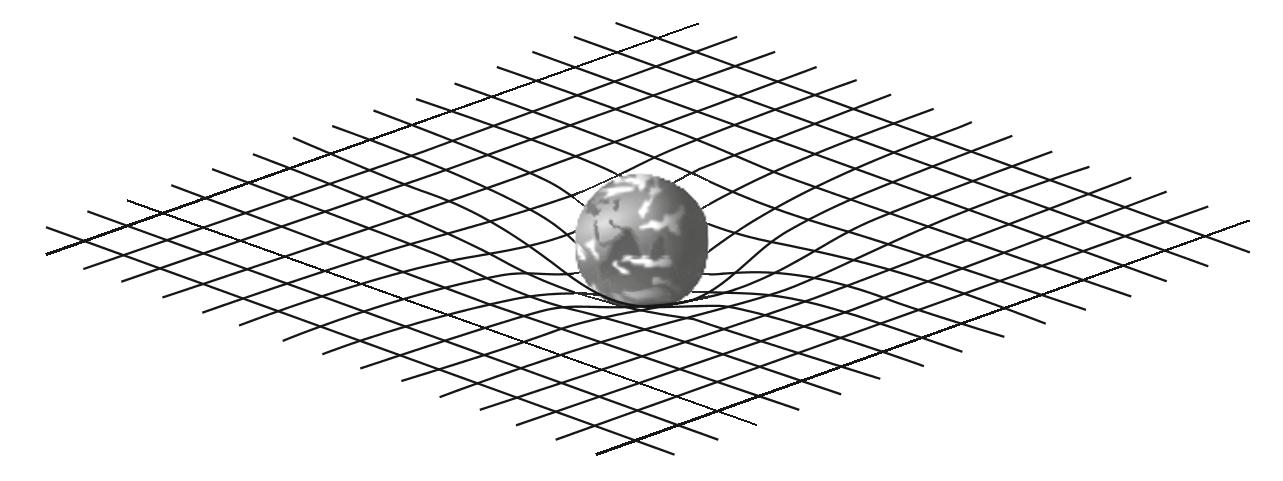
圖4 一個有著較大質(zhì)能的物體,例如地球,會讓它周圍的時空彎曲
掉落的蘋果并不必須被看作是某種神秘的超距作用力從地底下憑空而起將其拽落,它也可以被看作是愉快地沿著地球質(zhì)量造成的彎曲時空給出的最短路徑,一路加速而落地。
1952年5月,普林斯頓大學(xué)的美國理論物理學(xué)家約翰·惠勒(John Wheeler)從書架上拿下一個裝訂精致的全新筆記本,并給它寫上“相對論Ⅰ”的標(biāo)簽。他很滿意學(xué)校同意他教一門關(guān)于相對論的課程,并且想通過撰寫一本教材來好好研究一下這個課題。“那年秋天,有15名研究生選了我的這門課,”惠勒說,“這是普林斯頓大學(xué)第一次開設(shè)相對論的課程。我和學(xué)生一起深入研究了這個課題,嘗試透過已經(jīng)主導(dǎo)該理論數(shù)十年的數(shù)學(xué)形式,尋找真正的、觸手可及的物理意義。”
這本書最終于1973年出版,題為《引力論》(Gravitation),由惠勒與查爾斯·米斯納(Charles Misner)和基普·索恩(Kip Thorne)合著。在罕布什爾學(xué)院讀大學(xué)的第一年,斯莫林參加了人生中的第一次科學(xué)會議——兩年一度的得克薩斯相對論天體物理學(xué)專題討論會系列中的一場,在紐約市舉行。在會上,他遇到了牛津大學(xué)的數(shù)學(xué)物理學(xué)家羅杰·彭羅斯(Roger Penrose),還聽了史蒂芬·霍金和美國理論物理學(xué)家布賴斯·德威特(Bryce DeWitt)的報告。斯莫林也遇到了索恩,索恩建議他弄到這本新出版的《引力論》并認(rèn)真吃透它。雖然這本書并不是大學(xué)課程要求的教材,但在接下來的一年里斯莫林還是對著它仔細研讀。
這本書注定成為一本極有影響力的教材。它有近1 300頁,厚厚的一大本,非常適合幫助思維方式較為實際的學(xué)生掌握引力的圖像——如果它沿著時空的彎曲掉落,著地的時候會發(fā)出重重的一聲悶響。
在找到合適的措辭之后,惠勒在幾年后總結(jié)了愛因斯坦的相對論:“時空告訴物質(zhì)如何運動,物質(zhì)告訴時空如何彎曲。”
借助這樣的洞察力,愛因斯坦發(fā)現(xiàn)了可以同時解決加速度和引力問題的理論,即后來我們所說的廣義相對論。廣義相對論表明,引力這種東西并不存在。質(zhì)能產(chǎn)生引力場,但引力場并不與磁場類似:它不是存在于時空中每一點的某種東西。引力場本身就是時空。
想法已經(jīng)有了,但愛因斯坦需要找到一種方法用數(shù)學(xué)的語言把它表達出來。把想法轉(zhuǎn)化成數(shù)學(xué)公式總是困難的,研究四維空間中的物理學(xué)則格外困難,但愛因斯坦急需一套方程組來解釋所有種類的時空幾何形狀。他的理論需要適應(yīng)各種各樣的時空,而它們的坐標(biāo)方向可能各不相同。
愛因斯坦進一步提出了兩條原理來推進自己的研究。其一是廣義協(xié)變性,其本質(zhì)上是相對性原理的延伸,保證物理學(xué)定律與參考系的選擇完全無關(guān)——不管是慣性系還是有加速度的非慣性系都是如此,因此也與坐標(biāo)系的選擇無關(guān)。
第二條原理叫作一致性原理。愛因斯坦承認(rèn),牛頓萬有引力定律的精度在它的適用范圍內(nèi)是完全沒有問題的,因此他要求引力場方程能在極限條件下導(dǎo)出牛頓引力定律,即空間平直、速度遠低于光速的條件下。
有一種廣泛的誤解認(rèn)為,愛因斯坦是一位天才的物理學(xué)家,也必定是一名優(yōu)秀的數(shù)學(xué)家,然而他并不是。他在將廣義相對論的思想數(shù)學(xué)化時遇到了困難,并求助于朋友馬塞爾·格羅斯曼(Marcel Grossman),格羅斯曼向他介紹了偉大的德國數(shù)學(xué)家卡爾·弗里德里希·高斯(Carl Friedrich Gauss)及其學(xué)生伯恩哈德·黎曼(Bernhard Riemann)的工作。愛因斯坦接觸到了黎曼的曲率張量,這是描述任意坐標(biāo)系下一般幾何形狀曲率的標(biāo)準(zhǔn)數(shù)學(xué)表達方式。正是這一聯(lián)系,后來讓16歲的斯莫林的興趣從建筑轉(zhuǎn)向了廣義相對論。
但黎曼張量并不能很好地滿足愛因斯坦的要求。而且,在努力總結(jié)廣義相對論的數(shù)學(xué)形式的過程中,愛因斯坦被艱深復(fù)雜的代數(shù)形式搞迷糊了。在兩年間,他犯了各種各樣的錯誤,嘗試走了很多條路,但每條通往的都是死胡同。
最終,愛因斯坦還是找到了能描述引力場,并滿足他對物理學(xué)原理的所有需求的數(shù)學(xué)形式。其結(jié)果是一系列方程,將時空的彎曲(位于方程左側(cè))與質(zhì)能的分布和流動(位于方程右側(cè))聯(lián)系了起來。他在位于柏林的普魯士科學(xué)院做了四場講座(最后一場在1915年11月25日舉行),將自己的這一系列方程公之于眾。
從開始構(gòu)思到最終得到廣義相對論的引力場方程為止,愛因斯坦想出了四種手段以驗證這一理論。
第一種與其說是驗證手段,不如說是對已有疑難問題的解決。從約翰內(nèi)斯·開普勒(Johannes Kepler)17世紀(jì)提出開普勒三定律時我們就知道,行星圍繞太陽運行的軌道呈橢圓形。但行星軌道并不是完美的橢圓——如果是那樣的話,行星軌道上距離太陽最近的那個點(近日點)應(yīng)該是固定不動的,行星每繞一圈時都在這個位置離太陽最近。然而,天文觀測表明,行星每運行一周時,近日點都會產(chǎn)生微小的偏移,這種現(xiàn)象被稱為進動。
天文學(xué)家觀測到的進動,一大部分可以用太陽系中其他行星的引力總和來解釋,這是牛頓定律完全可以解釋的現(xiàn)象。對于離太陽最近的水星來說,牛頓力學(xué)預(yù)言的進動為每世紀(jì)532角秒 。然而,實際觀測到的進動值要更大一些,大約為每世紀(jì)574角秒,兩者相差42角秒。這個差值雖然很小,但它意味著每300萬年水星都要多轉(zhuǎn)一圈。
。然而,實際觀測到的進動值要更大一些,大約為每世紀(jì)574角秒,兩者相差42角秒。這個差值雖然很小,但它意味著每300萬年水星都要多轉(zhuǎn)一圈。
牛頓力學(xué)無法解釋這一差異,有人提出了其他解釋,比如在水星軌道的內(nèi)側(cè)還存在一顆離太陽更近的行星,稱為祝融星(Vulcan),天文學(xué)家苦苦找尋它無果。愛因斯坦高興地發(fā)現(xiàn),用場方程計算出來的相對論效應(yīng),剛好貢獻了每世紀(jì)43角秒的差值,這是因為水星離太陽太近,受到了太陽周圍時空彎曲的影響。 這一發(fā)現(xiàn)讓愛因斯坦獲得了一生中在科學(xué)上所獲得的最強烈的情緒體驗:“一連幾天,我都因喜悅和激動而發(fā)狂。”
這一發(fā)現(xiàn)讓愛因斯坦獲得了一生中在科學(xué)上所獲得的最強烈的情緒體驗:“一連幾天,我都因喜悅和激動而發(fā)狂。”
或許廣義相對論最著名的預(yù)言還要數(shù)星光在經(jīng)過太陽時的彎曲。和水星的進動一樣,星光彎曲本身并不是一個新的預(yù)言,但廣義相對論預(yù)言的是彎曲的程度。牛頓的引力定律表明經(jīng)過太陽表面的光應(yīng)該彎曲0.85角秒 ,但廣義相對論的時空彎曲預(yù)言的數(shù)值是它的兩倍——1.7角秒。與水星進動不同,沒有人測量過星光從太陽旁邊經(jīng)過時彎曲的程度,因此這會是一場直接的檢驗。
,但廣義相對論的時空彎曲預(yù)言的數(shù)值是它的兩倍——1.7角秒。與水星進動不同,沒有人測量過星光從太陽旁邊經(jīng)過時彎曲的程度,因此這會是一場直接的檢驗。
眾所周知,愛因斯坦的預(yù)言由英國天體物理學(xué)家阿瑟·愛丁頓(Arthur Eddington)帶領(lǐng)的一個團隊于1919年5月驗證。他們在日全食期間測量了多個恒星發(fā)出、經(jīng)過太陽再到達地球的光。盡管幾乎沒有人真正理解時空彎曲真正的含義(其中更是幾乎沒有人能看得懂抽象的張量數(shù)學(xué),哪怕專業(yè)的物理學(xué)家中也沒有幾個人能懂),但時空彎曲的概念激發(fā)了大眾的想象力,愛因斯坦一夜成名。
廣義相對論還預(yù)言了彎曲時空帶來的類似狹義相對論的效應(yīng),愛因斯坦在1911年就計算出了個中細節(jié)。他推導(dǎo)出,在大型物體附近,即時空彎曲得最厲害的地方,測量到的時間會延緩,距離也會收縮。一個放置于地球表面的標(biāo)準(zhǔn)鐘會比在地球上空的軌道上飛行的鐘走得慢。
我們在上一章中了解:如果把一臺原子鐘放在飛機上,從英國倫敦運到美國華盛頓特區(qū)再運回來,它就會比一直靜止地放在英國國家物理實驗室的鐘慢1.6×10–8秒。這種時間延緩是飛機的速度帶來的,屬于狹義相對論的效應(yīng)。但這臺鐘在高于海平面10千米的空中飛行時受到的重力要比地面小,即時空彎曲程度小,因此廣義相對論效應(yīng)會使它再慢5.3×10–8秒。經(jīng)過一些幾何學(xué)上的調(diào)整之后,最終理論預(yù)測鐘會慢4.0×10–8秒。2005年,科學(xué)家進行了這一實驗,測得鐘慢了(3.9±0.2)×10–8秒。
你可能會覺得千萬分之一秒的誤差對于我們地球上的日常生活而言根本不值一提,但如果不修正狹義和廣義相對論帶來的微弱效應(yīng),你的智能手機應(yīng)用軟件、車載導(dǎo)航、船或飛機上用的全球定位系統(tǒng)(GPS)的誤差很快就會開始積累,僅在一天內(nèi)就會造成11千米的定位誤差。 繪制你的跑步或騎車路線圖將會很困難,在海上的船和在空中的飛機也都要迷路了。
繪制你的跑步或騎車路線圖將會很困難,在海上的船和在空中的飛機也都要迷路了。
愛因斯坦的場方程極為復(fù)雜,以至于愛因斯坦本人都認(rèn)為它們不可能在不做簡化近似的條件下被精確求解。然而,才不到一年,德國數(shù)學(xué)家卡爾·施瓦西(Karl Schwarzschild)就得出了一組解。施瓦西的解描述了一類大的、不帶電的、非旋轉(zhuǎn)的球形物體,可以作為緩慢旋轉(zhuǎn)的天體(如恒星和行星)的有效近似。斯莫林在進入罕布什爾學(xué)院不久后就選了施瓦西解作為口頭匯報的課題,結(jié)果事實證明他高估了自己的能力,理解上的不足很快就暴露了出來,最后他這門課沒能及格 。
。
施瓦西解最驚人的特征之一是它們預(yù)言了一道基本的邊界,被稱為施瓦西半徑。任何被壓縮到半徑小于其施瓦西半徑的物體都會達到極大的密度,以至于它周圍的時空被彎曲到落回自身(地球的施瓦西半徑約為9毫米)。沒有任何事物能夠逃出這類物體的引力場,連光都不行。這類物體就是黑洞 。
。
羅韋利在多年后寫道:“當(dāng)我還在讀大學(xué)的時候,黑洞被認(rèn)為是一種晦澀難懂的理論所預(yù)言的難以想象的可能的結(jié)果。而如今,天文學(xué)家已經(jīng)觀測到成百上千個黑洞,并且開始研究它的細節(jié)了。” 盡管黑洞顯然難以直接探測到,但如今有大量間接證據(jù)表明,這種東西在我們的宇宙里存在得相當(dāng)普遍,而且或許每個星系的中心都有特大質(zhì)量黑洞。
盡管黑洞顯然難以直接探測到,但如今有大量間接證據(jù)表明,這種東西在我們的宇宙里存在得相當(dāng)普遍,而且或許每個星系的中心都有特大質(zhì)量黑洞。
愛因斯坦對于黑洞的想法表現(xiàn)得較為冷靜,但1916年6月他推測,引力場的小波動會在時空中形成波并向外傳播,就像湖面的水波一樣。 這類引力波與光波截然不同,只能在兩個大質(zhì)量天體相互繞轉(zhuǎn)(天文學(xué)家稱之為雙星系統(tǒng))的情況下產(chǎn)生。直到20世紀(jì)五六十年代,物理學(xué)家才意識到他們有機會實實在在地探測到引力波,而在2015年9月15日,他們的耐心終于得到了回報。
這類引力波與光波截然不同,只能在兩個大質(zhì)量天體相互繞轉(zhuǎn)(天文學(xué)家稱之為雙星系統(tǒng))的情況下產(chǎn)生。直到20世紀(jì)五六十年代,物理學(xué)家才意識到他們有機會實實在在地探測到引力波,而在2015年9月15日,他們的耐心終于得到了回報。
2015年9月15日,一個叫LIGO的合作實驗組織觀測到了兩個黑洞并合時發(fā)出的引力波。LIGO包含兩座觀測臺,一座位于美國路易斯安那州的利文斯頓,另一座位于華盛頓州里奇蘭附近的漢福德,幾乎位于美國本土的對角線兩端。LIGO的觀測結(jié)果于2016年2月11日公布,從那時候開始,LIGO和位于意大利比薩的天文臺Virgo一起,繼續(xù)記錄下了一些引力波事件,其中包括兩個中子星并合的事件。2017年諾貝爾物理學(xué)獎頒給了美國物理學(xué)家巴里·巴里什(Barry Barish)、基普·索恩和雷納·韋斯(Rainer Weiss),以表彰他們對LIGO和引力波觀測做出的貢獻。
成功探測到引力波不僅強有力地證明了廣義相對論的正確性,也打開了探索宇宙中遙遠事件的新窗口,我們無須依賴光或其他形式的電磁輻射就可以知道發(fā)生了什么。
當(dāng)愛因斯坦在普魯士科學(xué)院做關(guān)于廣義相對論的系列講座的最后一場時,他相信自己已經(jīng)完全解決了絕對空間和時間的問題。他寫道:“(廣義相對論的廣義協(xié)變原理)將物理客觀性的最后一片遺跡從時間和空間中消除了。” 因此,他宣布,絕對時空觀失敗了,相對論勝利了。
因此,他宣布,絕對時空觀失敗了,相對論勝利了。
讓我們回到馬赫原理,如果牛頓的桶是靜止的,而宇宙其他部分圍繞它旋轉(zhuǎn),那是什么造成了把水沿著桶壁向上推的離心力呢?
答案會讓你驚嘆不已。我們認(rèn)為靜態(tài)的水之所以會隨著桶轉(zhuǎn)動起來,是因為整個宇宙的質(zhì)能一起拽動了它周圍的時空。這一效應(yīng)在1918年由奧地利物理學(xué)家約瑟夫·倫澤(Josef Lense)和漢斯·蒂林(Hans Thirring)由廣義相對論導(dǎo)出,被稱為參考系拖曳(framedragging),又稱倫澤–蒂林效應(yīng)。參考系拖曳效應(yīng)告訴我們,我們確實不可能通過測量來區(qū)分到底是水在靜態(tài)的宇宙中旋轉(zhuǎn),還是整個宇宙繞著在桶中靜止的水旋轉(zhuǎn)。水的旋轉(zhuǎn)運動是相對的。
2004年4月24日,一座被稱為引力探測器B(Gravity Probe B)的極為精密的設(shè)備被發(fā)送到了極地軌道上。這顆衛(wèi)星上搭載了4臺陀螺儀,在衛(wèi)星繞地球旋轉(zhuǎn)的過程中,科學(xué)家密切監(jiān)測著陀螺儀的方向,并觀察到了兩種效應(yīng)。地球使其周邊的時空發(fā)生彎曲,根據(jù)預(yù)測,這將使引力探測器B上的陀螺儀在繞地球軌道平面上(即南北方向)發(fā)生6 606毫角秒 /年的進動。這一進動被稱為測地漂移(geodetic drift),該現(xiàn)象由荷蘭物理學(xué)家威廉·德西特(Willem de Sitter)在1916年發(fā)現(xiàn)。
/年的進動。這一進動被稱為測地漂移(geodetic drift),該現(xiàn)象由荷蘭物理學(xué)家威廉·德西特(Willem de Sitter)在1916年發(fā)現(xiàn)。
第二種效應(yīng)就是參考系拖曳。隨著地球繞著地軸旋轉(zhuǎn),它沿著東西方向(垂直于引力探測器B的軌道平面)拖動了周圍的時空,這會讓引力探測器B上的陀螺儀產(chǎn)生第二種進動,據(jù)預(yù)測應(yīng)為39.2毫角秒/年。
數(shù)據(jù)采集從2004年8月開始,大約一年之后結(jié)束。該項目遭遇了一場令人失望的意外:由于發(fā)生了此前未曾預(yù)料到的靜電荷的累積,衛(wèi)星上的陀螺儀產(chǎn)生了令人意想不到的大幅擺動。這項誤差可以用一套精細的數(shù)學(xué)模型來校正,但代價是增加了最終實驗結(jié)果的不確定度。
對數(shù)據(jù)的分析持續(xù)了5年。2011年5月4日,研究人員在一場新聞發(fā)布會上公布了實驗結(jié)果:測地漂移為6 602±18毫角秒/年,參考系拖曳在東西方向上產(chǎn)生的漂移為37.2±7.2毫角秒/年。后者的不確定度如此大,正是校正陀螺儀擺動的數(shù)學(xué)模型帶來的。
盡管不確定度較大,但這一實驗結(jié)果也為廣義相對論增添了一項有力的證據(jù)。
對于20世紀(jì)70年代末學(xué)習(xí)相對論的學(xué)生而言,有很多驗證相對論的經(jīng)驗證據(jù)還沒有出現(xiàn)。但哪怕是最叛逆的學(xué)生,都不會質(zhì)疑相對論本質(zhì)上的正確性。誠然,這一理論的確復(fù)雜,它使用的數(shù)學(xué)語言只有很少的一部分人才有能力理解,但它在概念上的優(yōu)美性或許在整個物理學(xué)史上都是無可匹敵的。相對論仿佛會施魔法,斯莫林和羅韋利都被它迷住了。“它是通往真實的一瞥。或者說,它就是對真實的一瞥,比我們?nèi)粘?吹降哪:接沟木跋蟾鼮榍逦M高^它看到的世界與我們夢中的世界有著同樣的組成,但比我們夢中模糊的世界更加真實。”
愛因斯坦做出了“時空是相對的”這一成功論斷。時空本身即由物質(zhì)和能量組成。如果把所有的物質(zhì)和能量都從宇宙中拿出去,并不會剩下一個空空的容器,而是什么都沒有了。
世間存在的所有東西,都在宇宙里了。
- 集成電路制造工藝與工程應(yīng)用
- 日新月異的古代物理(上)
- Protel 99 SE實用教程(第3版)
- OLED顯示技術(shù)
- Altium Designer 16電路設(shè)計與仿真從入門到精通(清華社"視頻大講堂"大系CAD/CAM/CAE技術(shù)視頻大講堂)
- 我的第一本趣味物理書2
- 三極管應(yīng)用分析精粹:從單管放大到模擬集成電路設(shè)計(基礎(chǔ)篇)
- 反事實
- 從零開始讀懂相對論
- Altium Designer 實用教程:原理圖、PCB設(shè)計與仿真實戰(zhàn)
- 第一推動叢書·讀懂宇宙的七大經(jīng)典著作(套裝共7冊)
- 電波與光波傳輸技術(shù)
- 薛定諤講演錄
- 別萊利曼的趣味物理學(xué)
- 時空之舞:中學(xué)生能懂的相對論