- 中國財富管理發展指數
- 譚松濤
- 788字
- 2019-10-25 16:17:17
一、數據的無量綱化
(一)數量指標的無量綱化
無量綱化,也叫數據的標準化,是通過數學變換來消除原始變量(指標)量綱影響的方法。在計算單個指標指數時,首先必須對每個指標進行無量綱化處理,而進行無量綱化處理的關鍵是確定各指標的上、下限閾值。本研究中,以2013年作為“財富管理元年”,以2013年樣本城市的最大值為上限Ximax,當年底樣本城市的最小值為下限Ximin。2013年及此前后各年指標值的無量綱化處理按下述公式進行。
1.正指標的無量綱化
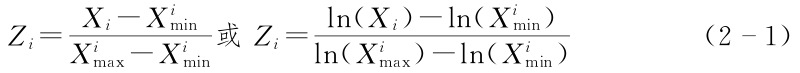
2.逆指標的無量綱化
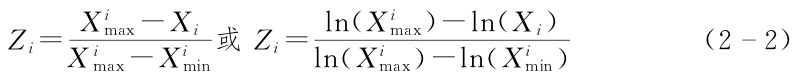
由式(2-1)和(2-2)可見,2013年的取值一定在0~1之間,而在此前后不同年份的值,既可能大于1,也可能小于0。
(二)域型指標的無量綱化
1.中間型指標的無量綱化
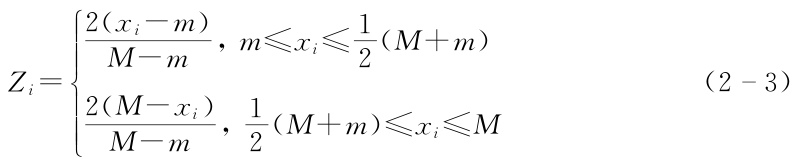
2.區間型指標的無量綱化
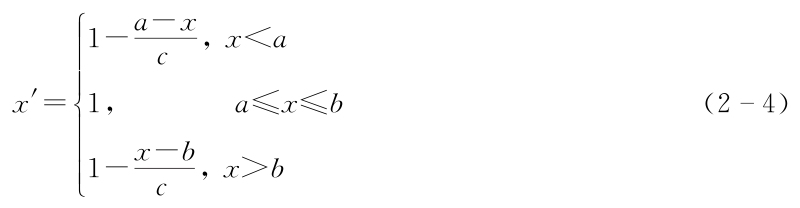
式中,[a,b]為x的最佳穩定區間,c=max{a-m,M-b},M和m分別為x可能取值的最大值和最小值。
(三)定性指標的無量綱化
有些指標直接就是定性的指標,比如群眾滿意度,1~5分的評分,雖然表現為數值,但實際是定性的;另有一些指標本身可能不是定性的,但其數值不能直接加入指標體系中進行計算,需要對其進行處理。比如某市政策性文件中對“財富管理”提及的次數,反映了對該產業的重視程度,但是其重視程度與提及次數并非線性對應關系,需要進行處理。這里處理的辦法統一設置為:
第一步,規定不同數值區域的得分,分別定為1~5分。比如文件中從未提及“財富管理”,取值為1;提及該詞1~3次,取值為2;提及3~5次,取值為3;提及5~10次,取值為4;提及10次以上,取值為5。
第二步,按下述方法對取值標準化:
取偏大型柯西分布和對數函數作為隸屬函數:
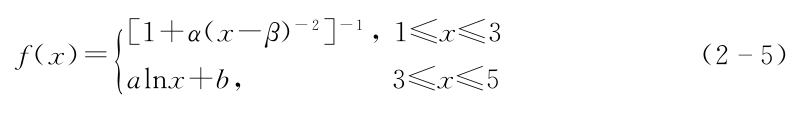
式中,α,β,a,b為待定常數。
將“政府很重視”的隸屬度定義為1,即f(5)=1;
將“政府較重視”的隸屬度定義為0.8,即f(3)=0.8;
將“政府不重視”的隸屬度定義為0.01,即f(1)=0.01。
計算得α=1.1086,β=0.8942,a=0.3915,b=0.3699。則

函數圖像見圖2-2。
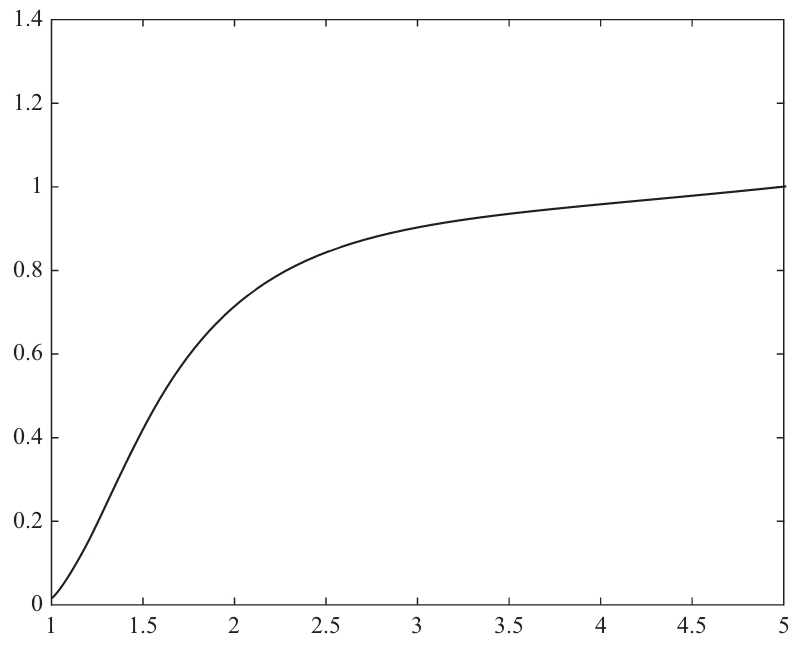
圖2-2 函數圖
根據這個規律,對于任何一個評價值,都可給出一個合適的量化值。