窺探更高的維度

研究高維度系統(tǒng)的好處之一是，可以發(fā)現(xiàn)一些無法從簡單場景里看出的模式。例如在下一章，我們將討論：在一個被巨大海洋覆蓋的球形行星上，洋流不可能在任何點都朝同一個方向流動（例如全部從西流向東）。事實上一定會發(fā)生的是：一定存在著某些點，海水是靜止不動的。雖然這條規(guī)則適用于二維曲面，但我們只有從更高維的系統(tǒng)觀察，也就是考慮水分子在曲面上所有可能運動的情況，才能導出這個規(guī)則。這是為何我們不斷向更高維度推進的原因，希望看看這樣能把我們帶到什么方向并學習到什么。

很自然的，考慮更高維度的結(jié)果之一是更大的復雜度。例如所謂“拓撲學”（Topology）是一門將物體依最廣義的形狀加以分類的學問。根據(jù)拓撲學，一維空間只有兩種：直線（或兩端無端點的曲線）和圓圈（沒有端點的封閉曲線），此外再無其他可能性。你或許會說，線也可以是彎彎曲曲的，或者封閉曲線也可能是長方形的，但這些是幾何學的問題，不屬于拓撲學的范疇。說到幾何學和拓撲學的差別，前者就像拿著放大鏡研究地球表面，而后者則像搭上太空船，從外太空觀察整個地球。選擇何者，要視底下的問題而定：你是堅持要知道所有細節(jié)，比方說地表上的每一峰脊、起伏和溝壑，抑或只要大致的全貌（“一個巨大圓球”）便已足夠？幾何學家所關(guān)切的通常是物體精確的形狀和曲率，而拓撲學家只在乎整體形貌。就這層意義而言，拓撲學是一門整體性的學問，這和數(shù)學的其他領(lǐng)域恰恰形成明顯對比，因為后者的進展，通常是借由把復雜的物件分割成較小較簡單的部分而達成。

也許你會問：這些和維度的討論有何關(guān)系？如上所述，拓撲學中只有兩種基本的一維圖形，但直線和歪歪扭扭的線是“相同”的，正圓也和任何你想象得出的“閉圈”，不論是如何彎的，多邊形、長方形，乃至于正方形都是相同的。

二維空間同樣也只有兩種基本形態(tài)：不是球面就是甜甜圈面。拓撲學家把任何沒有洞的二維曲面都視為球面，這包括常見的幾何形體，像立方體、角柱、角錐的表面，甚至形狀像西瓜的橢球面。在此，一切的差別就在于甜甜圈有洞，而球面沒有洞：無論你怎樣把球面扭曲變形（當然不包括在它中間剪洞），都不可能弄出一個甜甜圈來，反之亦然。換句話說，如果不改變物體的拓撲形態(tài)，你就無法在它上面產(chǎn)生新的洞或是撕裂它。反過來說，假如一個形體借由擠壓或拉扯，但非撕裂（假設(shè)它是由玩具黏土做成的），變成另一個形體，拓撲學家就把這兩個形體看成是相同的。

只有一個洞的甜甜圈，術(shù)語稱為“環(huán)面”（torus），但是一般甜甜圈可以有任意數(shù)目的洞。“緊致”（compact，封閉且范圍有限）且“可賦向”（orientable，有內(nèi)外兩面）的二維曲面可以依洞的數(shù)目來分類，這個數(shù)目稱為“虧格”（genus）。外觀回異的二維物體，如果虧格相同，在拓撲上被視為是相同的。

先前提到二維形體只有球面與洞數(shù)不同的甜甜圈面兩大類，這只有在可賦向曲面的情況才成立，本書所討論的通常都是可賦向曲面。比方說，海灘球有兩個面，即里面和外面，輪胎的內(nèi)胎也有兩個面。然而，對于比較復雜的情況，例如單面或“不可賦向”的曲面如“克萊因瓶”（Klein bottle）和“莫比烏斯帶”（M?bius strip），上述說法并不成立。

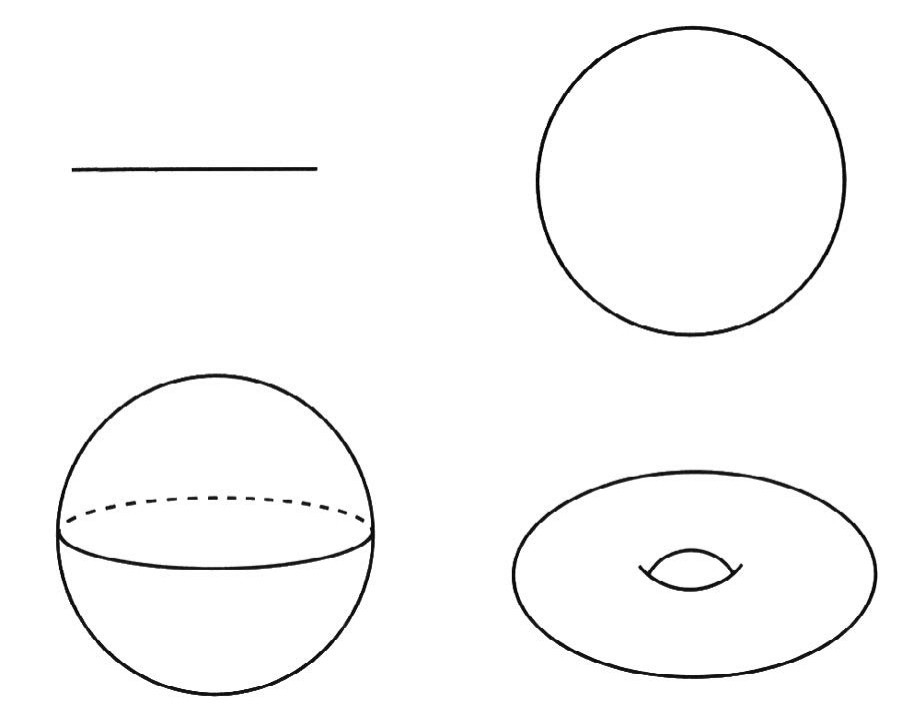
圖1.1 在拓撲學中，一維的空間只有兩種：線與圓，兩者有著根本的不同，你可以把圓轉(zhuǎn)變成各式各樣的閉圈，但是不能變成線，除非你將它剪開。

可賦向的二維空間像海灘球，有里外兩個面，不像莫比烏斯帶只有一個面。可賦向二維空間可以用虧格來區(qū)分，虧格可以簡單想成洞的數(shù)目。例如，球面沒有洞，虧格是0；普通甜甜圈（環(huán)面）有一個洞，虧格是1；兩者有根本的不同。如同線和圖的情況一樣，不在球面上開個洞，是不可能將球面轉(zhuǎn)變成甜甜圈的

如果是三維以上，可能的形體數(shù)就會急劇增加。當考慮高維空間時，必須容許我們往難以想象的方向移動。在此所指的可不是介于向北和向西之間的西北方，或是“北西北”的這類方向，而是完全跑出三維網(wǎng)格之外，這個方向落在一個我們還沒畫出的坐標系里面。

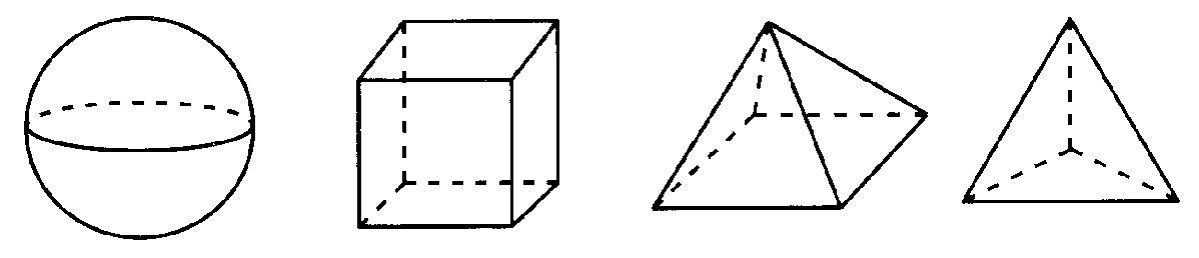
圖1.2 在拓撲學中，球、正方體、四角錐（金字塔）、正四面體的表面被認為是等價的，因為只要通過彎曲、伸展、壓縮，它們就可以互相轉(zhuǎn)換，并不需要撕裂或剪開。

圖1.3 虧格為0、1、2、3（從左到石）的曲面，虧格指的是其中的洞數(shù)