1.4 計算機數(shù)的運算基礎

1.4.1 進位計數(shù)制及相互轉換

1.進位計數(shù)制

按進位的原則進行計數(shù)的方法稱為進位計數(shù)制，簡稱進位制。人們在日常生活中習慣使用十進制，但二進制易于實現(xiàn)、存儲、傳輸，所以計算機中采用二進制。而二進制不易于書寫和閱讀，因此又引入了八進制和十六進制。

1）十進制（后綴或下標D表示）

十進制計數(shù)原則：逢十進一

十進制的基數(shù)：10

十進制的數(shù)碼：0 1 2 3 4 5 6 7 8 9

十進制數(shù)第K位的權：10K

第K位的權為基數(shù)的K次方，第K位的數(shù)碼與第K位權的乘積表示第K位數(shù)的值。

例如：8846.78D=8×103+8×102+4×101+6×100+7×10-1+8×10-2。

該數(shù)中共出現(xiàn)三次數(shù)碼8，但各自的權不一樣，故其代表的值也不一樣。

2）二進制（后綴或下標B表示）

二進制計數(shù)原則：逢二進一

二進制的基數(shù)：2

二進制的數(shù)碼：0 1

二進制數(shù)第K位的權：2K

例如：11010101.01B=1×27+1×26+0×25+1×24+0×23+1×22+0×21+1×20+0×2-1+1×2-2=213.25D。

N位二進制數(shù)可以表示2N個數(shù)。例如，3位二進制數(shù)可以表示8個數(shù)，如表1.3所示。

3）八進制（后綴或下標O表示）

八進制計數(shù)原則：逢八進一

八進制的基數(shù)：8

八進制的數(shù)碼：0 1 2 3 4 5 6 7

八進制數(shù)第K位的權：8K

例如：127O=1×82+2×81+7×80=87D。

4）十六進制（后綴或下標H表示）

十六進制計數(shù)原則：逢十六進一

十六進制的基數(shù)：16

十六進制的數(shù)碼：0 1 2 3 4 5 6 7 8 9 A B C D E F

十六進制數(shù)第K位的權：16K

例如：64.4H=6×161+4×160+4×16-1=100.25D。

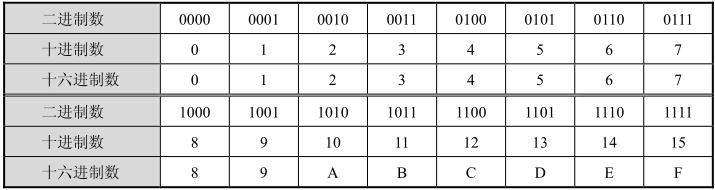
十六進制數(shù)、二進制數(shù)和十進制數(shù)的對應關系如表1.4所示。

2.不同進制數(shù)之間的轉換

1）二進制數(shù)轉換為十進制數(shù)

轉換原則：按權展開求和。

例如：10001101.11B=1×27+0×26+0×25+0×24+1×23+1×22+0×21+1×20+1×2-1+1×2-2=141.75D。

八進制數(shù)和十六進制數(shù)轉換為十進制數(shù)也同樣遵循該原則，不再單獨介紹。

2）十進制數(shù)轉換為二進制數(shù)

十進制數(shù)轉換為二進制數(shù)的原則：① 整數(shù)部分除基取余，逆序排列；

　　　　　　　　　　　　　　　② 小數(shù)部分乘基取整，順序排列。

例如：將十進制數(shù)186和0.8125轉換成二進制數(shù)。

所以：186D=10111010B，0.8125D=0.1101B。

十進制數(shù)轉換為八進制數(shù)和十六進制數(shù)同樣遵循該原則。

3）二進制數(shù)轉換為十六進制數(shù)

由于十六進制的基數(shù)是2的冪，所以二進制數(shù)與十六進制數(shù)之間的轉換是十分方便的。二進制數(shù)轉換為十六進制數(shù)的原則：整數(shù)部分從低位到高位4位一組（不足補零），直接用十六進制數(shù)來表示；小數(shù)部分從高位到低位4位一組（不足補零），直接用十六進制數(shù)表示。

例如：將二進制數(shù)10011110.00111轉換成十六進制數(shù)。

所以：10011110.00111B=9E.38H。

4）十六進制數(shù)轉換為二進制數(shù)

十六進制數(shù)轉換為二進制數(shù)的原則：十六進制數(shù)中的每一位用4位二進制數(shù)來表示。

例如：將十六進制數(shù)A87.B8轉換為二進制數(shù)。

所以：A87.B8H=101010000111.10111000B。

八進制的基數(shù)同樣是2的冪，因此二進制數(shù)與十六進制數(shù)之間的轉換也遵循以上的原則，只是將原則中的4位改成3位。

例如：將二進制數(shù)11010110.110101轉換成八進制數(shù)。

將八進制數(shù)746.42轉換成二進制數(shù)。

所以：11010110.110101B=326.65O，746.42O=111100110.100010B。

3.八進制數(shù)和十六進制數(shù)運算

1）二進制數(shù)的運算

加法法則 乘法法則

0+0=0 0×0=0

0+1=1 0×1=0

1+0=1 1×0=0

1+1=0（進位1） 1×1=1

2）十六進制數(shù)的運算

十六進制數(shù)的運算遵循“逢十六進一”的原則。

（1）十六進制數(shù)加法。

十六進制數(shù)相加，當某一位上的數(shù)碼之和S＜16時與十進制數(shù)進行同樣處理。如果數(shù)碼之和S≥16時，則應該用S減16及進位1來取代S。

例如：

（2）十六進制數(shù)減法。

十六進制數(shù)減法也與十進制數(shù)類似，夠減時直接相減，不夠減時服從向高位借1為16的原則。

例如：

十六進制數(shù)的乘除運算同樣根據(jù)“逢十六進一”的原則處理，這里不再詳述。

1.4.2 計算機中數(shù)和字符的表示

1.計算機中有符號數(shù)的表示

計算機中的數(shù)是用二進制來表示的，有符號數(shù)中的符號也是用二進制數(shù)值來表示。0表示“+”號，1表示“-”號，這種符號數(shù)值化之后表示的數(shù)稱為機器數(shù)，它表示的數(shù)值稱為機器數(shù)的真值。

為將減法變?yōu)榧臃ǎ苑奖氵\算簡化CPU的硬件結構，機器數(shù)有三種表示方法：原碼、反碼和補碼。

1）原碼

最高位為符號位，符號位后表示該數(shù)的絕對值。例如：

[+112]原=01110000B；

[-112]原=11110000B。

其中最高位為符號位，后面的7位是數(shù)值（字長為8位；若字長為16位，則后面15位為數(shù)值）。

用原碼表示時，+112和-112的數(shù)值位相同，符號位不同。

說明：

（1）0的原碼有兩種表示法。

[+0]原=00000000B；

[-0]原=10000000B。

（2）N位原碼的表示范圍為1-2N-1～2N-1-1。

例如：8位原碼表示的范圍為-127～+127。

2）反碼

最高位為符號位，正數(shù)的反碼與原碼相同；負數(shù)的反碼為其正數(shù)原碼按位求反。例如：

[+112]反=01110000B；

[-112]反=10001111B。

說明：

（1）0的反碼有兩種表示法。

[+0]反=00000000B；

[-0]反=11111111B。

（2）N位反碼表示的范圍為1-2N-1～2N-1-1。

例如：8位反碼表示的范圍為-127～+127。

（3）符號位為1時，其后不是該數(shù)的絕對值。

例如：反碼11100101B的真值為-27，而不是–101。

3）補碼

最高位為符號位，正數(shù)的補碼與原碼相同；負數(shù)的補碼為其正數(shù)原碼按位求反再加1。例如：

[+112]補=01110000B；

[-112]補=10010000B。

說明：

（1）0的補碼只有一種表示法：[+0]補=[-0]補=00000000B。

（2）N位補碼所能表示的范圍為-2N-1～2N-1-1。

例如：8位補碼表示的范圍為-128～+127。

（3）8位機器數(shù)中：[-128]補=10000000B，[-128]原和[-128]反不存在。

（4）符號位為1時，其后不是該數(shù)的絕對值。

例如：補碼11110010B的真值為-14，而不是-114。

有符號數(shù)采用補碼表示時，就可以將減法運算轉換為加法運算。因此計算機中有符號數(shù)均以補碼表示。

例如：X=84-16=（+84）+（-16）→[X]補=[+84]補+[-16]補。

[+84]補=01010100B。

[-16]補=11110000B。

所以：[X]補=01000100B，即X=68。

在字長為8位的機器中，第7位的進位自動丟失，但這不會影響運算結果。機器中這一位并不是真正丟失，而是保存在程序狀態(tài)字PSW中的進位標志Cy中。

又如：X=48-88=（+48）+（-88）→[X]補=[+48]補+[-88]補。

[+48]補=00110000B。

[-88]補=10101000B。

所以：[X]補=11011000B，即X=-40。

為進一步說明補碼如何將減法運算轉換為加法運算，我們舉一個日常的例子：對于鐘表，它所能表示的最大數(shù)為12點，我們把它稱之為模，即一個系統(tǒng)的量程或所能表示的最大的數(shù)。若當前標準時間為6點，現(xiàn)有一只表為9點，可以有兩種調時方法。

① 9-3=6（倒撥）。

② 9+9=6（順撥）。

即有9+9=9+3+6=12+6=9-3。

因此對某一確定的模，某數(shù)減去小于模的一數(shù)，總可以用加上該數(shù)的負數(shù)與其模之和（即補碼）來代替。故引入補碼后，減法就可以轉換為加法。

補碼表示的數(shù)還具有以下特性。

[X+Y]補=[X]補+[Y]補

[X-Y]補=[X]補+[-Y]補

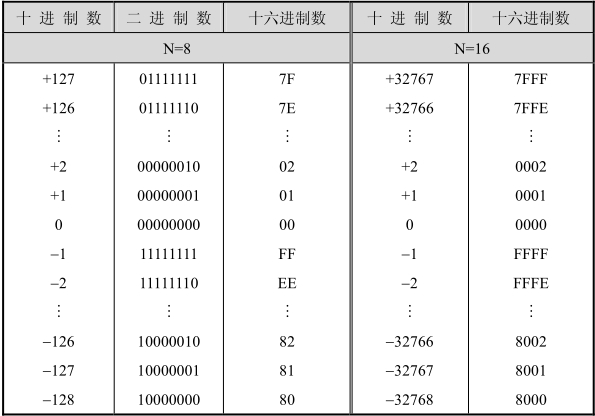
如表1.5所示為N=8和N=16時N位補碼數(shù)的表示范圍。

2.無符號整數(shù)

在某些情況下，處理的全是正數(shù)時，就不必再保留符號位。我們把最高有效位也作為數(shù)值處理，這樣的數(shù)稱之為無符號整數(shù)。8位無符號數(shù)表示的范圍為0～255。

計算機中最常用的無符號整數(shù)是表示存儲單元地址的數(shù)。

3.字符表示

字母、數(shù)字、符號等各種字符（例如，鍵盤輸出的信息或打印輸出的信息都是按字符方式輸出）按特定的規(guī)則，用二進制編碼在計算機中表示。字符的編碼方式很多，最普遍采用的是美國標準信息交換碼ASCII碼。

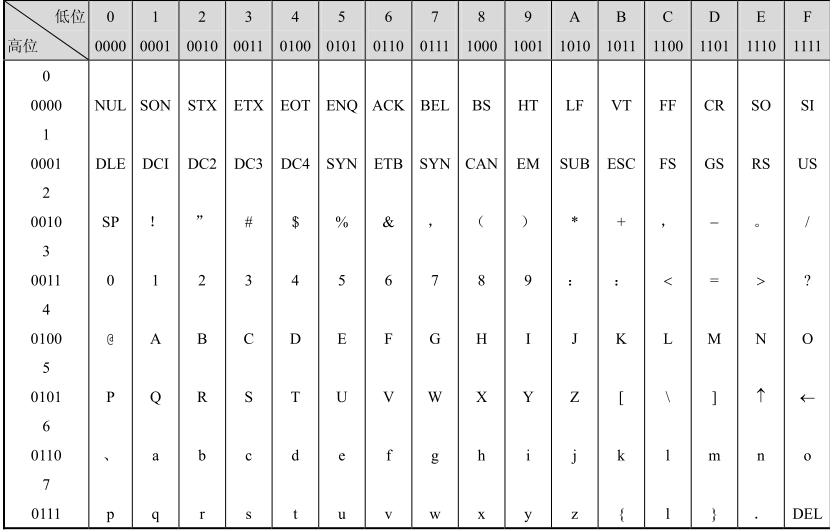
ASCII碼是7位二進制編碼。計算機中用一個字節(jié)表示一個ASCII碼字符，最高位默認為0，可用做校驗位，如表1.6所示。

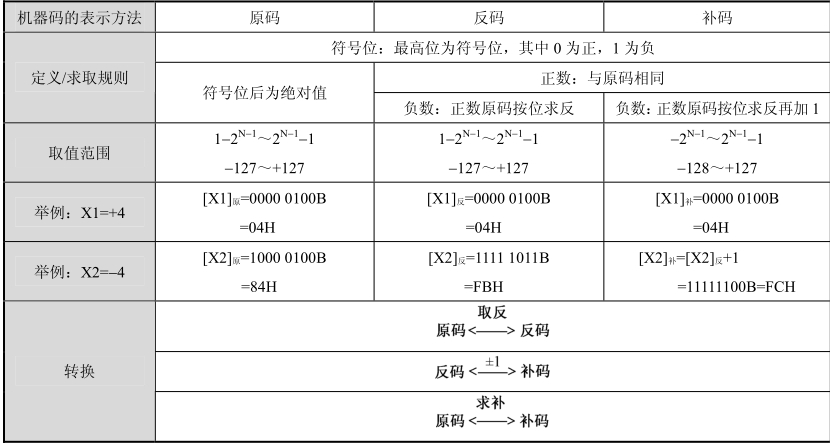
相關機器碼間關系如表1.7所示。