1.15 技術證明*

定理1.1 證明 令ω∈A.由于{B1, B2,···}是S的一個分割，則存在i使得ω∈Bi.令Ai=（A∩Bi），則即每個A中的元素都在中.

現在令，則存在i使得ω∈Ai.這表明w∈A，即每個中的元素都在Ai中.

因為Bi是互不相交的，對i≠j，Ai∩Aj=（A∩Bi）∩（A∩Bj）=A∩（Bi∩Bj）=?.因此，Ai是互不相交的.

■

定理1.2 性質1證明A和Ac是不相交的，且A∪Ac=S.利用概率公理第二條和第三條得

移項得，P[Ac]=1-P[A].

■

定理1.2 性質2證明 我們有?=Sc.由定理1.2和概率公理的第二條得P[?]=1-P[S]=0.

■

定理1.2 性質3證明由概率公理的第一條得P[Ac]≥0.由式（1.1）得

P[A]=1-P[Ac]≤1

■

定理1.2 性質4證明由假設A?B得A∩B=A.由分割定理（定理1.1）得B=（B∩A）∪（B∩Ac），其中A和B∩Ac是不相交的.由概率公理的第三條得

P[B]=P[A]+P[B∩Ac]≥P[A]

其中，由概率公理的第一條得P[B∩Ac]≥0.因此，P[B]≥P[A].

■

定理1.2 性質5證明 我們有{A∪B}=A∪{B∩Ac}，其中A和{B∩Ac}是不相交的.同樣有B={B∩A}∪{B∩Ac}，其中{B∩A}和{B∩Ac}是不相交的.由這兩個關系和概率公理的第三條得

P[A∪B]=P[A]+P[B∩Ac]

P[B]=P[B∩A]+P[B∩Ac]

兩式相減，

P[A∪B]-P[B]=P[A]-P[B∩A]

移項得所求結果.

■

定理1.2 性質6證明由容斥原則和P[A∩B]≥0（概率公理的第一條）得

P[A∪B]=P[A]+P[B]-P[A∩B]≤P[A]+P[B]

■

定理1.2 性質7證明由移項后的容斥原則和P[A∩B]≤1（概率公理的第三條）得

P[A∩B]=P[A]+P[B]-P[A∪B]≥P[A]+P[B]-1

則結果成立.

■

定理1.11 證明 （二項式定理）乘法展開后，

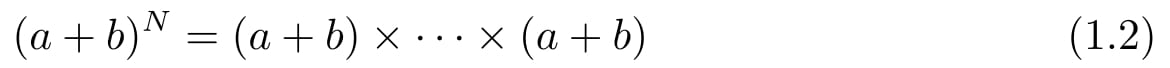
是a和b的多項式，共有2N項.每一項都是K個a和N-K個b的乘積，因此可寫為aKbN-K.項的總數等于從N個a中選出K個a的組合數.因此，式（1.2）等于.

■