“再一次，一再重復(fù)”——建立關(guān)系法

在讀一本關(guān)于邏輯思考中的錯(cuò)誤的書時(shí)，我了解到描述增長率的百分?jǐn)?shù)往往會(huì)被低估。比如：狗的數(shù)量每年增加5%。這聽起來沒什么了不起的。但是，如果這件事說的是多少年后狗的數(shù)目會(huì)翻倍，明顯會(huì)令人印象更加深刻。為了計(jì)算這個(gè)年數(shù)，我們在此可以使用一個(gè)“經(jīng)驗(yàn)法則”：用數(shù)字70除以百分比中的數(shù)字，得到的便是一個(gè)數(shù)量翻一倍所需要的年數(shù)。所以這個(gè)例子中為70÷5 =14——14年后狗的數(shù)量將是今天的兩倍！

可是最初我很困惑：因?yàn)槲也涣私狻?0規(guī)則”(8)，數(shù)字70與數(shù)量翻一番有什么關(guān)系呢？一眼看去并不相關(guān)。我用不同的百分比數(shù)值仔仔細(xì)細(xì)地算了幾遍，竟然真的可以確定，這條規(guī)則是完全可以使用的——至少在百分比數(shù)值比較低的情況下。我在互聯(lián)網(wǎng)上找到了這條源自復(fù)利公式的規(guī)則推導(dǎo)。我們在進(jìn)行大致的快速估算時(shí)，這樣一條經(jīng)驗(yàn)法則是相當(dāng)好用的。

但是，如果想知道一個(gè)數(shù)值擴(kuò)大為三倍需要多久，又該怎么辦呢？這時(shí)使用“70規(guī)則”就沒有效果了，因?yàn)槲覀冎涣私馍厦嫣峒暗奶厥馇闆r。

我們在學(xué)校里學(xué)習(xí)了大量類似的特殊規(guī)則、公式或概念。我們像一臺(tái)復(fù)印機(jī)一樣記錄下這些內(nèi)容，并在需要時(shí)盡可能按照原樣輸出它們而并不理解背后隱藏的意義到底是什么。填鴨式教育成了當(dāng)務(wù)之急：吞下知識(shí)，在要求提取時(shí)“吐出”（甚至可以因此而變得出類拔萃）之后便清空。雖然我們能夠以此方法取得高分，但并不能解決現(xiàn)實(shí)中的問題。

自然，沒有人能不通過背誦和重復(fù)而有效學(xué)習(xí)。但如果我們能夠建立起關(guān)系，將所學(xué)之物嵌入具體情境及已有的知識(shí)體系，那么學(xué)習(xí)就會(huì)更有效和持久。例如，如果我們要記住數(shù)字1492，可能很多人會(huì)立即想到這是發(fā)現(xiàn)美洲大陸的年份；面對數(shù)字1003，歌劇迷則會(huì)馬上想到唐璜(9)（因?yàn)樗麅H在西班牙就誘惑了這么多女人）；數(shù)學(xué)愛好者在3.14這個(gè)數(shù)字上看到的是圓周率，等等。由于我們不能立刻就為所有事物建立起合適的聯(lián)系，各式各樣的學(xué)習(xí)指導(dǎo)或記憶訓(xùn)練大師便推薦大家通過編造故事的方法刻意建立人為的聯(lián)系。物理學(xué)家見到這類建議會(huì)急得直拍腦袋，因?yàn)槿绻菫榱私鉀Q問題而追求知識(shí)，就應(yīng)該把這些方法統(tǒng)統(tǒng)忘掉！只有展示出所需理解之事背后的規(guī)律性或真實(shí)因果關(guān)系的思維關(guān)聯(lián)才是有用的，才真正奏效。

對很多人來說，這需要的時(shí)間太長。在我們建立思維關(guān)聯(lián)之前，一個(gè)小蜜蜂似的勤奮學(xué)習(xí)者已經(jīng)可以背下一個(gè)句子、一個(gè)數(shù)字或一種解決方案。短期看來，記憶學(xué)習(xí)者和復(fù)制者好像更占優(yōu)勢。但是，看得更深刻的人可以從關(guān)聯(lián)中推導(dǎo)出原因，或在很多其他事物上應(yīng)用自己的認(rèn)識(shí)。例如，如果我們真正掌握了所謂的“交叉相乘法”(10)，很多比例或利息計(jì)算、理工科的特殊公式與概念便不需要死記硬背，因?yàn)楹苋菀拙湍芡茖?dǎo)出來。通過這樣的方法，學(xué)校里的各種“公式大合集”是可以廢除的——在學(xué)生學(xué)會(huì)獨(dú)立思考的前提下。但不幸的是，現(xiàn)在的發(fā)展趨勢恰恰相反：由于時(shí)間緊缺，我們尚未理解公式便去應(yīng)用，于是常有愚蠢的結(jié)果隨之而來。

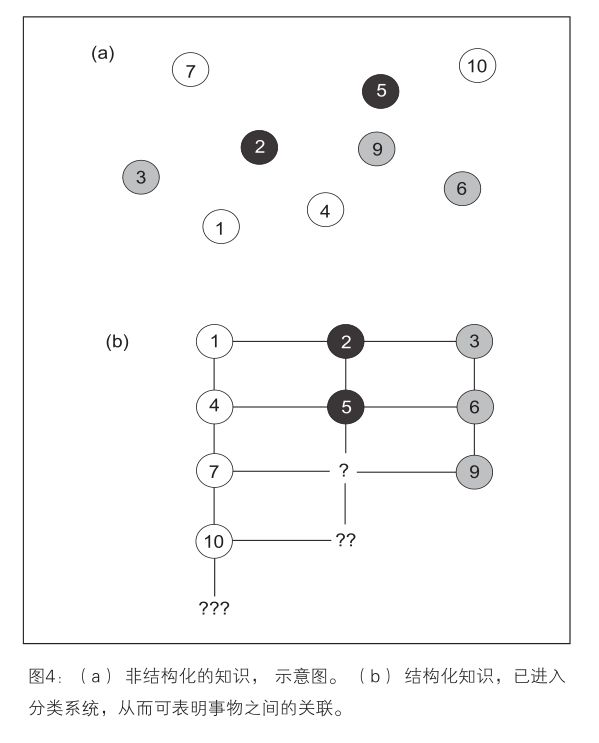
圖4展示了識(shí)別事物之間關(guān)系的優(yōu)勢。在圖4（a）情境下，我們一眼看去只能認(rèn)出幾個(gè)寫著數(shù)字的小球。從廣義上說：如果孤立看待現(xiàn)象、事實(shí)、事件，往往只能看到一片混亂，只能費(fèi)力設(shè)法應(yīng)對。在圖4（b）情境下則不同，小球在這里是根據(jù)數(shù)值和顏色整理排列的，一目了然，我們能看到缺少了什么或應(yīng)該補(bǔ)充什么，而且非常重要的是：如果布局順序被打亂或忘記了原來存在哪些小球，我們可以重建混亂或遺忘過程中丟失的信息！此外，新出現(xiàn)的現(xiàn)象不會(huì)令我們驚訝，因?yàn)楸匾獣r(shí)它們也能被納入體系。我們有時(shí)甚至還可以預(yù)測迄今缺席并可使體系完整的事物。在圖4（b）所示的體系中，尚缺失的應(yīng)是寫著白色數(shù)字8的黑色小球。

概括性、結(jié)構(gòu)化、網(wǎng)絡(luò)化的知識(shí)可以加倍地發(fā)揮效用，而填鴨式學(xué)習(xí)者在問題或任務(wù)設(shè)置發(fā)生微小改變時(shí)，也極可能失敗，因?yàn)樗麄冊诿恳淮蚊鎸π率挛飼r(shí)不得不從頭再來。所以面臨與日俱增的信息洪流，如果不學(xué)會(huì)將知識(shí)結(jié)構(gòu)化，我們將遭遇越來越多的困難。

當(dāng)然，世上不僅僅存在容易辨認(rèn)的關(guān)系。很多事物我們最初只能毫無關(guān)聯(lián)地接受和感知。只有發(fā)現(xiàn)構(gòu)建、組合一切的“規(guī)劃圖紙”的基本原則時(shí)，我們才可能理解復(fù)雜的事物。真正認(rèn)識(shí)、理解的知識(shí)，往往可以重復(fù)利用或至少能夠在略加改變和調(diào)整后應(yīng)用。物理學(xué)家通過這種方法節(jié)省了大量的時(shí)間與精力。但問題是：我們該如何發(fā)現(xiàn)可以幫助我們保持全局觀的關(guān)系、關(guān)聯(lián)呢？

練習(xí)

練習(xí)10：嘗試辨認(rèn)、找出各組成部分之間的關(guān)系，從而在所有混亂中都找到秩序。

練習(xí)11：面對任何情況都試著自問，哪些因果規(guī)律使事物成為其現(xiàn)在的狀態(tài)，而不是另外的狀態(tài)。