1.5　元分析

是否有定量分析表明表1-1中的所有差異都可能源于抽樣誤差？假定我們按樣本量對每個相關(guān)性進行加權(quán)平均以計算其方差，得到的值是0.022 58（SD=0.150）。我們也可以僅僅根據(jù)抽樣誤差計算期望方差。每個獨立相關(guān)性ri的抽樣誤差方差公式為：

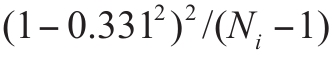
其中，0.331是表1-1中相關(guān)性的樣本加權(quán)均值。如果我們按照樣本量對每個估計值進行加權(quán)（就像我們在計算觀察方差時所做的那樣），那么抽樣誤差期望方差公式是：

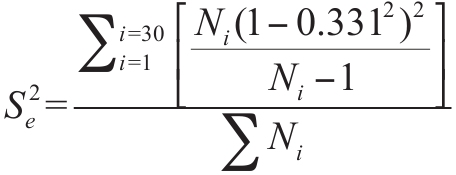
該值為0.020 58（SD=0.144）。抽樣誤差期望方差與實際（觀察）方差之比為0.020 58/0.022 58=0.91。因此，僅抽樣誤差就占了相關(guān)關(guān)系中觀察方差的91%。0.91的平方根是抽樣誤差和觀察的相關(guān)性之間的相關(guān)性。該相關(guān)性為0.95，是一個比方差百分比更具信息量的指標（Schmidt，2010）。最好的結(jié)論是，工作滿意度和組織承諾之間的關(guān)系在性別、種族、工作層次、年齡、地理位置和組織規(guī)模上是恒定的（相關(guān)性1.00和我們的0.95之間的差異是由二階抽樣誤差引起的，這在第9章有討論）。這個常數(shù)值的最佳估計是0.331，即30個相關(guān)性樣本量加權(quán)的均值。在我們的口頭報告中，研究者對這30項研究的數(shù)據(jù)進行了定性分析，不同的人得出了不同的結(jié)論。相比之下，所有使用這個定量方法的研究者都會（剔除計算誤差）得出完全相同的結(jié)論。

從理論上講，0.331不是我們想要的值，因為這兩個量表的不可靠性都會使它向下偏差。測量誤差的影響減少所有觀察的相關(guān)性，從而使平均相關(guān)性低于兩個構(gòu)念之間的實際相關(guān)性。我們感興趣的是構(gòu)念層面的相關(guān)性，因為這種相關(guān)性反映了潛在的科學性。假設根據(jù)30項研究的資料，我們估計工作滿意度的平均信度為0.70，組織承諾的平均信度為0.60。進一步，這些被估計的量表真實分數(shù)的相關(guān)性是。這個值是構(gòu)念層面相關(guān)性的最佳估計。Schmidt、Le、Oh（在版中）已經(jīng)表明，真實分數(shù)和構(gòu)念分數(shù)之間的相關(guān)性通常達到0.98。因此真實分數(shù)相關(guān)性是對構(gòu)念相關(guān)性的良好估計。Hedges討論了校正測量誤差的必要性（2009b，第3章）。

除抽樣誤差之外，大多數(shù)扭曲研究結(jié)果的人為誤差都是系統(tǒng)的，而不是隨機的。它們通常使r值或d值產(chǎn)生向下偏差。例如，研究中的所有變量必須測量，并且所有變量測量值都包含測量誤差。這條規(guī)則是毫無例外的。測量誤差影響每個相關(guān)值或d值向下偏差。測量誤差也可能導致研究間的差異：如果一項研究中測量的誤差比另一項研究中測量的誤差更大，則在第一項研究中觀察的rs或ds將更小。因此，元分析必須校正向下偏差以及不同研究間人為誤差的差異。這種校正在第2章到第7章中進行討論。

傳統(tǒng)的文獻綜述方法不足以整合大量研究中相互矛盾的結(jié)果。正如Glass（1976）指出的那樣，數(shù)百項研究的結(jié)果：“在傳統(tǒng)的描述性文獻綜述中，如果沒有在組織、描繪和解釋數(shù)據(jù)的技巧幫助下，就無法理解500個考試成績的意義”（p.4）。在班級規(guī)模對學生學習的影響，智商與創(chuàng)造力的關(guān)系以及心理治療對患者的影響等領域，短期內(nèi)幾乎可以積累成百上千的研究。Glass（1976）指出，這些研究總體上包含的信息比用描述性綜述方法所提取的信息要多得多。他指出，因為我們沒有開發(fā)這些信息“金礦”，所以“我們知道的比我們已經(jīng)證實的要少得多”。我們需要的是綜合現(xiàn)有研究結(jié)果的方法，以揭示相對不變的潛在關(guān)系和因果關(guān)系模式，它的建立將構(gòu)成一般原則和累積的知識。

在心理學和社會科學史上，迫切需要更多的實證研究來檢驗這個問題。在許多研究領域，今天的需求不是額外的實證數(shù)據(jù)，而是了解一些已累積大量數(shù)據(jù)的方法。由于心理學和其他社會科學領域的數(shù)量越來越多，可用的研究的數(shù)量巨大，因此為了將相互矛盾的研究結(jié)果整合起來以建立普適的知識，促進理論開發(fā)和實際問題的解決顯得尤為重要，這使得元分析在研究中發(fā)揮著越來越重要的作用。這些方法可以建立在我們已經(jīng)熟悉的統(tǒng)計和心理測量方法的基礎上。正如Glass（1976）所說：

在對研究數(shù)據(jù)進行初步分析時，我們大多數(shù)人都受過分析變量之間復雜關(guān)系的訓練。但在更高層次上，方差、非同質(zhì)性和不確定性同樣明顯，我們常常用文字描述取代量化的嚴謹性。正確的整合研究需要采用與原始數(shù)據(jù)分析相同的統(tǒng)計方法。（p.6）