2.1.1 馬爾可夫決策過程和回溯圖

在第1章中，已經簡單介紹了強化學習的基本原理，這里簡單回顧一下這些概念，并且進行深入闡述。首先是馬爾可夫決策過程（Markov Decision Process, MDP）。這個決策過程基于以下原理：智能體的決策過程僅和其當前所處的狀態有關，與智能體所經歷的歷史無關。在這種理想的狀態下，智能體所處的每個狀態都是有其價值的，可以定義對應的狀態價值函數V_π（s_t），注意到這個狀態價值函數除了和當前時刻的狀態s_t有關，還和我們采取的策略π有關。當然，這個狀態函數是智能體在策略π的條件下，每個狀態按照一定的概率采取不同的動作a_t得到的最終價值的期望，我們可以把狀態價值函數進一步細化，得到對應的狀態-動作價值函數Q_π（s_t，a_t）。于是在這個條件下，給每個對應的狀態動作的組合對（s_t，a_t）計算對應的價值，整個強化學習模型的決策可以根據對應的組合對的值得到。由于馬爾可夫的決策過程之間的狀態具有固定的依賴關系，即當前的狀態僅依賴于上一步的狀態，這里可以使用回溯圖（Backup Diagram）的數據結構來對決策過程進行描述。一個簡單的回溯圖如圖2.1所示。

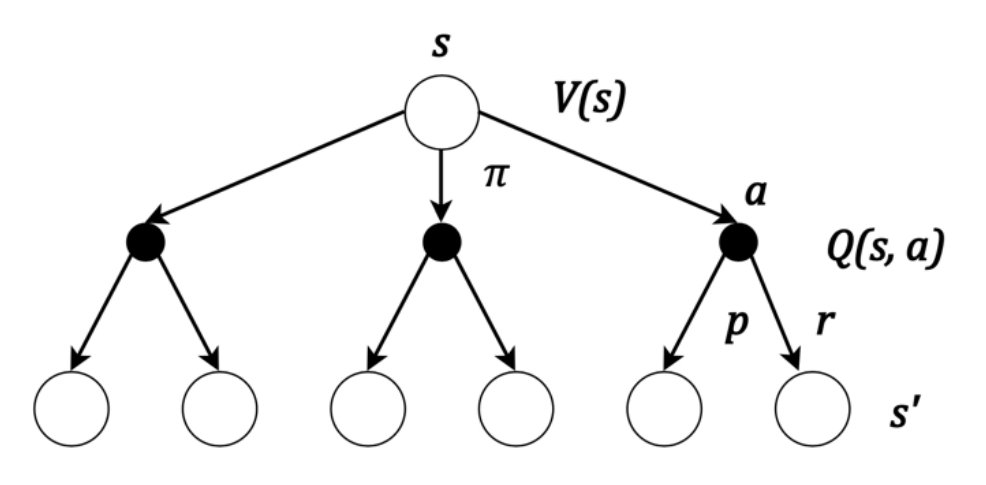
圖2.1 簡單的回溯圖示例

在圖2.1中，使用空心的圓形來代表某個狀態s，用實心的圓形來代表智能體采取的某個動作a，箭頭的鏈接代表狀態和動作之間的因果關系。在這個圖中可以看到，如果從初始狀態s出發，根據策略π采取一個動作a，有一定的概率p，可以到達一個新的狀態s′，同時獲取獎勵r。反之，根據這個回溯圖可以找到狀態s′是由狀態s通過動作a得來的，這就是這個圖被稱為回溯圖的原因。這樣，從圖2.1的回溯圖可以直接看出，從初始狀態出發，根據策略有三種可能的動作，同時每個動作有一定的概率能夠各自到達兩個新的狀態。另外需要注意的是，回溯圖不保證狀態s和狀態s′不同，有可能經過一次決策之后狀態s回到自身。

在回溯圖所描述的決策過程中，假如已知狀態價值函數V_π（s_t）或者狀態-動作價值函數Q_π（s_t，a_t），可以很容易地根據這兩個函數的定義，得到相應的遞歸關系，如式（2.1）和式（2.2）所示。

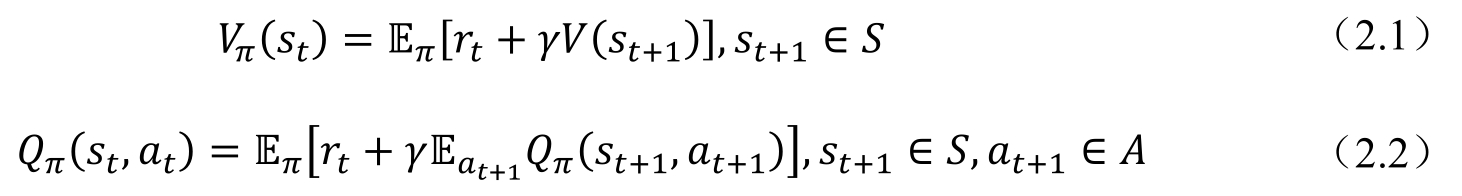
其中，s_t+1∈S代表s_t+1在所有s_t可能轉移到的狀態空間S中的取值；同樣，a_t+1∈A代表a_t+1在所有的a_t可能轉移到的狀態空間A中的取值，E_π的具體含義是在策略π下面的期望，具體的形式如式（2.3）所示。

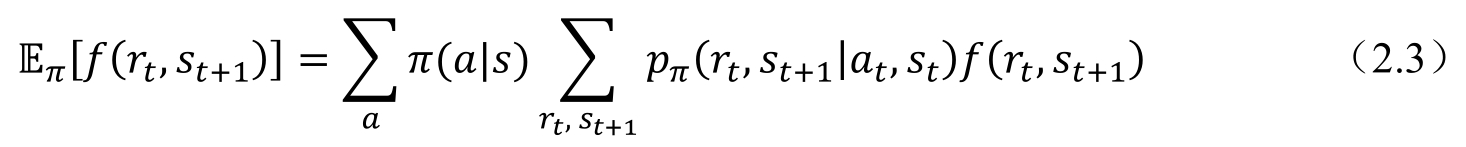
其中，p（r_t，s_t+1|a_t，s_t）為在狀態s_t下，智能體采取動作a_t，轉移到狀態s_t+1，并且獲取r_t的獎勵的概率。

在圖2.1中，對應的是從某一個狀態s_t出發，到達所有可能的其他狀態的相關聯的函數f（r_t，s_t+1）按照概率的求和（這里使用的是任意函數，讀者不難把式（2.3）應用于式（2.1）中的狀態價值函數和式（2.2）中的狀態-動作價值函數。注意，如果是狀態-動作價值函數，則不需要考慮式（2.3）中第一個關于策略概率的求和，因為在狀態-動作價值函數中動作是一個變量）。式（2.1）和式（2.2）成立的原因在于，在馬爾可夫決策過程中，相應的策略π，狀態價值函數V_π（s_t）和狀態-動作價值函數Q_π（s_t，a_t）與決策的歷史無關（參見1.2.2節的內容），也即是僅和當前所處的狀態s_t有關。這就給我們的遞歸計算過程提供了理論基礎。接下來看一下基于式（2.1）和式（2.2）最簡單的情況，即所謂最優策略下的情形。