- 聯邦學習原理與應用(全彩版)
- 向小佳等
- 3096字
- 2022-05-06 18:47:17
3.1.2 縱向聯邦學習中的線性模型
在縱向聯邦學習系統中,具有不同數據結構的參與方A和B想要合作訓練一個模型。其中,只有B方有標簽。由于隱私保護的需求和解決方法的需要,A方和B方不會直接傳輸數據,而是為了保證傳輸中數據的安全性加入了第三方C。這里,我們假設C方是誠實的且不會與A方或B方串通,為了保證C方合理且可信,可以讓官方機構承擔,或者用安全計算節點來替代。整個系統通常分為以下兩個部分。
(1)實體對齊。由于兩個參與方的樣本不一致,聯邦系統會使用基于加密的樣本id對齊技術在不暴露參與方各自數據的前提下確定公共的樣本。在這個過程中,不會泄露不重合的樣本。
(2)模型訓練。在公共的樣本確定后,基于這些樣本訓練模型。訓練步驟如下。
①第三方C生成密鑰對,把公鑰分別發送給A方和B方。
②A方和B方對中間值進行加密傳輸,完成梯度和損失的更新計算。
③A方和B方更新各自加密的梯度,B方還要完成加密損失的計算。然后,A方和B方將加密的值發送給C方。
④C方對接收的值解密,并將解密后的損失和梯度返還給A方和B方。A方和B方對模型參數進行更新。
下面分別以邏輯回歸、線性回歸和泊松回歸為例,對上述過程進行闡述。
縱向聯邦邏輯回歸:文獻[45]提出了一種基于隱私保護和信息安全的縱向聯邦邏輯回歸模型,通過對損失和梯度公式運用泰勒展開使Paillier半同態加密算法能適用于隱私保護計算。該算法支持加法運算和標量乘法運算,即對于任意明文![]() 和
和![]() ,有
,有
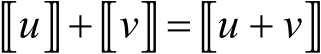
(3-1-8)
還有標量乘法公式,![]() 表示密文
表示密文![]() 的個數,即
的個數,即
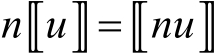
(3-1-9)
所以,需要對邏輯回歸和隨機梯度下降公式做一些調整。首先,假設數據不是分布式存儲的,而是都存放在一處的。基于樣本![]() 和對應的標簽
和對應的標簽![]() ,可以學習到邏輯回歸模型
,可以學習到邏輯回歸模型![]() 。基于n個
。基于n個![]() 組成的訓練集
組成的訓練集![]() ,平均損失函數為
,平均損失函數為
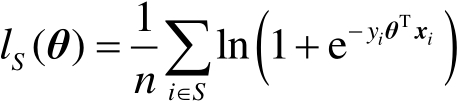
(3-1-10)
反之,基于訓練樣本的樣本數量為![]() 的子集
的子集![]() 計算的隨機梯度為
計算的隨機梯度為
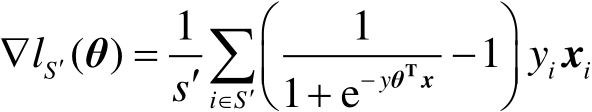
(3-1-11)
雖然模型學習只需要梯度,而不需要損失,但是這里采用簡單交叉驗證,在大小為![]() 的驗證集
的驗證集![]() 上監測損失函數
上監測損失函數![]() 以便提前終止訓練,防止模型過擬合。
以便提前終止訓練,防止模型過擬合。
在加法同態加密算法下,我們需要考慮如何計算邏輯回歸中的損失和梯度的近似值。為了實現這一點,我們在![]() 的周圍進行
的周圍進行![]() 的泰勒級數展開,即
的泰勒級數展開,即
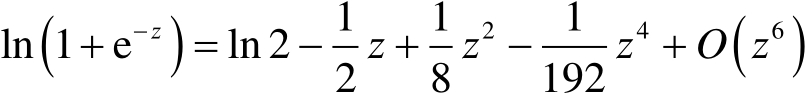
(3-1-12)
在驗證集![]() 上評估的損失函數
上評估的損失函數![]() 的二階近似為
的二階近似為
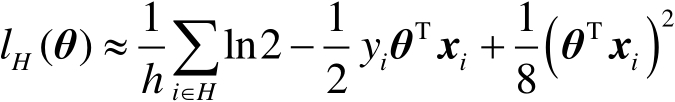
(3-1-13)
上式中對于任意的![]() ,有
,有![]() 。為了區分,數據集
。為了區分,數據集![]() 上的梯度為
上的梯度為
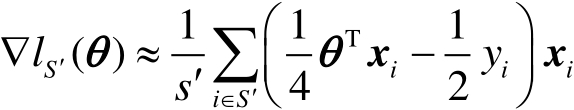
(3-1-14)
接下來,為損失和梯度添加加密的掩碼![]() ,則數據集
,則數據集![]() 上的加密梯度為
上的加密梯度為
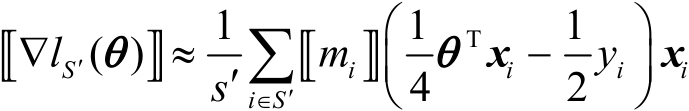
(3-1-15)
驗證集![]() 上的加密損失為
上的加密損失為
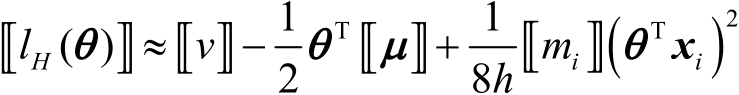
(3-1-16)
式中,![]() ,
,![]() 。常數項
。常數項![]() 與最小化無關,之后將其設置為0。
與最小化無關,之后將其設置為0。
下面介紹如何用隨機梯度下降訓練縱向聯邦邏輯回歸模型。假設第一階段的實體對齊已經完成,也就是參與方A和B具有相同的![]() 行數據。用矩陣
行數據。用矩陣![]() 表示完整的數據集,這個矩陣的數據是由參與方A和B的數據并列而成的,而不是真實地存儲于同一處,即
表示完整的數據集,這個矩陣的數據是由參與方A和B的數據并列而成的,而不是真實地存儲于同一處,即
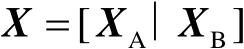
(3-1-17)
只有參與方A具有標簽![]() ,
,![]() 可以分解為
可以分解為
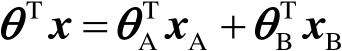
(3-1-18)
算法1是安全邏輯回歸的計算流程,由第三方C執行。首先,C方創建一組密鑰對,將公鑰分享給A方和B方。然后,C方將加密的掩碼![]() 發送給A方和B方,這里的訓練過程允許在C方忽略劃分驗證集和小批量采樣的情況下完成。算法2對損失進行了初始化,并緩存了
發送給A方和B方,這里的訓練過程允許在C方忽略劃分驗證集和小批量采樣的情況下完成。算法2對損失進行了初始化,并緩存了![]() 用于計算之后的邏輯損失。此外,任何隨機梯度算法都可以用于優化,如果選擇隨機平均梯度[46](Stochastic Average Gradient,SAG)進行實驗,那么C方會保留之前的梯度。算法3用于監視驗證集上
用于計算之后的邏輯損失。此外,任何隨機梯度算法都可以用于優化,如果選擇隨機平均梯度[46](Stochastic Average Gradient,SAG)進行實驗,那么C方會保留之前的梯度。算法3用于監視驗證集上![]() 的損失以便提前停止訓練。在任何加法同態加密方案下,損失的計算成本都很高。算法4是梯度的安全計算過程,在算法1的每輪計算中都需調用它。可以看到,在整個過程中,唯一清楚發送的、A方和B方可以共享的信息只有模型
的損失以便提前停止訓練。在任何加法同態加密方案下,損失的計算成本都很高。算法4是梯度的安全計算過程,在算法1的每輪計算中都需調用它。可以看到,在整個過程中,唯一清楚發送的、A方和B方可以共享的信息只有模型![]() 和每批數據
和每批數據![]() 。其他所有信息都是加密的,C方只接收到
。其他所有信息都是加密的,C方只接收到![]() 。更詳細的過程可參考文獻[46]。
。更詳細的過程可參考文獻[46]。






縱向聯邦線性回歸:線性回歸是統計學習中最基礎的方法。
一般來說,基于梯度下降的方法來訓練線性回歸模型。現在需要對模型訓練中涉及的損失和梯度進行安全計算。其中,學習率為![]() ,
,![]() 為正則化參數,
為正則化參數,![]() 為數據集,模型參數
為數據集,模型參數![]() 分別對應了特征
分別對應了特征![]() 和
和![]() ,則模型的訓練目標表示為
,則模型的訓練目標表示為
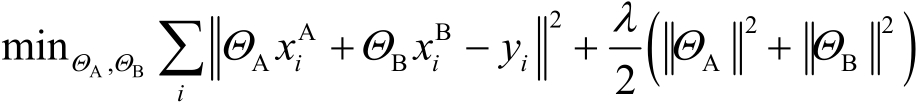
(3-1-19)
讓![]() ,
,![]() ,則加密的損失為
,則加密的損失為
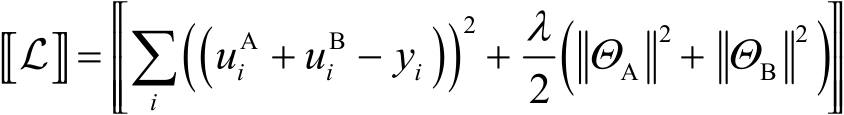
(3-1-20)
式中,同態加密算法定義為![]() 。讓
。讓![]() ,
,![]() ,
,![]() ,則有
,則有
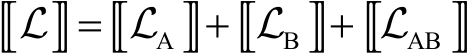
(3-1-21)
同理,讓![]() ,則梯度表示為
,則梯度表示為
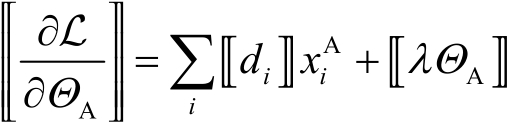
(3-1-22)
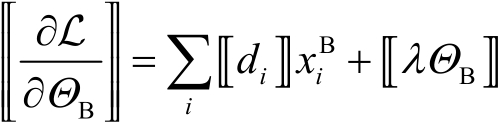
(3-1-23)
模型的具體訓練過程如下。
(1)A方和B方對參數![]() 、
、![]() 做初始化,C方生成密鑰對,將公鑰發送給A方和B方。
做初始化,C方生成密鑰對,將公鑰發送給A方和B方。
(2)A方計算![]() 、
、![]() 并將其發送給B方;B方計算
并將其發送給B方;B方計算![]() 、
、![]() 、
、![]() ,然后發送
,然后發送![]() 給A方,發送
給A方,發送![]() 給C方。
給C方。
(3)A方初始化一個隨機數![]() ,計算
,計算 并將其發送給C方;B方初始化一個隨機數
并將其發送給C方;B方初始化一個隨機數![]() ,計算
,計算 并將其發送給C方;C方根據解密后的損失
并將其發送給C方;C方根據解密后的損失![]() 判斷模型是否收斂,并對加密梯度解密后再發送
判斷模型是否收斂,并對加密梯度解密后再發送![]() 和
和![]() 給對應的A方和B方。
給對應的A方和B方。
(4)A方和B方減去之前引入的隨機數,依據得到的真實梯度對參數![]() 、
、![]() 進行更新。
進行更新。
模型的評估過程如下:
(1)C方分別向A方和B方發送樣本ID ![]() 。
。
(2)A方計算![]() 并將其發送給C方,B方計算
并將其發送給C方,B方計算![]() 并將其發送給C方;C方獲得結果
并將其發送給C方;C方獲得結果![]() 。
。
基于上述訓練過程,可以看到訓練中的信息傳輸并沒有暴露數據隱私,A方和B方的數據一直保存在本地,即便泄露給C方數據也未必會被視為侵犯隱私。不過為了盡可能地預防數據被泄露給C方,A方和B方可以考慮加入加密隨機掩碼進一步保護數據。從而,A方和B方完成了在聯邦環境下協同訓練一個共有模型。由于在構建模型時,每個參與方得到的損失和梯度應該與不限制隱私、將數據聚集在一處訓練模型時學習的損失和梯度一致,所以該聯邦模型理應是沒有損失的,即模型訓練的成本會受到數據加密所造成的通信和計算資源的影響。由于在每輪訓練中,A方和B方互相傳送的數據會隨重合樣本量的變化而變化,因此該算法的效率能通過采取分布式計算技術得到提高。
從安全性方面來看,在訓練過程中并沒有向C方泄露任何數據,C方得到的都是加密的梯度和隨機數,與此同時,加密矩陣的安全性也是有保證的。在上述訓練過程中,雖然A方在每步都學習自身的梯度,但A方并不能依照公式![]() 就從B方處獲得相關信息,因為要求解n個未知數就必須有至少n個方程才能確定方程的唯一解,這一必要性保證了標量積計算的安全性。在此處,我們假定樣本數
就從B方處獲得相關信息,因為要求解n個未知數就必須有至少n個方程才能確定方程的唯一解,這一必要性保證了標量積計算的安全性。在此處,我們假定樣本數![]() 遠大于特征數
遠大于特征數![]() 。同理,B方也無法從A方處獲得任何相關的信息,從而證明了該過程的隱私性。值得注意的是,假設兩個參與方都是半誠實的,但是當存在一個參與方是惡意攻擊者時,它會偽造輸入進行欺騙,如A方僅提交一個只有一個不為零的特征的非零輸入,則系統可以識別出該輸入的這一特征
。同理,B方也無法從A方處獲得任何相關的信息,從而證明了該過程的隱私性。值得注意的是,假設兩個參與方都是半誠實的,但是當存在一個參與方是惡意攻擊者時,它會偽造輸入進行欺騙,如A方僅提交一個只有一個不為零的特征的非零輸入,則系統可以識別出該輸入的這一特征![]() ,但系統無法識別出
,但系統無法識別出![]() 或
或![]() ,同時偏差會使得之后的訓練結果失真,從而告知另一參與方停止訓練。在結束時,A方或B方都不會知曉對方的數據結構,都只能得到和自己的特征有關的參數,達不到聯合訓練的效果。在推斷時,雙方需要使用上述評估步驟來共同預測結果,這同樣也不會暴露數據,更詳細的過程可參考文獻[2]。
,同時偏差會使得之后的訓練結果失真,從而告知另一參與方停止訓練。在結束時,A方或B方都不會知曉對方的數據結構,都只能得到和自己的特征有關的參數,達不到聯合訓練的效果。在推斷時,雙方需要使用上述評估步驟來共同預測結果,這同樣也不會暴露數據,更詳細的過程可參考文獻[2]。
縱向聯邦泊松回歸:泊松回歸是針對事件發生次數利用特征構建的回歸模型,滿足事件之間的發生是相互獨立的,事件的發生次數服從泊松分布。在模型訓練之前,需要對不同參與方的數據進行基于隱私保護下的實體對齊,然后基于重疊樣本構建聯邦模型,訓練過程如圖3-1-2所示。
(1)A方和B方各自對參數![]() 、
、![]() 做初始化,C方生成密鑰對并發送公鑰給A方和B方,A方將用公鑰加密后的
做初始化,C方生成密鑰對并發送公鑰給A方和B方,A方將用公鑰加密后的![]() 傳輸給B方。
傳輸給B方。
(2)B方在拿到加密數據后,結合目標值![]() ,計算可得
,計算可得![]() ,然后用公鑰加密后將
,然后用公鑰加密后將![]() 傳輸給A方。
傳輸給A方。
(3)B方結合本地數據計算得到B方梯度![]() ,A方結合本地數據計算得到A方梯度
,A方結合本地數據計算得到A方梯度![]() ,然后B方和A方分別將各自的梯度
,然后B方和A方分別將各自的梯度![]() 和
和![]() 發送給C方。
發送給C方。
(4)C方將獲得的梯度![]() 、
、![]() 進行匯總和解密后得到一個完整的梯度,最后將優化后的完整梯度拆分成新的
進行匯總和解密后得到一個完整的梯度,最后將優化后的完整梯度拆分成新的![]() 和
和![]() ,并將其分發給對應的B方和A方。
,并將其分發給對應的B方和A方。
(5)B方和A方利用優化后的梯度對模型進行更新,同時C方根據B方設置的停止標準,在每次迭代結束時判斷聯邦模型是否收斂。如果收斂,那么C方分別向B方和A方發送停止迭代標識。
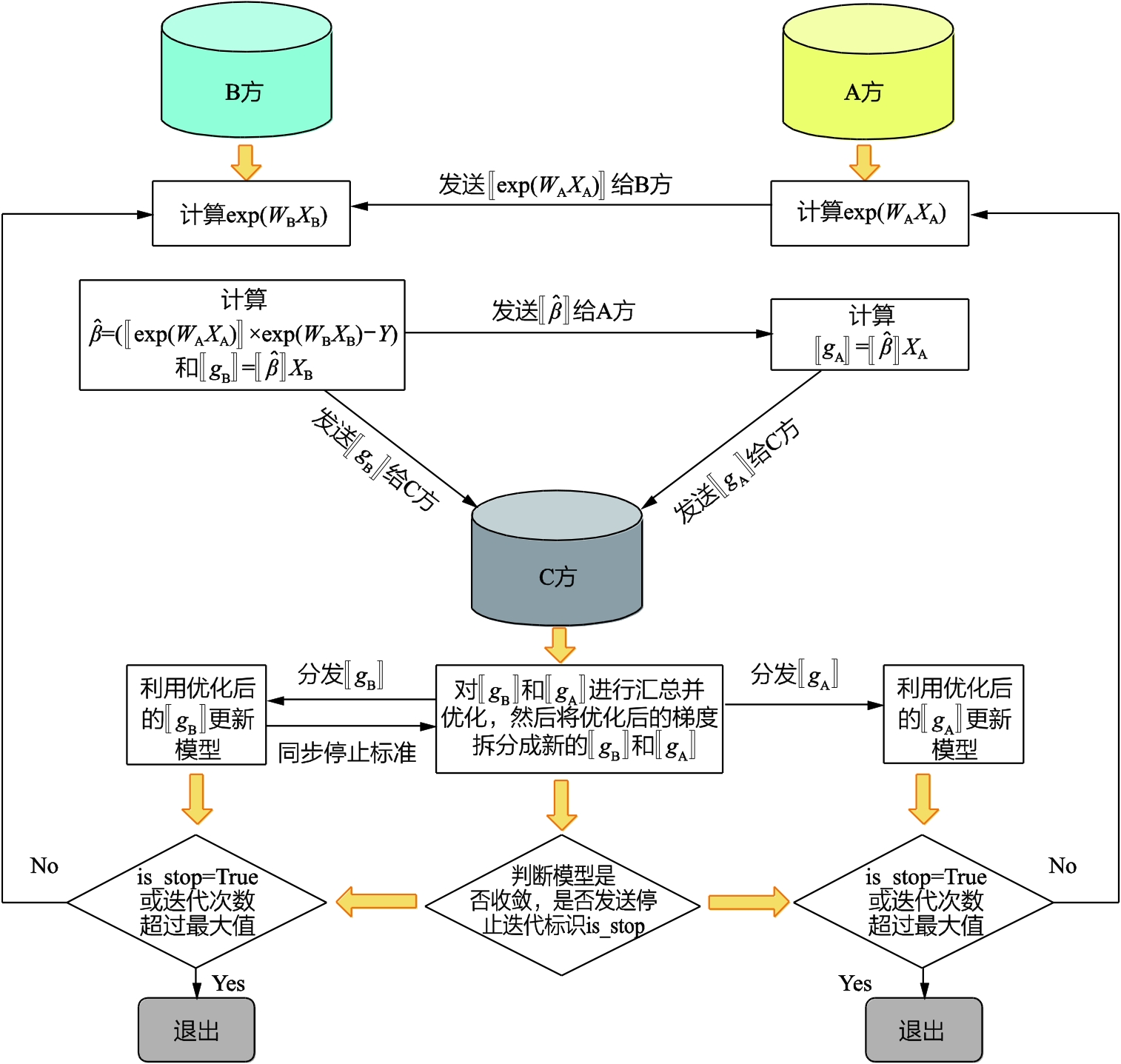
圖3-1-2 縱向聯邦泊松回歸模型的訓練過程