緒論 數(shù)學(xué)源于生活

歷史上的數(shù)學(xué)故事

一個國家只有數(shù)學(xué)蓬勃發(fā)展，才能展現(xiàn)出它國力的強(qiáng)大。

——拿破侖

提起數(shù)學(xué)，很多人都承認(rèn)它的重要性，但同時又有一種畏懼心理，認(rèn)為數(shù)學(xué)是抽象的、難學(xué)的。那么，數(shù)學(xué)是不是真的高高在上、拒人于千里之外呢？其實不然。俄羅斯數(shù)學(xué)家羅巴切夫斯基曾說：“不管數(shù)學(xué)的任一分支是多么抽象，總有一天會應(yīng)用到這實際世界上。”我國數(shù)學(xué)家華羅庚也曾說：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之變，生物之謎，日用之繁，無處不用數(shù)學(xué)。”這些話精彩地描述了數(shù)學(xué)與生活的密切聯(lián)系。

實際上，數(shù)學(xué)很親民。數(shù)學(xué)源于生活，高于生活，又回歸生活。生活中處處都有數(shù)學(xué)的蹤影。既然這樣，那為什么許多人仍會覺得數(shù)學(xué)高高在上呢？歸根結(jié)底，還是因為我們的數(shù)學(xué)教育與生活聯(lián)系得不夠密切。雖然我國新制定的《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)》十分強(qiáng)調(diào)數(shù)學(xué)與現(xiàn)實生活的聯(lián)系，指出“數(shù)學(xué)是人們生活、勞動和學(xué)習(xí)必不可少的工具，能夠幫助人們處理數(shù)據(jù)，進(jìn)行計算、推理和證明”，但是，在應(yīng)試的壓力下，目前的數(shù)學(xué)教育還是以刷海量的、與生活缺乏聯(lián)系且枯燥的題目為主。

好奇心是一切學(xué)習(xí)活動的內(nèi)驅(qū)力和催化劑。如果我們在生活中注意觀察，少一點兒想當(dāng)然，多一點兒好奇，并在此基礎(chǔ)上對孩子加以適當(dāng)引導(dǎo)，讓孩子在日常生活中感受數(shù)學(xué)的奧妙與數(shù)學(xué)之美，對提升孩子的數(shù)學(xué)學(xué)習(xí)興趣和啟發(fā)孩子的數(shù)學(xué)思維能起到非常積極的作用。

事實上，歷史上數(shù)學(xué)的發(fā)展也與人們的生活密不可分。幾何學(xué)的誕生就是一個很好的例子。相傳4000年前，埃及的尼羅河每年洪水泛濫，總是淹沒兩岸的土地，水退后，土地的界線變得不分明。當(dāng)時，埃及的勞動人民為了重新測出被洪水淹沒的土地的地界，每年都要進(jìn)行土地測量，因此積累了許多測量土地方面的知識，從而產(chǎn)生了幾何學(xué)的雛形。

下面我要介紹的三則歷史上的數(shù)學(xué)故事都與生活緊密相關(guān)。第一個是許多人都熟知的七橋問題，第二個是拿破侖巧用幾何學(xué)打勝仗的逸事，最后一個則是曾經(jīng)的世界著名數(shù)學(xué)難題之一 ——“四色問題”。

七橋問題與圖論的誕生

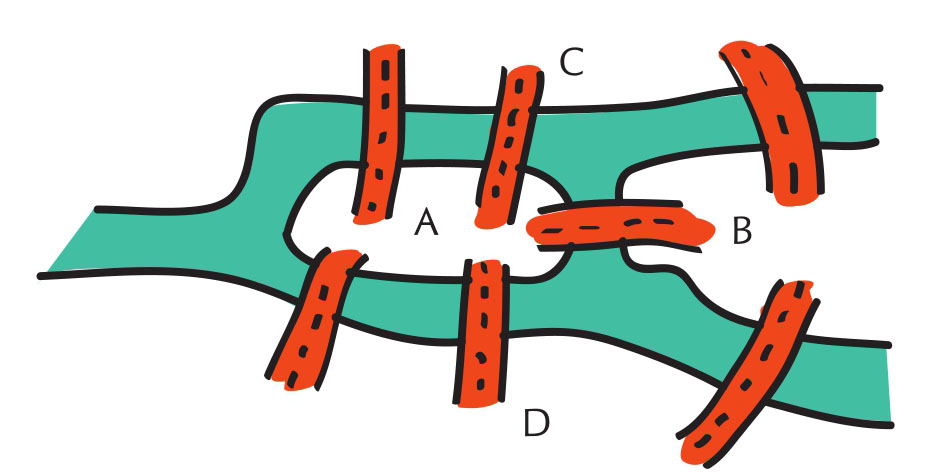
圖論誕生的故事為人們所津津樂道，其原因之一就在于它來源于生活。相傳，哥尼斯堡有一條河，河上有兩個小島，島上有7座橋，其中，有6座橋連接著島與河岸，最后一座橋則連接著兩個島。島上有古老的哥尼斯堡大學(xué)和教堂，還有哲學(xué)家康德的墓地和塑像。城中的居民（尤其是大學(xué)生們）經(jīng)常沿河過橋散步。有一天，一個好奇的人提出如下問題：

一個散步者能否一次走遍7座橋，而且每座橋只許通過一次，最后仍回到起始地點？

這就是著名的七橋問題。它看似簡單，然而很多人做了不懈的嘗試卻始終未能找到答案。因此，一群大學(xué)生就寫信給當(dāng)時在圣彼得堡科學(xué)院任職的二十多歲的天才數(shù)學(xué)家歐拉，請他分析一下這個問題。孰料，這一請教影響深遠(yuǎn)，開創(chuàng)了圖論這一數(shù)學(xué)分支。

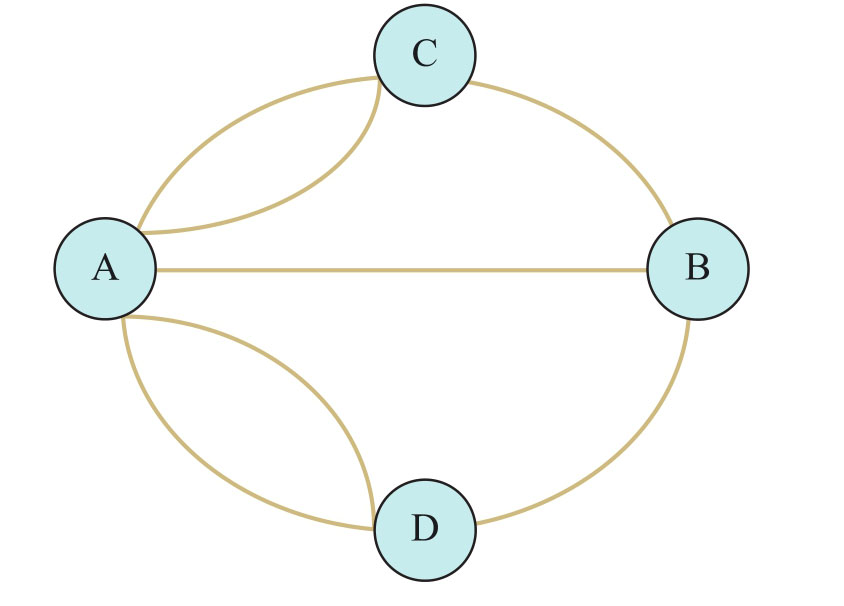
歐拉用簡單的幾何圖形來表示陸地和橋，如下圖所示，于是七橋問題就轉(zhuǎn)變?yōu)槟芊褚淮吻覂H一次遍歷圖中所有的邊。經(jīng)過一番研究后，他得出了一個圖形能達(dá)到該要求（或稱圖形能一筆畫）的充要條件：

①圖形必須是連通的；

②圖中的“奇點”（也就是一個頂點連接的邊數(shù)為奇數(shù)）個數(shù)是0或2。

如果圖中的奇點個數(shù)為0，則該圖可以一筆畫，并且可以回到起點，對應(yīng)的路徑也稱為歐拉回路。而如果圖中的奇點個數(shù)是2，則圖是可以一筆畫的，但無法回到起點，所對應(yīng)的歐拉路徑一定是以圖中的一個奇點為起點，而以另一個奇點為終點。

七橋問題為何無解？原因在于它存在4個奇點。直觀地想一下，要經(jīng)過圖中所有邊而不重復(fù)，那么所有既非起點又非終點的節(jié)點所連的邊數(shù)必定為偶數(shù)（一進(jìn)一出必須相匹配），因此4個奇點的圖形是不能一筆畫的。

其實，我們在寫漢字的時候也會碰到一筆畫問題。有興趣的讀者可以嘗試一下，如日、中、串、木、蟲等漢字能否一筆畫？英文中也有類似問題，如26個大寫的英文字母能否一筆畫？

歐拉是數(shù)學(xué)史上公認(rèn)的最偉大的4位數(shù)學(xué)家之一，其余3人分別是阿基米德、牛頓和高斯。歐拉不僅在數(shù)學(xué)上做出了偉大的貢獻(xiàn)，而且把數(shù)學(xué)用到了整個物理領(lǐng)域。他是科學(xué)史上最多產(chǎn)的數(shù)學(xué)家。據(jù)統(tǒng)計，他一生的專著和論文有800多種。他在數(shù)學(xué)上的貢獻(xiàn)覆蓋了從數(shù)論、函數(shù)、微積分到圖論等多個領(lǐng)域。正因為他的貢獻(xiàn)太多，以至于談到歐拉公式時，我們都不禁要追問一句：慢著，你說的是哪個歐拉公式？

酷愛數(shù)學(xué)的拿破侖

數(shù)學(xué)與人們的日常生活密不可分，甚至能左右一場戰(zhàn)斗的勝負(fù)。拿破侖是法蘭西第一帝國的締造者。提起拿破侖，很多人都會對這位軍事家的杰出才能嘖嘖稱贊，也有人為他的滑鐵盧之?dāng)∩罡型锵В€有人對他與約瑟芬的曠世愛情唏噓不已……但鮮為人知的是，拿破侖是一位極具天賦的數(shù)學(xué)愛好者，他為法國數(shù)學(xué)事業(yè)的發(fā)展做出了巨大貢獻(xiàn)，他的數(shù)學(xué)天賦為他取得戰(zhàn)場的勝利立下了汗馬功勞。

拿破侖是炮兵學(xué)院出身，在校期間，他潛心研究過彈道學(xué)。拿破侖的專業(yè)技術(shù)非常厲害，在土倫戰(zhàn)役中，他指揮炮兵部隊一打一個準(zhǔn)，十分驚人，他也從此脫穎而出。后來他在軍隊中積極推廣先進(jìn)的數(shù)學(xué)方法，如三角函數(shù)、微分方程等。拿破侖對炮兵和海軍軍官工程師提出了很高的要求，以至于他的大炮打到哪里，工程師的圖就得畫到哪里。拿破侖在幾何學(xué)上頗有造詣，甚至有專門以拿破侖命名的“拿破侖定理”和“拿破侖問題”。

拿破侖的數(shù)學(xué)才華對他在戰(zhàn)場上屢創(chuàng)奇跡起到了至關(guān)重要的作用。據(jù)傳，1805年，拿破侖率軍與普魯士、俄國聯(lián)軍在萊茵河南北兩岸對陣。兩軍都想向?qū)Ψ疥嚨亻_炮，但是不知寬度的萊茵河成為雙方的阻礙，沒有精確射程的炮擊成了浪費彈藥的競賽。在這種情況下，誰能率先測量出河的寬度，誰就能占得先機(jī)。

為了解決這個難題，拿破侖每天遠(yuǎn)眺萊茵河，在岸邊來回踱步。有一次，他偶然發(fā)現(xiàn)，對岸的邊線（北岸線）恰巧擦著自己戴的軍帽檐，于是，計上心來。他在這個地點做了一個記號，然后沿著萊茵河的垂直方向一步一步往后退，一直退到萊茵河南岸線也擦著自己軍帽檐的地方，停下來又做了個記號。拿破侖讓部下丈量出這兩個記號之間的距離，并告訴部下：“這就是萊茵河的寬度。”

當(dāng)天傍晚，法軍大炮向?qū)Π稊耻婈嚨厣鋼簟Ｅ趶椌拖耖L了眼睛般，紛紛飛入敵營。敵軍頓時大亂，全線潰敗，而法軍憑借拿破侖的數(shù)學(xué)才華大獲全勝。

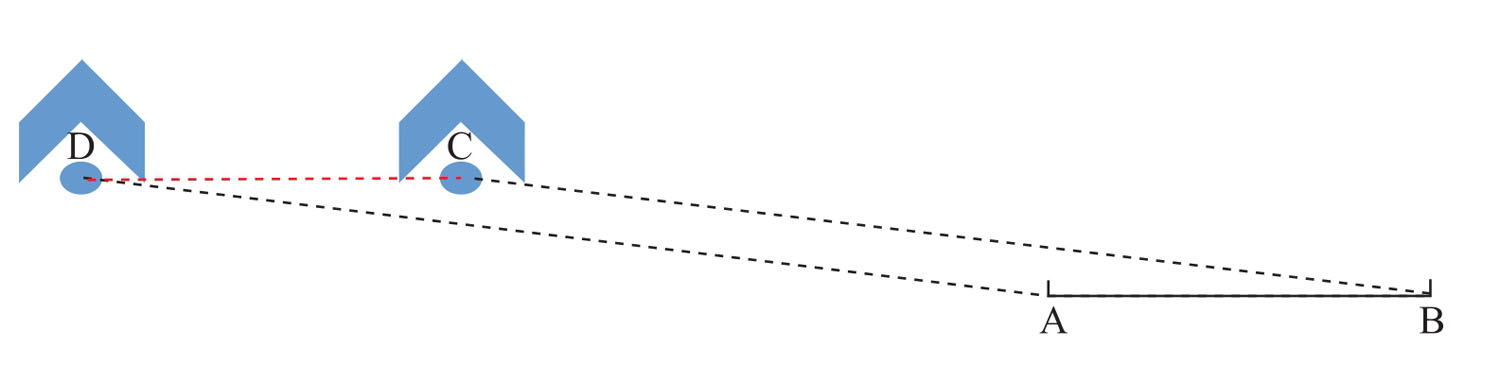
這則逸事是理論聯(lián)系實際在戰(zhàn)場上的最佳體現(xiàn)。為什么拿破侖所說的那兩個點之間的距離就是萊茵河的寬度呢？利用小學(xué)的平面幾何知識就能證明這一點。如下圖所示，A、B分別是萊茵河的南岸和北岸。第一次，拿破侖的眼睛C、軍帽檐與北岸B呈三點一線，即圖中所示的BC；第二次，拿破侖后退到D的位置，眼睛、軍帽檐與法軍這一側(cè)的南岸A呈三點一線，即圖中的AD。由于兩次的直線平行，ABCD構(gòu)成了平行四邊形，因此，萊茵河AB的寬度與CD的長度相等。

拿破侖非常重視法國的數(shù)學(xué)教育，他曾說：“一個國家只有數(shù)學(xué)蓬勃發(fā)展，才能展現(xiàn)出它國力的強(qiáng)大。”他認(rèn)為，人才培養(yǎng)的關(guān)鍵是教育。從1802年至1808年，他頒布了一系列法令，確立了法國精英制大學(xué)校的高等教育模式，旨在培養(yǎng)理論聯(lián)系實際、既有知識又有應(yīng)用技術(shù)的人才。實際上，目前法國最好的兩所精英大學(xué)——巴黎高等師范學(xué)院（école normale supérieure de Paris）和巴黎綜合理工學(xué)院（école Polytechnique），就是在拿破侖時代組建的。拿破侖極為珍惜人才。1814年，當(dāng)反法聯(lián)軍兵臨城下，法國兵員短缺，有人提議調(diào)巴黎理工學(xué)院的學(xué)生參加戰(zhàn)斗，但是拿破侖說：“我不愿為取金蛋而殺掉我的老母雞。”這句名言后來被鐫刻在巴黎綜合理工學(xué)院梯形大教室的天花板上。

地圖著色與四色定理

生活不僅為數(shù)學(xué)提供了用武之地，而且為數(shù)學(xué)提供了廣泛的素材。可以說，離開了生活，數(shù)學(xué)就成為無源之水。

兒子的昍床頭掛著一幅中國地圖，該地圖用了5種顏色來對每個省份著色，確保任何兩個相鄰的省份擁有不同的顏色。

相信每個人都看過地圖，只不過大部分人對地圖的顏色并不關(guān)心。但是，真的需要用5種顏色來著色嗎？

一個半世紀(jì)以前，畢業(yè)于倫敦大學(xué)的弗南西斯·格思里在一家科研機(jī)構(gòu)做地圖著色時，發(fā)現(xiàn)了一種有趣的現(xiàn)象：每幅地圖最多使用4種顏色著色，就可以使得有共同邊界的國家都被著上不同的顏色。[1]

弗南西斯·格思里沒有想到的是，他的這一發(fā)現(xiàn)連當(dāng)時的數(shù)學(xué)家哈密爾頓爵士都未能證明，最終“四色猜想”成為與費馬大定理和哥德巴赫猜想并列的世界近代三大數(shù)學(xué)難題之一。可見，只要我們善于觀察、思考和發(fā)現(xiàn)，世界數(shù)學(xué)難題就在我們身邊。也許你就是下一個世界數(shù)學(xué)難題的提出者。

一個多世紀(jì)以來，數(shù)學(xué)家們?yōu)榱俗C明這條定理絞盡腦汁，所引進(jìn)的概念與方法刺激了拓?fù)鋵W(xué)與圖論的發(fā)展。四色問題的證明也出現(xiàn)多次烏龍，好幾次證明方案最后都被證明是錯的，不過這些錯誤都為后續(xù)證明提供了寶貴的經(jīng)驗。

20世紀(jì)70年代，計算機(jī)功能的提升使窮舉法如虎添翼。直到1976年，人們才利用計算機(jī)強(qiáng)大的計算能力，用了1200多個小時，作了100億個判斷，最終證明了四色定理。

有人專門為四色問題的歷史寫了本書，叫《四色足夠》（Four Colors Suffice）。但是，簡單的四色問題采用這種暴力窮舉的證明方法，完全喪失了數(shù)學(xué)本該有的簡潔與美。如今，四色定理依然期待著一個與其問題描述本身相匹配的優(yōu)雅證明。

---

[1] 這個結(jié)論有個前提條件，就是這些國家或地區(qū)不能像曾經(jīng)的“日不落帝國”英國一樣有海外飛地，也就是說一個國家的版圖必須連在一起。