1.2　優化驅動的設計方法研究現狀

本節將圍繞拓撲優化設計、多學科設計優化和可靠性設計優化3類優化驅動的設計方法進行國內外研究現狀綜述。

1.2.1　拓撲優化設計研究現狀

拓撲優化主要運用于產品的概念設計階段，它完全不依賴于初始參考構型和工程經驗，能夠根據不同的設計需求（目標函數），在規定的設計區域內創新性地構造出結構的最佳構型。早期的拓撲優化設計主要運用于以桁架為代表的離散體結構[10-13]。連續體結構拓撲優化思想則是由Bends?e和Kikuchi[14]在1988年的研究論文中首次提出，經過三十多年的發展，學者們提出了多種行之有效的拓撲優化設計方法，包括：均勻化方法[14]、帶懲罰函數的固體各向同性微結構（solid isotropic microstructures with penalization，SIMP）方法[15-18]、水平集方法（level set method）[19-22]、進化結構優化（evolutionary structural optimization，ESO）方法[23]、可移動變形組件（moving morphable components，MMC）方法[24]，[25]以及獨立-連續-映射（independent continuous mapping，ICM）方法[26]，[27]等。雖歷經幾十年的發展，學者們提出了各具特色的拓撲優化設計方法，但由于描述模型的不足、算法和問題的復雜性導致拓撲優化在解決工程設計問題時尚存在缺陷。在各類拓撲優化設計技術中，學者們通常采用基于有限元的方法對結構應變場進行分析，這將導致結構邊界形狀依賴于有限元網格，即產生模糊或鋸齒狀的結構邊界。因此，一些基于單元密度的拓撲優化方法無法獲得完整的結構邊界幾何信息，導致其優化結果無法直接導入CAE/CAD軟件進行分析和再設計。基于水平集的拓撲優化設計方法能夠獲得清晰、光滑的結構邊界。其基本原理是將結構的動態邊界隱式地嵌入到高一維的水平集函數中，通過選擇合適的速度場以驅動結構邊界逐步優化。該幾何描述方式確保了最優拓撲的清晰結構邊界和完整幾何信息，能夠直接與CAE/CAD軟件集成。由于基于水平集的拓撲優化設計方法集成了形狀導數的概念，故其能夠同時開展結構的形狀和拓撲優化。然而，傳統的水平集方法在解決拓撲優化設計問題中還存在許多不足，如：數值計算復雜，迭代步數多；優化結果依賴于初始孔洞的數量和位置；基于梯度的高效優化算法（如優化準則法、移動漸近線法）無法直接應用；缺乏針對動力學、微尺度、多尺度等優化問題的應用研究等。上述問題還有待進一步探討和研究。因此，本節接下來將重點對水平集方法進行綜述。

1．水平集方法研究現狀

與基于單元密度的拓撲優化方法不同，水平集方法是一類基于邊界描述的方法。水平集方法能夠通過直接驅動結構邊界來達到優化結構拓撲和形狀的目的，因此可以保證所獲得優化結構具有清晰、光滑的邊界。最經典的水平集方法并不是一開始就應用于結構拓撲優化設計研究，其最早是應用于追蹤曲面／曲線的演化過程[19]。該方法的主要思想是將低一維的運動邊界作為零水平面，并將該零等值面嵌入到高一維的水平集函數中，通過設置合適的邊界速度場，即可驅動水平集函數運動，從而間接地帶動零水平面（運動界面）演化。該方法在圖形圖像處理、火焰燃燒、晶體生長、多相流、計算機視覺等運動界面追蹤領域得到了廣泛的應用[28]。利用水平集方法描述運動邊界具有諸多優點，如：方便靈活地反映曲線／曲面的形狀和拓撲特征；容易獲得運動邊界的幾何特征（如法矢和曲率等）；能夠在離散的網格上利用有限差分法對水平集方程進行數值求解，并利用空間導數計算水平集函數Φ的梯度；Hamilton-Jacobi偏微分方程的黏性解理論保證其能夠找到Lipschitz連續的唯一解[29]。

考慮到水平集方法在處理運動邊界方面的獨特優勢，Sethian和Wiegmann[20]在2000年首次將該方法引入結構拓撲優化設計領域，實現了結構形狀和拓撲優化聯合優化，實現了典型結構件的滿應力設計。在該研究中，結構的邊界被隱式地嵌入到高一維的水平集函數中，基于形狀靈敏度分析建立了結構邊界演化的速度場，最終構建了Hamilton-Jacobi偏微分方程，通過對偏微分方程進行迭代求解，實現了結構的優化設計。隨后，Osher和Santosa[30]在水平集方法框架中引入了目標泛函的形狀梯度，從而建立了形狀梯度與速度場間的聯系。這一工作被Allaire等[22]和Wang等[21]進一步拓展和改進，從而形成了水平集與形狀導數相結合的新框架，至今仍然是最流行的方法之一。基于以上工作，學者們對基于水平集方法的拓撲優化設計開展了深入而廣泛的研究。莊春剛等[31]為解決標準水平集方法無法生成新孔洞的缺陷，利用vonMises應力準則來構造新孔。Xia等[32]提出了一種半拉格朗日策略來求解Hamilton-Jacobi偏微分方程，增加了迭代步長，減少了優化所需的迭代步數。榮見華[33]對水平集方法進行改進，解決了傳統水平集方法導致結構邊界進化停滯的問題。Luo等[29]提出了一種新的半隱式格式水平集方法，利用半隱式加性分裂算子求解Hamilton-Jacobi偏微分方程。

盡管水平集方法在處理運動邊界時具有天然優勢，然而利用傳統水平集方法解決結構拓撲優化問題時尚存在以下缺陷：①高一維的水平集函數在優化過程中可能會變得過于平坦或過于陡峭。這是由于零水平面所對應的水平集函數不唯一所造成的。過平或過陡的水平集面會導致數值計算的穩定性問題，因此在應用傳統水平集方法時需要不斷將水平集函數重新初始化為一種符號距離函數。而該重新初始化操作通常獨立于優化過程之外，額外地增加了優化成本。②為滿足穩定性和收斂性要求，在求解Hamilton-Jacobi偏微分方程時需要滿足Courant-Friedrichs-Lewy(CFL)條件，即時間步長需要小于單個水平集網格的間隔長度。換句話講，水平集網格尺度需要足夠小，才能滿足計算精度要求，這也將導致優化迭代時間的顯著增加。③為了驅動水平集函數的演化，需要將邊界上的速度場擴展到整個結構設計域或邊界上的窄帶區域。然而通過形狀導數得到的速度場主要定義在結構邊界上，因此需要求解一套額外的Hamilton-Jacobi偏微分方程才能實現速度場的擴展。以上問題一定程度上限制了傳統水平集方法的應用。

2．參數化水平集方法研究現狀

為了克服傳統水平集方法的缺陷，學者們開展了對水平集方法的改進研究。Yamada等[34]在水平集方法中嵌入了一種虛擬界面能量形式，解決了連續體剛度拓撲優化設計和柔性機構拓撲優化設計問題。vanDijk等[35]提出了一種顯式的水平集拓撲優化設計方法。Dunning和Kim[36]運用序列線性規劃方法求解基于水平集的拓撲優化設計模型，提升了方法的求解效率。Guo等[37]利用水平集方法實現了結構拓撲優化設計中的顯式特征控制。

除上述方法之外，參數化水平集方法被認為是水平集方法中最有效的改進形式之一[38]。2006年Wang和Wang[39]采用一種全局支撐的徑向基函數（globally supported radialbasis function，GSRBF）對離散點上的水平集函數進行插值，從而通過改變徑向基函數（radialbasis function，RBF）插值的擴展系數來實現水平集函數及結構邊界的更新，最終實現了結構剛度最大化的拓撲優化設計。在該方法中，擴展系數的迭代更新采用了最速下降法，該算法的效率和通用性尚有待進一步的改進。為了降低由于GSRBF稠密插值矩陣所導致的高昂計算成本，Ho等[40]利用動態徑向基函數插值節點和單位分解法，提出了改進的參數化水平集方法。此外，Luo等[41]引入緊支撐徑向基函數（compactly supported radial basis function，CSRBF）插值技術，提出了基于CSRBF的參數化水平集方法，并將其運用于結構剛度優化[42]、柔性機構優化[43]、材料微結構優化[44]，[45]等不同應用場景。

對于基于RBF插值的參數化水平集方法而言，插值精度和效率對方法的性能有重要影響。基于CSRBF的插值機制在參數化水平集中應用十分廣泛[41-45]，其主要原因在于CSRBF的插值矩陣較為稀疏，能夠很大程度上降低水平集函數插值的計算成本。理論上，CSRBF的支撐僅定義在當前樣本點附近的有限區域內，對該樣本點的水平集函數進行插值時并沒有考慮設計域內所有插值節點的影響，因此CSRBF的插值效率高，而精度較低[46]。對于材料使用量較多或對結構邊界敏感度較低的結構拓撲優化設計問題，采用CSRBF插值具有不錯的效果。相較于CSRBF，GSRBF有較高的插值精度[46]，通常可以找到更優的結構設計方案，但其插值和優化的效率十分低下，導致對于大規模拓撲優化問題應用困難。由此可見，對于參數化水平集方法而言，在平衡其優化效率和優化效果方面具有較大的改進空間。

自拓撲優化研究興起以來，各類優化方法不斷涌現，較為經典的方法有均勻化方法、變密度法、進化結構優化法、水平集法、移動可變形組件法和獨立-連續-映射法等。從拓撲優化方法的發展來看，各類方法均具有獨特的優勢，同時又存在一定的應用缺陷。通常而言，可從建模特點、求解效率和操作難易程度來不斷改進和完善拓撲優化方法。在拓撲優化的應用方面，隨著增材制造技術的推廣和成熟，復雜的結構形式能夠被該類制造工藝加工成型，使得拓撲優化受到工程界的廣泛重視，并成為產品設計中不可或缺的設計工具。拓撲優化設計技術是基于“優化”的思想，通過科學的手段，智能地獲得創新性結構設計方案，且該方案往往是無法通過經驗設計得到的輕量化結構。目前，拓撲優化已運用于航空航天、汽車工業、船舶設計、材料工程等應用領域。如空客A380機翼翼肋、福特汽車底盤結構、艦艇舷側防撞結構、衛星點陣夾層結構和智能材料等均采用了拓撲優化設計技術。持續增加的應用范圍驅動商用軟件巨頭們開發拓撲優化軟件或相關功能模塊，如Hyperworks、COMSOL、ANSYS、TOSCA等。根據拓撲優化方法及應用的研究現狀和工程需求，其未來發展趨勢在于如下方面：①方法的優化效率，即應用新理論、新技術降低優化方法的計算成本，提升方法的優化效果；②方法的穩定性，即減少優化迭代時的參數設置和約束選擇等人工干擾因素對優化結果的影響；③結構的可制造性，考慮增材制造工藝的現狀，使優化后的結構更加便于制造；④應用對象的擴展，即針對不同的優化問題如動力學、多物理場、材料設計、多尺度設計等。

1.2.2　多學科設計優化研究現狀

受各學科仿真需要花費龐大計算量、學科間信息交互耦合等因素的影響，計算復雜性和組織復雜性成為了MDO的兩大主要難點。在MDO領域眾多的研究方法中，近似模型和求解策略對有效降低MDO中計算復雜性和組織復雜性起到了非常重要的作用，這兩方面研究內容已經成為國內外學術界和工業界的研究熱點[3]。本節將對MDO中近似模型與求解策略的國內外研究現狀進行系統的綜述和討論。

1．近似模型研究現狀

20世紀80年代，Kleijnen[47]最早提出了近似模型的概念，他將近似模型稱為元模型（metamodel），即“a model of the model”，用于替代工程產品設計優化中昂貴耗時的計算機仿真程序，以降低計算量，減少計算時間和計算成本。20世紀90年代末期，Sobieszczanski-Sobieski和Haftka[48]總結了近似模型在MDO中的應用概況。2002年9月，在第9屆AIAA/USAF/NASA/ISSMO多學科分析與優化國際會議上，來自工業界和政府部門的研究學者重點討論了近似模型的研究與應用現狀，并指出了其未來的研究方向[49]。

目前，常用的近似模型主要包含以下幾種：響應面（response surface methodology，RSM）模型[50]、Kriging模型[51]、徑向基函數（radial basis functions，RBF）模型[52]，這3種模型在MDO中得到了廣泛應用。

1）響應面模型

RSM模型采用多項式回歸技術，利用最小二乘法對試驗數據進行擬合，得到輸出響應與輸入變量之間的近似函數關系，在工程產品多學科設計優化中應用廣泛。RSM模型具有構造簡單、易于操作的特點，能清楚地反映輸出響應與輸入變量之間的函數關系，深受廣大工程設計人員的喜愛。RSM模型比較適合于線性問題的近似，對于非線性問題，RSM模型往往表現出較低的近似精度[53]。

2）Kriging模型

Kriging模型起源于20世紀60年代，最初由南非采礦工程師Krige將其應用于地質統計學中進行空間估計。隨后，Matheron進一步發展了Kriging估計技術的數學意義[54]。20世紀80年代末期，Sacks等[51]將Kriging模型引入到工程領域，用于構建確定性計算機仿真中輸入與輸出數據之間的近似函數關系。從插值角度來講，Kriging是一種對空間分布的數據進行最優線性無偏估計的插值方法[51]，[55]。Kriging模型適用范圍廣，對于線性和非線性問題都具有較高的近似精度，在工程產品多學科設計優化中得到了廣泛的應用。但是Kriging模型的構建過程復雜，需要利用極大似然估計方法求解一個無約束的優化問題，而且Kriging模型無法直觀給出輸出響應與輸入變量之間的靈敏度信息[53]。

3）徑向基函數模型

RBF模型是一種多變量插值模型，是眾多神經網絡模型中的一種，它利用徑向基函數構造神經網絡的傳遞函數，不僅具有任意精度的泛函逼近能力，而且具有較快的收斂速度[52]，[56]。與Kriging近似模型相同，RBF模型也具有較廣的適用范圍，對于線性和非線性問題，RBF模型同樣也表現出了較好的近似精度，但是RBF模型也無法直觀反映輸入變量變化對輸出響應的影響程度[53]。

除了上述3種常用的近似模型外，還有其他一些近似模型也被應用到MDO中，如多元自適應回歸樣條（multivariate adaptive regression splines，MARS）模型[57]、人工神經網絡（artificial neural network，ANN）模型[58]、支持向量回歸（support vector regression，SVR）模型[59]和遺傳編程（genetic programming，GP）模型[60]，[61]等。每種近似模型都有其自身的優點和缺點，為總結各種近似模型的特點和適用范圍，國內外研究學者紛紛開始通過算例對它們的近似性能進行測試與比較。

國外關于近似模型比較的研究主要有：Giunta等[62]在超音速運輸機多學科設計優化的工程實例中，將RSM模型和Kriging模型進行對比分析，總結了它們各自的優缺點，并指出對于存在多個局部極值的響應數據，RSM模型的近似精度比較差，而Kriging模型則具有較高的近似精度。但是與RSM模型相比，Kriging模型的構建過程需要花費更多的計算量。Simpson等[63]，[64]將RSM模型和Kriging模型應用到飛行器塞式噴嘴設計中，對二者進行對比，得出Kriging模型近似精度較高的結論。Meckesheime等[65]通過對含有離散和連續變量的函數例子進行測試，對比了RSM模型、Kriging模型和RBF模型的近似精度，得出RBF模型的近似精度較好。Hussain等[66]利用全因子和拉丁超立方兩種試驗設計方法進行采樣，通過7個函數例子進行測試，比較得出RBF模型比RSM模型近似精度高。除此之外，國外還有一些關于近似模型比較的研究，具體可以參考文獻[67-69]。國內對近似模型比較的研究較少，主要以西北工業大學的張健和李為吉[70]為代表，他們將RSM模型、RBF模型、Kriging模型和增強的RBF模型進行對比分析，總結了4種近似模型的特點和適用范圍。

除了上述初步的比較研究外，國外少數研究學者對各種近似模型的性能進行了全面、系統的比較。Jin等[53]最早開展了此項研究工作，他們在考慮大、小和稀少3種樣本規模的基礎上，對非線性程度較高和較低的樣本數據、平滑與含數值噪聲的樣本數據進行近似預測，依據預測精度、魯棒性、計算效率、透明度和概念簡單性五種評價指標對RSM、Kriging、RBF和MARS4種近似模型進行了全面而系統的比較，總結了4種近似模型各自的優缺點和適用范圍。Clarke等[59]將SVR模型引入到近似模型領域中，從預測精度、魯棒性、計算效率和透明度4種評價指標出發，將SVR模型與MDO中常用的4種近似模型（即RSM、Kriging、RBF、MARS模型）進行對比，證明SVR模型具有潛在的廣闊應用前景。

目前，近似模型已經在工程產品設計優化中得到了廣泛應用，但是為了實現高精度近似，在構建近似模型前通常需要進行大規模的采樣。RSM模型具有透明度高、構建簡單的特點，比較適合于線性問題近似。Kriging和RBF模型能提供較高的近似精度，但是它們的透明度較差。在工程產品設計優化中，設計人員可以根據各個近似模型的特點和適用范圍，選擇合適的近似模型進行應用。

2．求解策略研究現狀

1）單級求解策略的研究現狀

在MDO發展初期，求解策略呈現單級形式，主要有多學科可行（multidisciplinary feasible，MDF，也稱為all-in-one，AIO）方法[71]、同時分析和設計（simultaneous analysis and design，SAND，也稱為all-at-once，AAO）方法[72]、單學科可行（individual discipline feasible，IDF）方法[73]。這些方法為求解早期簡單的MDO問題提供了有效的思路。

MDF方法通過系統分析模塊將各學科分析集中起來，在此基礎上利用優化算法對整個系統進行設計優化。該方法通過多學科系統分析來確保各學科間設計變量的一致性，整個系統只有一個優化器，是最早期的單級求解策略。AAO方法通過引入輔助設計變量來代替各學科分析狀態變量，從而避免了各個學科之間直接的耦合關系，使得各個學科能夠獨立并行地進行分析。輔助設計變量和各學科分析狀態變量之間的差異通過一致性約束來協調，最后執行系統優化，獲得MDO問題最優解。與AAO方法相同，IDF方法同樣也通過引入輔助設計變量的方式來實現各個學科的并行分析，但是AAO方法對所有學科分析的狀態變量都利用輔助設計變量來替代，IDF方法只是對各個學科之間的耦合狀態變量進行替代。與AAO方法相比，IDF方法能減少設計變量的數目，從而降低系統優化所需要的計算量。

上述3種單級求解策略通過學科分析與系統優化的集成，實現MDO問題的求解，求解系統中只存在一個優化器，整個優化過程需要進行大量的學科分析和系統分析，對于涉及學科較少、設計變量不多、計算量不大的工程產品MDO問題，往往能夠有效地獲得產品整體性能最優的設計方案。

2）多級求解策略的研究現狀

隨著結構、流體和控制等學科理論的不斷發展和完善，工程產品多學科設計優化中考慮到的學科因素越來越多，學科之間的耦合作用也越來越強。與此同時，計算機技術的飛速發展使得計算性能得到極大提高，有限元分析、計算流體動力學等仿真手段在工程產品設計中開始得到廣泛應用，設計人員從傳統的依靠經驗公式進行分析的方式中脫離出來，通過建立高精度仿真模型來進行學科分析。上述各種因素使得工程產品MDO需要進行更多昂貴耗時的學科分析和系統分析，單級求解策略已經不再適用。因此，各種多級求解策略開始紛紛涌現，主要包括：

（1）并行子空間優化（concurrent subspace optimization，CSSO）方法；該方法最早由Sobieszczanski-Sobieski[74]于1988年提出，是一種基于全局靈敏度方程（global sensitivity equation，GSE）近似的兩級求解策略。該方法根據各個學科分析與優化時所需變量的不同，將設計變量對應分配給各個學科或子空間，每個子空間獨立優化一組互不相交的設計變量。在各個子空間的優化過程中，對于該子空間的狀態變量，采用該子空間所屬學科的分析方法進行計算，對于其他子空間的狀態變量，則采用基于GSE的近似方法進行計算。各個子空間的優化結果構成一組設計方案，該方案作為CSSO方法下一次迭代的初始值。CSSO方法不僅降低了系統分析的次數，而且每個子空間可以獨立并行地進行設計優化，提高了優化效率。

（2）協同優化（collaborative optimization，CO）方法：Kroo等[75]于1994年在一致性約束優化方法的基礎上提出了CO方法，該方法將MDO問題分解為一個系統級和多個子系統級（或學科級）的設計優化問題，各個子系統在不考慮其他子系統設計約束的基礎上單獨進行設計優化，優化的目標是使子系統設計方案與系統級目標設計方案之間的差異最小。各個子系統優化結果的不一致性由系統級一致性約束進行協調，最后通過系統級優化與子系統級優化之間的多次循環迭代，得到一致性設計方案。

（3）兩級集成系統綜合（bi-level integrated system synthesis，BLISS）方法：該方法最早由Sobieszczanski-Sobieski等[76]于1998年提出，是一種基于GSE的兩級求解策略。該方法將設計變量劃分為系統級和學科級兩類，進而將原始的MDO問題分成系統級和多個子系統級優化問題。系統級優化與各個子系統級優化通過最優靈敏度導數信息相聯系，系統級和子系統級優化交替運行，從而獲得MDO問題整體最優解。BLISS方法的有效性取決于求解問題的非線性程度，對于非線性程度較低的問題，該方法可以有效地收斂到最優解，對于非線性程度很高或者非凸問題，該方法會隨著初始點選取的不同而得到不同的優化結果。

（4）分級目標傳遞（analytical target cascading，ATC）方法：ATC方法是Michelena等[77]于1999年提出的一種基于模型和層次優化的多級求解策略。它以工程產品的各個部件為標準將設計問題逐層分解為樹型結構，通過最小化樹型結構中層與層之間目標傳遞的偏差來獲得工程產品整體最優解。樹型結構中的節點稱為元素，元素由設計模型和分析模型組成，其中，設計模型通過調用分析模型來計算元素的響應。

3）多目標求解策略的研究現狀

工程產品多學科設計優化問題往往會涉及多個相互沖突的優化目標，目前對于求解多目標MDO問題的研究文獻不多，其思路主要體現在將傳統的多目標優化方法與現有的單目標MDO求解策略進行集成。Tappeta和Renaud[78]提出了多目標協同優化方法，該方法將多個目標進行線性加權轉換成單目標問題，然后利用CO方法來求解。Tappeta[79]在其博士學位論文中，對該方法進行了詳細的闡述與應用驗證。Huang[80]提出了多目標Pareto的并行子空間方法，其本質也是將多目標問題轉換成單目標問題，然后利用CSSO方法進行求解。McAllister等[81]將線性物理規劃與CO方法進行集成，用于多目標MDO問題的求解。陳剛等[82]提出了一種基于NSGA-Ⅱ算法的多目標協作優化方法。李連升等[83]將物理規劃與基于遺傳算法改進的CO方法進行集成，用于飛機起落架緩沖器的多目標多學科設計優化。

除了上述集成的方法外，基于博弈論（gametheory）的研究方法也被廣泛應用于多目標MDO問題的求解中。Rao[84]將合作博弈方法成功應用于結構多目標優化中。隨后，Rao等[85]利用合作博弈方法進行了結構與控制的一體化設計。Lewis和Mistree[86]總結了合作、非合作和領導／隨從3種博弈方式，用于描述工程產品多學科設計優化中3種不同的設計場景。Xiao等[87]利用博弈理論建立了學科設計小組之間的協同決策模型。張宏波等[88]將非合作博弈方法應用于汽車耐撞性多目標設計優化中，取得了比傳統的線性加權法更好的優化結果。趙健冬等[89]將非合作博弈方法應用于挖掘機工作裝置的多目標多學科設計優化中，證明了該方法的有效性。隨著工程產品復雜程度的提高，產品設計中考慮到的目標也會逐漸增多，如何快速準確地求解多目標MDO問題是研究的趨勢。

1.2.3　可靠性設計優化研究現狀

在開展可靠性設計優化時，根據結構的功能要求和相應的極限狀態標志，可建立結構的功能函數（performancefunction），也稱極限狀態函數（limitstate function）[90]：

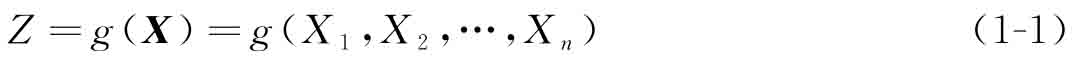
其中，X=(X₁，X₂，…，X_n)T表示不確定性隨機變量。通常定義Z>0表示結構可靠，Z<0表示結構失效，Z=0表示結構處于安全狀態，顯然Z=0表示的極限狀態邊界將整個空間分為可靠域Ω_r={X|g(X)>0}和失效域Ω_f={X|g(X)≤0}。可靠性分析是對當前設計點處的可靠度水平進行評估，根據當前設計點及其概率分布可以得到功能函數輸出響應不滿足設計要求的概率，即失效概率。考慮到設計點為連續的隨機變量，假設其聯合概率密度函數為f_X(X)，結構的失效概率可以表示為

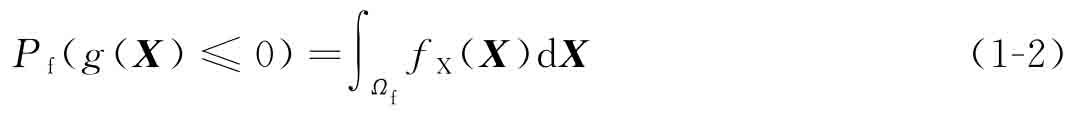
基于概率的可靠性設計優化模型如式（1-3）所示[91]，[92]：

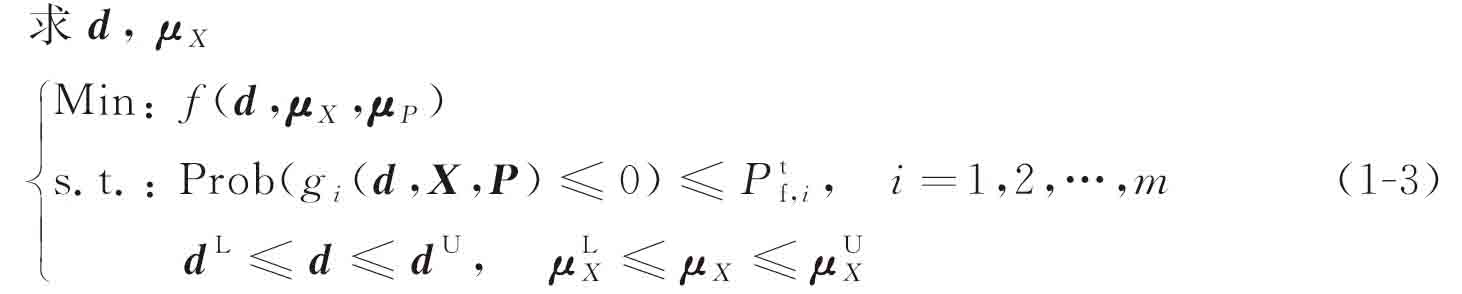
其中，d是確定性設計變量；X是隨機設計變量；P是隨機參數；μ_X和μ_P分別是X和P的均值。dL和dU分別是變量d的上下界， 和 分別是均值μ_X的上下界。f（d，μ_X，μ_P）表示目標函數，Prob（g_i（d，X，P）≤0）≤表示概率約束，i是概率約束的個數，概率約束表示為失效事件發生的概率應小于或等于許用失效概率（即最大失效概率）。

值得注意的是，式（1-3）的功能函數和式（1-2）的功能函數中的參數含義不同。在可靠性分析中，通常只有確定性變量和隨機變量，因為確定性變量不影響結構功能，所以式（1-2）中省略了確定性變量，只存在隨機變量。而在可靠性設計優化中，一般有設計對象——確定性變量d和隨機變量X（隨機分布的均值μ_X隨著設計進行不斷迭代更新），此外還存在隨機參數P（即隨機分布參數不變，相當于可靠性分析中定義的隨機變量）。從式（1-3）可以看出，可靠性設計優化分為兩個階段，分別是確定性優化階段和可靠性分析階段。當優化階段結束之后，輸出一個新的均值μ_X給隨機變量X。然后，隨機變量X攜帶新的分布參數和隨機參數P一起進行可靠性分析。因此式（1-3）中的可靠性分析和式（1-2）在原理上是一致的，只是為了和優化保持一致，才有了式（1-3）中的表達形式。本節將從可靠性分析與可靠性優化兩方面對RBDO的國內外研究現狀進行綜述。

1．可靠性分析研究現狀

可靠性分析即對式（1-3）中不等式概率約束的左半部分進行求解，該求解過程是一個不規則空間上的多維積分，如式（1-4）所示：

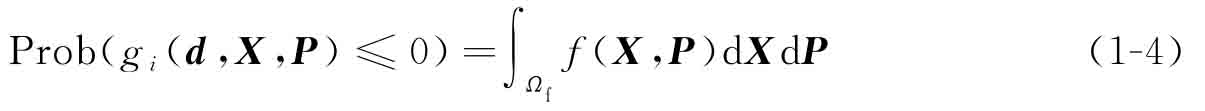
由于積分空間和積分表達式的復雜性，使得它的計算成本非常昂貴，有時甚至無法求解。并且，實際工程中功能函數的具體響應值需要借助有限元、計算流體動力學等計算成本昂貴的商用軟件才能得到。因此，在保證失效概率求解精度的前提下最大限度地減少功能函數響應的計算次數是可靠性分析領域的重要問題。目前已有的可靠性分析方法可以大致分為3類：①近似解析法；②仿真模擬法；③代理模型法。

1）近似解析法

近似解析法最早起源于1947年Freudenthal[93]提出的結構安全度概念，隨后，Cornell[94]于1969年提出了可靠性指標的概念，將結構響應的一階矩和二階矩與可靠度指標和失效概率進行對應。但當時的一次二階矩法（first-order second moment，FOSM）計算結果不具有唯一性，求解具有相同物理模型、不同形式的功能函數可能會得到不同的可靠度指標。直到1974年，Hasofer和Lind[95]給出了一個新的可靠度指標和相應的最大可能失效點（most probable point，MPP）概念：可靠度表示在獨立標準正態分布空間中坐標原點到極限狀態曲面的最小距離，而最小距離對應的點稱為MPP點。為了解決Hasofer-Lind方法僅能處理系統變量為正態分布的問題，Rackwitz和Flessler[96]于1978年提出了一種近似變換方法，建立了著名的HL-RF迭代方法，該方法成為國際結構安全聯合委員會推崇的標準算法。在HL-RF迭代方法的基礎上，相關學者又提出了一系列的改進方法。

經過近幾十年的發展，目前常用的方法主要有一次可靠性方法（first-order reliability method，FORM）和二次可靠性方法（second-order reliability method，SORM）。二者區別在于將功能函數在MPP點處進行一次或者二次Taylor展開，SORM由于能夠利用極限狀態函數在MPP點附近的曲率信息，從而比FORM更加精確。但SORM需要計算結構的Hessian矩陣，計算效率相對較低。此外，FORM和SORM只能處理獨立分布的隨機變量。因此，有關學者提出了許多變換方法，如Rosenblatt變換法[97]、正交變換法[98]、Nataf變換法[99]等。另一方面，FORM和SORM需要把非正態隨機變量轉換為正態分布隨機變量，這種轉換將增加功能函數的非線性，造成結果精度可能偏低。為了避免這種轉換，相關學者也提出了一系列的方法，此處不再贅述。

2）仿真模擬法

仿真模擬法的基本思想是根據隨機變量的統計分布規律按照一定策略隨機抽取樣本，進行大量的重復性試驗以獲得樣本點的響應，然后依據大數定律估計相應的失效概率[100]。其中，蒙特卡羅模擬法（Monte Carlo simulation，MCS）是可靠性分析中應用最廣的方法之一。理論上，MCS方法可以處理任何可靠性問題而不受變量維度和問題復雜度的影響，具有簡單精確、穩健性強的優點。但是MCS計算效率過低，尤其是對于單次計算成本較高問題和小失效概率問題，大量樣本點所花費的計算時間是難以接受的。由于MCS方法所求得結果非常精確，一般將其作為參考結果驗證其他方法的有效性。為了提高仿真模擬法的效率，有關學者提出了一些改進的仿真方法，如重要抽樣法（importance sampling，IS）、自適應重要抽樣法（adaptive importance sampling，AIS）、子集模擬法（subset simulation，SS）、線抽樣法（line sampling，LS）、方向抽樣法等。

重要抽樣法是一種最常見的改進仿真模擬法，具有抽樣效率高、計算方差小的優點。重要抽樣法把抽樣中心從隨機變量的均值點處移動到極限狀態函數上的驗算點，增加樣本點落入失效域的概率，從而提高抽樣效率和收斂速度。驗算點的獲取一般需要求解一個約束優化問題，有時多個驗算點不易求解，常規重要抽樣不太實用。于是有關學者還提出了一些自適應重要采樣法，如：基于核密度估計的自適應重要抽樣方法、基于模擬退火的自適應重要抽樣方法等。但是，重要抽樣法在處理高維問題和小失效概率問題時仍然面臨很大挑戰。有關學者提出了子集模擬法，它通過構造中間失效事件，將較小的失效概率轉化成一系列較大的條件失效概率的乘積。同時，使用馬爾科夫鏈MCS高效模擬條件樣本點來估計中間事件的失效概率，相對于MCS大大提升效率。線抽樣法是另一種處理高維小失效概率問題的有效方法，它在標準正態空間將一個高維抽樣問題轉化為多個一維的條件概率問題，從而實現了高效計算的目的。

3）代理模型法

對于復雜工程問題，功能函數通常表現為強非線性，甚至沒有顯示形式。因此利用有限的樣本信息建立結構輸入輸出的映射關系，并建立代理模型來代替計算昂貴的原始功能函數去預測未知樣本點的響應值。構建代理模型所需樣本點的數目直接關系到計算方法的效率，當代理模型構建完畢之后，即可使用仿真模擬法調用代理模型求得失效概率。

2．可靠性設計優化研究現狀

在可靠性設計優化中，當內部循環完成可靠性分析之后，外層循環接收可靠性分析結果，并進行新的外層確定性優化迭代。RBDO由于具有雙層結構，在求解過程中往往需要大量的迭代信息，這導致RBDO在實際運用中需要大量的計算成本。為提升RBDO效率，學者們提出了一系列新的求解思路。當前，可靠性設計優化方法主要分為兩類：①基于概率解析的RBDO方法；②基于近似模型的RBDO方法。

1）基于概率解析的RBDO方法

基于概率解析的RBDO方法主要包括兩類策略，一類是以序列優化和可靠度評估法[101](sequential optimization and reliability assessment，SORA)為代表的解耦策略，當然還有安全系數法[102](safety factor approach，SFA)、序列線性規劃法[103](sequential approximate programming，SAP)、直接解耦法[104](direct decoupling approach)、罰函數法[105](penalty-based approach)等。

以上解耦方法中，SORA因其操作簡單、求解穩定而被廣泛使用。在每個優化迭代步，SORA根據最可能失效點構建偏移向量，進而將確定性約束往概率約束處偏移，但SORA并不能保證該偏移向量完全精確，尤其是在優化初始階段。于是，筆者提出了最優偏移向量[106](optimal shifting vector，OSV)來提升SORA的解耦精度和效率。類似地，湖南大學姜潮等提出了增量偏移向量[107](incremental shifting vector，ISV)。此外，還有一些學者在SORA的基礎上發展了凸線性法[108](convex linearization，CL-SORA)、鞍點近似法[109](saddlepoint approximization)等。

另一類則是以單循環法[110]（single loopapproach，SLA）為代表的將內環可靠性分析轉接到外環概率約束當中的策略。單循環法結構簡單，具有很好的求解效率，但是單循環法只能處理線性或者輕度非線性問題。為了拓寬單循環法的應用，學者們做了一系列的嘗試。例如，Mansour等提出了響應面單循環法[111]（respon sesurface single loop，RSSL），該方法在確定性設計解附近構建確定性約束的二次響應面。Jeong等在單循環單向量法[112]（single loop single vector approach，SLSV）的基礎上引入了最可能失效點處的共軛梯度信息，進而處理單循環法迭代過程易陷入振蕩的缺點。類似地，合肥工業大學孟增等提出了混沌單循環法[113]（chaotic single loop，CSL）來進一步提升單循環法的計算穩定性。此外，單循環法由于依賴不完全精確的近似最可能失效點（most probable point，MPP）來消除內環可靠性分析，而導致其求解過程出現不規律振蕩現象。筆者針對這個問題，提出基于KKT條件的判斷準則，在優化迭代中自適應混合精確MPP和近似MPP[114]（adaptive hybrid single loop method，AH-SLM）。除了單循環法之外，具有單層優化結構的方法還包括可靠設計空間法[115]（reliable design space，RDS）、迭代可靠設計空間法[116]（iterative reliable design space，IRDS）等。

2）基于近似模型的RBDO方法

如前所述，近似模型技術在工程設計領域具有堅實的應用基礎和廣闊的應用前景。不同于解析方法主要致力于減少優化循環中可靠性分析的次數或者單次可靠性分析的迭代步數，基于近似模型的RBDO方法致力于用盡可能少的訓練點構建足夠精確的近似模型來代替原始功能函數。此類方法一般選擇仿真模擬法進行可靠性分析，選擇梯度優化方法或者元啟發式算法進行優化。

基于近似模型的RBDO方法有兩類建模策略：①設計域全局建模（global surrogate modeling）策略；②設計驅動的局部建模（design-drived local surrogate modeling）策略。設計域全局建模策略即在最優解可能出現的區域建立精度達標的近似模型，通常有一次采樣和序列采樣兩種方式。當近似模型達到預定精度之后，再基于該模型進行全局優化。而設計驅動的局部建模策略則在每一迭代步的當前優化解附近采樣，采樣建模和優化序列進行，直至找到最優解。

盡管以上提到的近似模型都可以運用于RBDO中，但支持向量回歸模型和Kriging模型的應用相對更加廣泛。其中，支持向量回歸模型具有天然的分類能力，而Kriging模型能夠提供預測局域的不確定性。在支持向量回歸模型方面，Hurtado[117]將統計學習理論引入可靠性領域，建立極限狀態函數的近似模型，對預測響應進行分類。Missoum等[118-121]則在2007年至2015年間，用支持向量機模型擬合可靠性分析的決策邊界，提出一系列函數識別、自適應采樣和支持向量機參數選擇的策略來處理非連續響應和多失效域問題。此外，Choi等[122]還提出了用于RBDO的虛擬支持向量機。在Kriging模型方面，Choi等[123]，[124]提出動態Kriging模型進行概率分析，同時還提出了變量篩選方法和模型不確定性量化策略[125]，進一步增強了近似模型在可靠性設計優化中的可行性。本書作者充分融合Kriging模型和RBDO的特點，提出了基于目標函數特性、當前最可能失效點的局部自適應更新方法[126]，[127]，此外，本書作者還提出了變可信度建模框架來適應工程需求[128]。