- 優(yōu)化驅(qū)動的設(shè)計方法
- 高亮 邱浩波 肖蜜 李好
- 4676字
- 2021-12-10 16:41:14
2.1 參數(shù)化水平集方法
2.1.1 基于水平集的結(jié)構(gòu)邊界隱式表達
基于水平集的結(jié)構(gòu)邊界隱式表達的思想是將結(jié)構(gòu)邊界隱式地嵌入到高一維的水平集函數(shù)中,并將結(jié)構(gòu)邊界視為水平集函數(shù)的零等值面,如圖2-1所示。值得注意的是,這里的水平集函數(shù)應(yīng)具有Lipschitz連續(xù)性[5],[6]。假定有一個固定的歐拉空間作為參考設(shè)計域D,該設(shè)計域中包含了實體、邊界和孔洞,設(shè)計域D中的各個部分可按照如下方式進行數(shù)學(xué)表達:
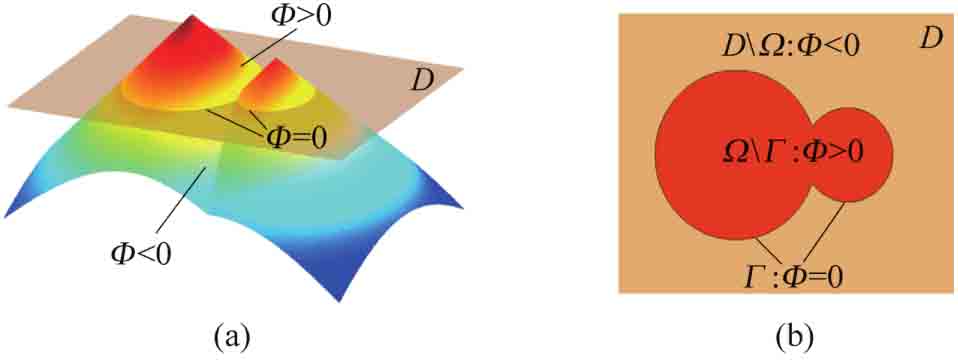
圖2-1 結(jié)構(gòu)邊界及其對應(yīng)的水平集函數(shù)

其中,x代表設(shè)計域D中的空間變量,即水平集網(wǎng)格的坐標;t為一種虛擬的時間變量;Ω表示設(shè)計域中結(jié)構(gòu)的所有可能形狀;Γ代表結(jié)構(gòu)邊界。需要注意的是Γ包含了Dirichlet邊界ΓD、Neumann邊界ΓN和無牽引力邊界ΓF:

除了將結(jié)構(gòu)邊界表述為零水平集外,基于水平集的結(jié)構(gòu)邊界隱式描述的另外一個重要問題是將結(jié)構(gòu)邊界幾何信息映射到力學(xué)模型中。一般地,結(jié)構(gòu)邊界的數(shù)學(xué)表達式(2-1)可重新表達為一種包含Heaviside函數(shù)H(Φ)的格式。例如,可利用H(Φ)在結(jié)構(gòu)設(shè)計域內(nèi)構(gòu)建泛函J的積分形式:
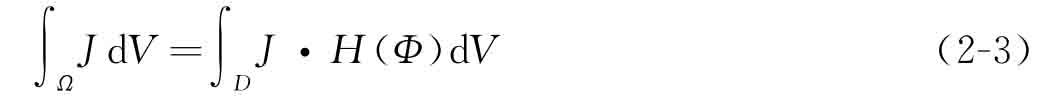
其中

式(2-3)中,dV代表體積積分。
在進行結(jié)構(gòu)拓撲優(yōu)化設(shè)計時,式(2-3)可以通過有限元方法在固定網(wǎng)格上進行近似計算。然而在水平集方法中,若不重新劃分網(wǎng)格,標準的有限元方法很難準確地計算一些結(jié)構(gòu)邊界上的單元應(yīng)變,特別是當(dāng)固定的有限單元被動態(tài)的水平集邊界所分割時,固定有限元網(wǎng)格所帶來的計算誤差會更大[7],[8]。學(xué)者們通常會采用一種所謂的人工材料模型[8],[9]來應(yīng)對上述問題。該模型假設(shè)有限單元的應(yīng)變或剛度等指標與該單元的材料百分比(即虛擬單元密度)成正比,且孔洞單元由一種密度極低的弱材料填充以避免剛度矩陣奇異。在該假設(shè)的基礎(chǔ)上,泛函J的體積積分可由有限元法近似計算得到:
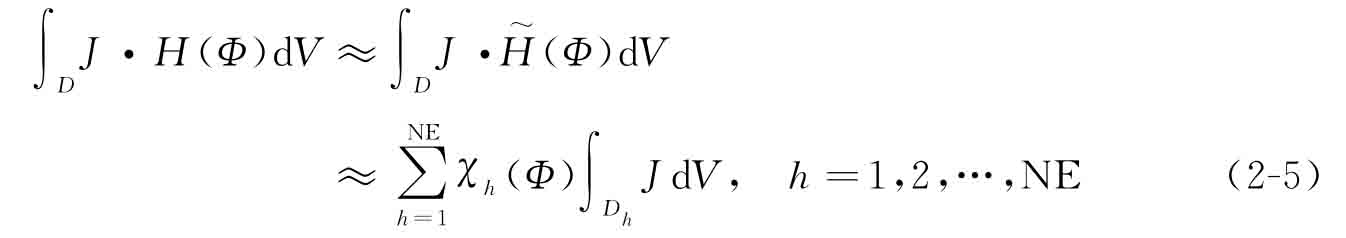
其中,h表示設(shè)計域D中的任一單元;Dh表示該單元的設(shè)計空間;NE代表有限單元的數(shù)量。由于精確的Heaviside函數(shù)式(2-4)不可微,在拓撲優(yōu)化設(shè)計過程中需要引入一種近似的Heaviside函數(shù)(光滑且可微)[9]來替代精確的Heaviside函數(shù):
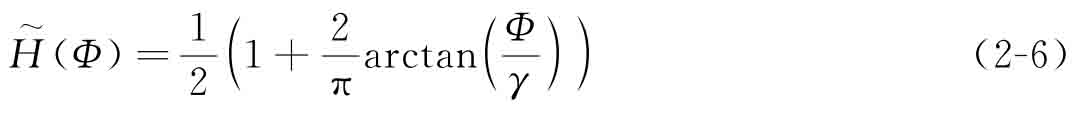
近似Heaviside函數(shù)的偏導(dǎo)數(shù),即Dirac delta函數(shù)可定義為
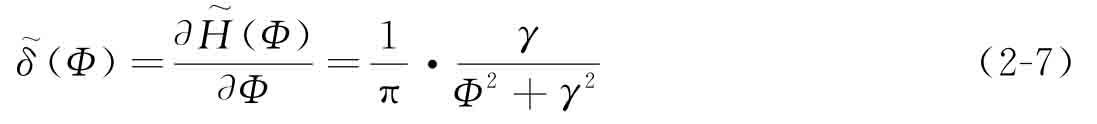
在式(2-6)和式(2-7)中,γ是一個足夠小的正數(shù),其大小通常等于2Δ,Δ代表固定水平集網(wǎng)格的邊長。于是,前面提到的虛擬單元密度可被定義為
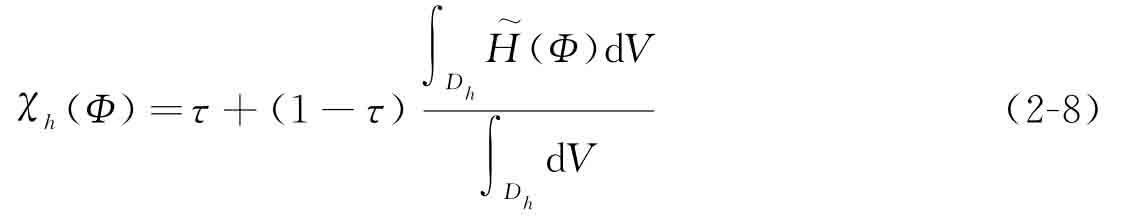
其中,τ=0.001被用于避免計算奇異問題。式(2-8)中,位于空間Dh上的體積積分可通過高斯積分法進行計算。值得注意的是,對于結(jié)構(gòu)邊界上的單元,需要布置大量的高斯積分點來保證計算精度[9]。類似地,下面的體積積分亦可由有限元方法近似計算得到:
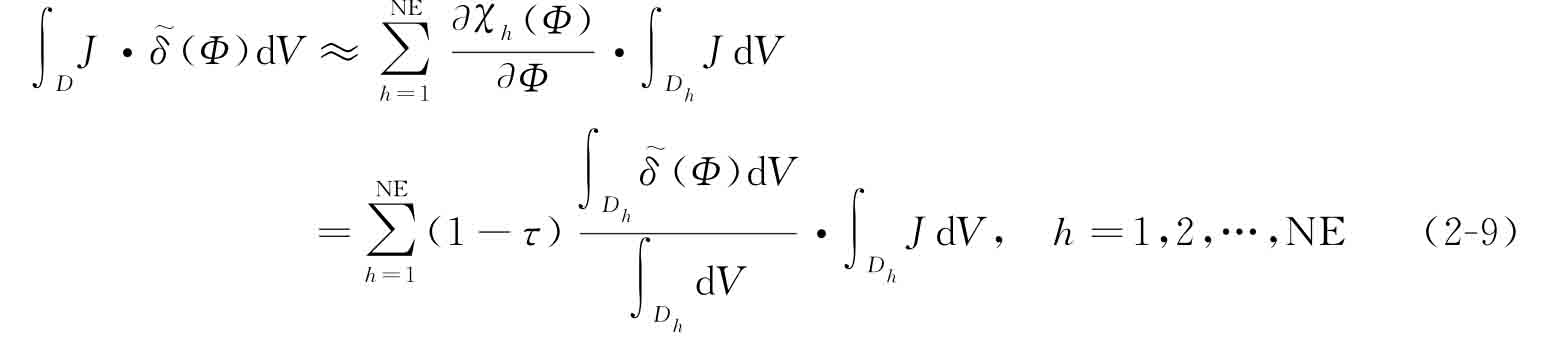
通過引入時間變量t,水平集函數(shù)隨時間沿特定方向動態(tài)變化從而實現(xiàn)結(jié)構(gòu)的拓撲優(yōu)化。利用鏈式求導(dǎo)法則對水平集函數(shù)Φ(x,t)=0求其關(guān)于時間變量t的偏導(dǎo)[10],可得Hamilton-Jacobi偏微分方程,如下所示:
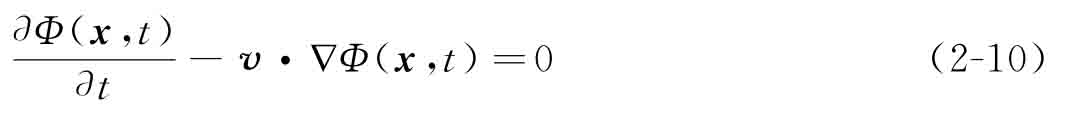
其中,v=dx/dt為結(jié)構(gòu)邊界上的速度場。v由法向速度場和切向速度場構(gòu)成,由于僅法向速度對結(jié)構(gòu)邊界的形狀演化起作用[11],[12],故式(2-10)可改寫為
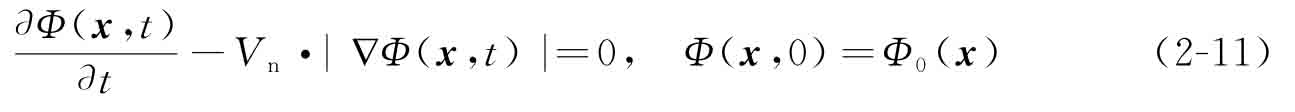
其中法向速度為
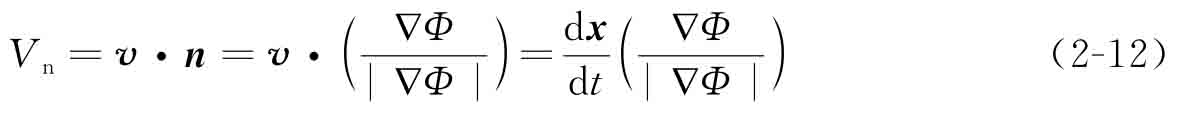
在水平集方法的框架下,水平集函數(shù)并沒有一種顯式的解析形式,因此水平集在優(yōu)化過程中的運動必須通過求解Hamilton-Jacobi偏微分方程來實現(xiàn)。結(jié)構(gòu)邊界的優(yōu)化過程可等價于在速度場驅(qū)動下的水平集面的演化過程,而該速度場由給定的目標函數(shù)和約束條件所決定。通過Hamilton-Jacobi偏微分方程求解合適的速度場十分困難,通常需用規(guī)則的網(wǎng)格將水平集函數(shù)離散化,并采用差分方法求解,例如基于Eulerian方法的顯式有限差分[11],[13]。運用有限差分方法時需謹慎處理其數(shù)值計算問題,例如速度場的擴展(velocity extension)、重新初始化(re-initialization)以及CFL條件(CFLcondition)等[14]。這些復(fù)雜的數(shù)值計算過程導(dǎo)致水平集方法的效率和穩(wěn)定性下降,阻礙其在結(jié)構(gòu)優(yōu)化領(lǐng)域的發(fā)展和應(yīng)用。為克服上述數(shù)值計算困難,并提高求解效率,下文將在傳統(tǒng)水平集方法的基礎(chǔ)上,討論一種基于CSRBF和離散小波變換(discrete wavelet transform,DWT)的參數(shù)化水平集方法。
2.1.2 基于徑向基函數(shù)插值的水平集函數(shù)參數(shù)化
徑向基函數(shù)(radial basis function,RBF)的特點是能夠利用一元函數(shù)來描述多元函數(shù),其最為常見的應(yīng)用場景是用于近似或者擬合大規(guī)模散亂數(shù)據(jù)的幾何形狀。徑向基函數(shù)運算簡單、存儲方便及計算效率高,在學(xué)術(shù)界和工程界得到了非常廣泛的關(guān)注和應(yīng)用。理論上,當(dāng)非線性等式在插值節(jié)點處構(gòu)成的插值矩陣可逆時,RBF可確保近似曲面或超曲面的光滑性。因此與水平集方法結(jié)合,RBF能夠快捷地逼近任何可能的形狀與拓撲,同時保留水平集方法隱式邊界描述的優(yōu)點[13],[15]。RBF方法的一些獨特優(yōu)點,例如插值系統(tǒng)解的唯一性、插值計算的效率、RBF的光滑性和收斂性等,使該方法在拓撲優(yōu)化領(lǐng)域的應(yīng)用很有吸引力[16]。
利用具有N個插值點的一組RBF,任意函數(shù)f(x):Rd→R(d≥1)的近似形式可定義為
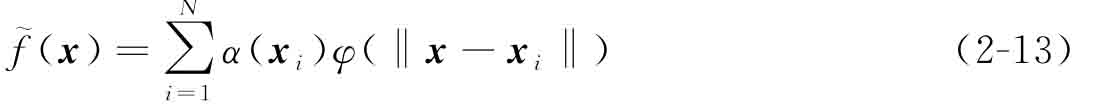
其中,xi為第i個插值控制點的位置坐標;α為插值擴展系數(shù);φ為徑向基函數(shù);‖·‖代表d維空間上的歐氏距離。
RBF插值的精度與效率很大程度上由所選取的插值核函數(shù)決定,按照插值過程中形成矩陣的稀疏性來區(qū)分,可將RBF分為全局支撐的徑向基函數(shù)(GSRBF)和緊支撐徑向基函數(shù)(CSRBF)兩類[17]。GSRBF具有精度高、光滑性好的特點,但其在近似水平集面的過程中會產(chǎn)生元素全部非零的插值矩陣,導(dǎo)致計算復(fù)雜度達到O(N2)甚至O(N3)[18],難以適應(yīng)大規(guī)模結(jié)構(gòu)優(yōu)化問題。此外,GSRBF插值精度很大程度上取決于所謂的自由形狀參數(shù)(free shape parameter),目前并沒有可靠的方法來確定不同拓撲優(yōu)化問題中自由形狀參數(shù)的取值。相比之下,CSRBF具有嚴格正定、插值系數(shù)矩陣稀疏、參數(shù)對全局計算精度影響小,以及插值操作能夠繼承CSRBF的連續(xù)性等優(yōu)點,使其更加適合結(jié)構(gòu)拓撲優(yōu)化問題。雖然CSRBF插值精度稍低于GSRBF,但針對常見的拓撲優(yōu)化設(shè)計問題,兩類基函數(shù)均能夠滿足水平集方法的精度要求。
本書將采用CSRBF對水平集函數(shù)進行插值,以此將水平集方法轉(zhuǎn)化為一種廣義的參數(shù)化形式。Wendland[19]所提出的系列CSRBF可表示為

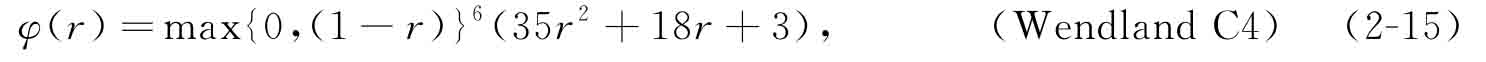
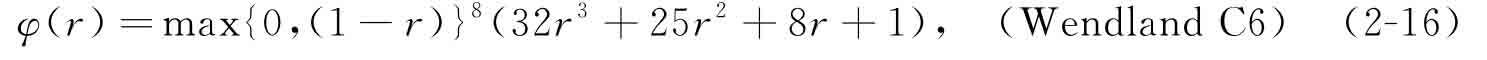
對于二維問題,r為定義在歐式空間內(nèi)的支撐半徑(radiusof support):
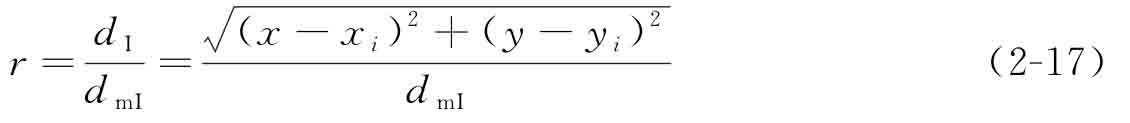
其中,dI表示在CSRBF的支撐半徑范圍內(nèi),當(dāng)前樣本點(x,y)到插值控制節(jié)點(xi,yi)間的距離。dmI反映CSRBF在節(jié)點(xi,yi)處的影響范圍大小。要保證插值的穩(wěn)定性和效率,需要選擇大小合適的支撐半徑,過小的支撐半徑會導(dǎo)致插值奇異,過大的支撐半徑顯著增加計算成本。在本書中采用文獻[20,21]給出的支撐半徑:令參數(shù)dmI=dmax×CI,其中尺度因子dmax取值為2.0~4.0,CI決定當(dāng)前插值控制點的鄰域范圍,以保證在鄰域內(nèi)搜索到足夠多的控制點。
圖2-2對比了具有C2階、C4階和C6階連續(xù)性CSRBF的形狀。可見,不同階的CSRBF均具有良好的光滑性,表明若空間內(nèi)插值點布置合理,3種CSRBF都能夠很好地對水平集函數(shù)進行逼近,并保證插值所得函數(shù)的光滑性和完備性。
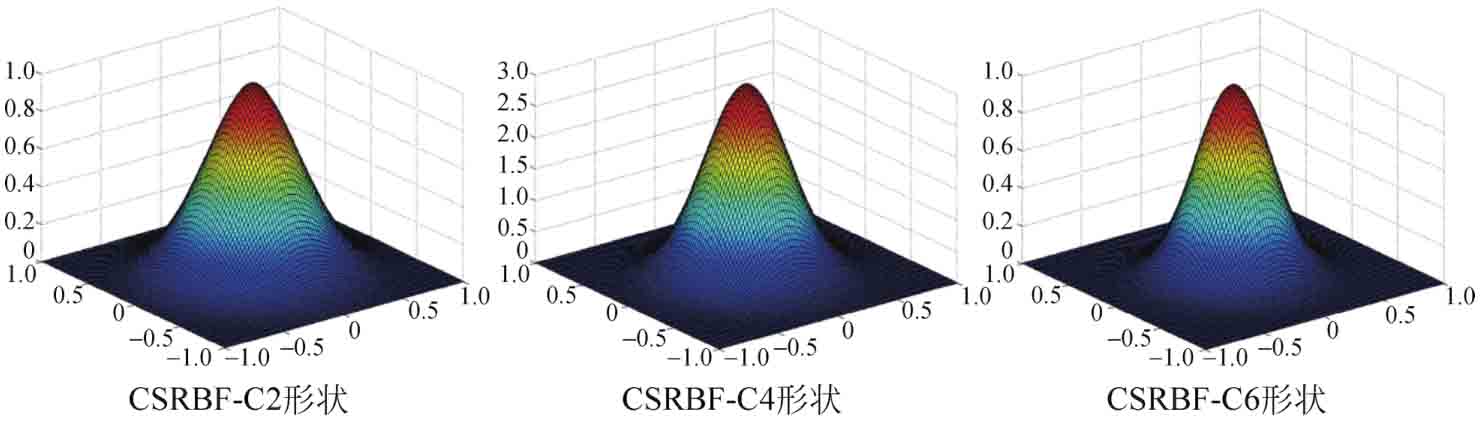
圖2-2 不同連續(xù)性CSRBF的形狀對比
利用CSRBF插值,水平集函數(shù)可被近似表達為一組CSRBF與其擴展系數(shù)的乘積形式:
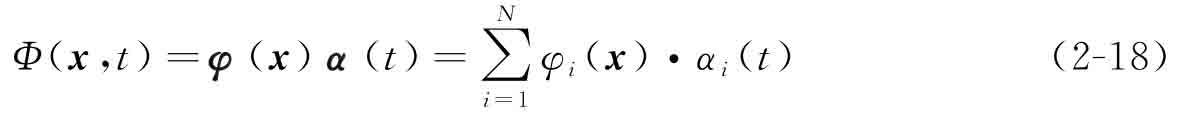
其中,α(t)=[α1(t),α2(t),…,αN(t)]T為CSRBF插值的擴展系數(shù),φ(x)=[φ1(x),φ2(x),…,φN(x)]包含了全部的CSRBF。可見,CSRBF僅與空間變量相關(guān),擴展系數(shù)僅與時間變量相關(guān),水平集函數(shù)則實現(xiàn)了時空變量解耦。Gaussian RBF通過考慮設(shè)計域內(nèi)的全部插值點信息來獲取當(dāng)前樣本點的水平集函數(shù)值,因此具有極高的插值精度,但這也勢必將帶來高昂的計算成本。為方便論述,現(xiàn)將式(2-18)改寫為如下矩陣運算形式:
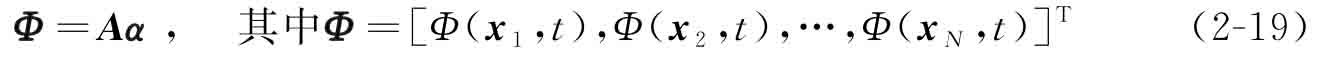
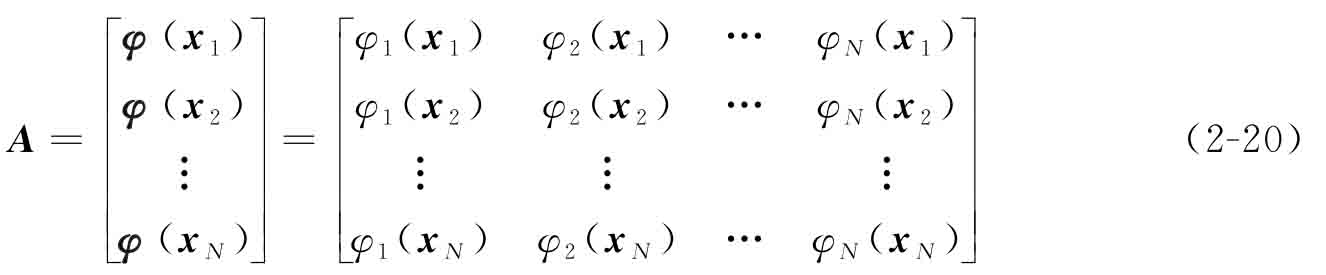
其中,A為可逆矩陣。不難發(fā)現(xiàn),A的稀疏性對插值效率有重要影響。
將式(2-18)代入到經(jīng)典的Hamilton-Jacobi偏微分方程中[7],可將該偏微分方程轉(zhuǎn)化為一系列易解的常微分方程:
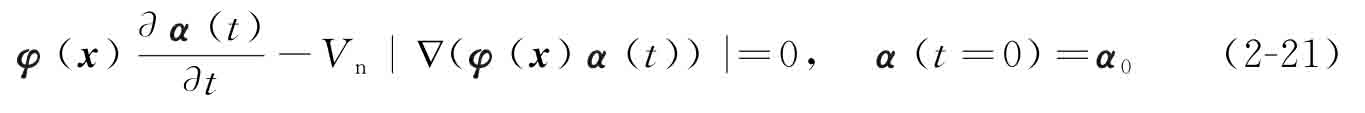
其中,α0代表在時間t=0時的擴展系數(shù)向量,可以在初始迭代階段通過求解式(2-19)計算獲得。于是,水平集的速度場Vn可進一步表示為
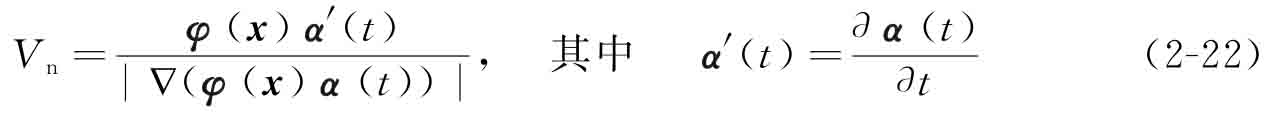
至此,標準的水平集方法被轉(zhuǎn)化為一種參數(shù)化形式,能夠在保持傳統(tǒng)水平集方法有點的基礎(chǔ)上,克服其應(yīng)用缺陷。通過式(2-22)可知,速度場Vn在設(shè)計域內(nèi)的全部節(jié)點上進行計算,說明水平集的速度場被自然地擴展到了整個設(shè)計域上,從而無需額外引入所謂的速度擴展策略[22]。由于Hamilton-Jacobi偏微分方程被轉(zhuǎn)化為常微分方程,水平集函數(shù)的更新也不再受限于CFL條件[23],優(yōu)化效率將被顯著提升。此外,此時的設(shè)計變量不再是水平集函數(shù),而是CSRBF插值的擴展系數(shù),表明結(jié)構(gòu)拓撲優(yōu)化設(shè)計問題被簡化為一種廣義的“尺寸”優(yōu)化問題,而該問題能夠被高效的梯度型算法[24],[25]求解,這將進一步提升水平集方法的適用性。
2.1.3 基于離散小波分解的插值矩陣壓縮技術(shù)
面對復(fù)雜的大規(guī)模優(yōu)化問題,基于CSRBF的參數(shù)化水平集法的計算效率雖然由于插值矩陣A的稀疏性得到了一定提高,但其具備進一步提升的空間[16]。本章引入離散小波變換(discrete wavelet transform,DWT)技術(shù)對由CSRBF構(gòu)建的插值矩陣A進行再壓縮,從而獲得一種極其稀疏的插值系統(tǒng),減少優(yōu)化過程的處理時間及其所需的計算機存儲空間。
DWT是一種輸入信號或信息的多分辨率分解技術(shù),近幾十年來被廣泛用于信號處理(signal processing)、圖像壓縮(image gompression)、去噪(denoising)等方面[26]。因其具備利用極少元素捕獲大規(guī)模信息集合中關(guān)鍵信息的能力,使DWT的應(yīng)用范圍得以擴展到大規(guī)模線性系統(tǒng)或方程組中矩陣和向量的壓縮[27],[28]。若將式(2-19)給出的水平集函數(shù)插值操作視為規(guī)模與插值控制節(jié)點數(shù)量相關(guān)的線性系統(tǒng),那么基于DWT的矩陣壓縮技術(shù)則可作為一種“黑箱”操作嵌入到參數(shù)化水平集模型中,這意味著能在不改變參數(shù)化水平集模型的前提下,通過增加幾次代價較小的小波變換,即可起到減少插值計算成本的效果。簡言之,DWT能夠在幾乎不損失計算精度的前提下將稠密插值矩陣壓縮為一種極其稀疏的矩陣。
針對式(2-19)中的水平集函數(shù)插值矩陣A,DWT首先將其轉(zhuǎn)化為相同規(guī)模的小波基矩陣  。依據(jù)該小波基矩陣
。依據(jù)該小波基矩陣  的數(shù)據(jù)分布,能夠分辨出其中的關(guān)鍵元素和噪聲元素。因此,接下來可以通過閾值過濾技術(shù),清除掉
的數(shù)據(jù)分布,能夠分辨出其中的關(guān)鍵元素和噪聲元素。因此,接下來可以通過閾值過濾技術(shù),清除掉  中相當(dāng)部分的無用元素,從而構(gòu)建一個極其稀疏的新矩陣
中相當(dāng)部分的無用元素,從而構(gòu)建一個極其稀疏的新矩陣  s。最終,水平集函數(shù)能夠通過該稀疏矩陣
s。最終,水平集函數(shù)能夠通過該稀疏矩陣  s計算得到。
s計算得到。
其中,α(0)表示原始向量α中的任一元素。  和
和  均為小波變換后的新向量
均為小波變換后的新向量  中的元素,其中k=1,2,…,N/2。需要注意的是,為保證一級小波變換具備完整的小波階,通常需要向量的長度N為偶數(shù)。若N為奇數(shù),可采用一種簡易的處理方式,即在小波變化過程中在原始向量α中額外增加一項“0”元素,在重構(gòu)原始向量α時再去除掉額外增加的一項“0”元素。[h1,h2]=[
中的元素,其中k=1,2,…,N/2。需要注意的是,為保證一級小波變換具備完整的小波階,通常需要向量的長度N為偶數(shù)。若N為奇數(shù),可采用一種簡易的處理方式,即在小波變化過程中在原始向量α中額外增加一項“0”元素,在重構(gòu)原始向量α時再去除掉額外增加的一項“0”元素。[h1,h2]=[  /2,
/2,  /2]為高通濾波器,[g1,g2]=[-
/2]為高通濾波器,[g1,g2]=[-  /2,
/2,  /2]為低通濾波器[29]。二維插值矩陣A的分解過程本質(zhì)上為多次一維DWT過程的疊加。典型的二維分解過程如圖2-3所示[26-30]。為方便論述,引入N×N卷積矩陣W[31]描述該塔式算法:
/2]為低通濾波器[29]。二維插值矩陣A的分解過程本質(zhì)上為多次一維DWT過程的疊加。典型的二維分解過程如圖2-3所示[26-30]。為方便論述,引入N×N卷積矩陣W[31]描述該塔式算法:
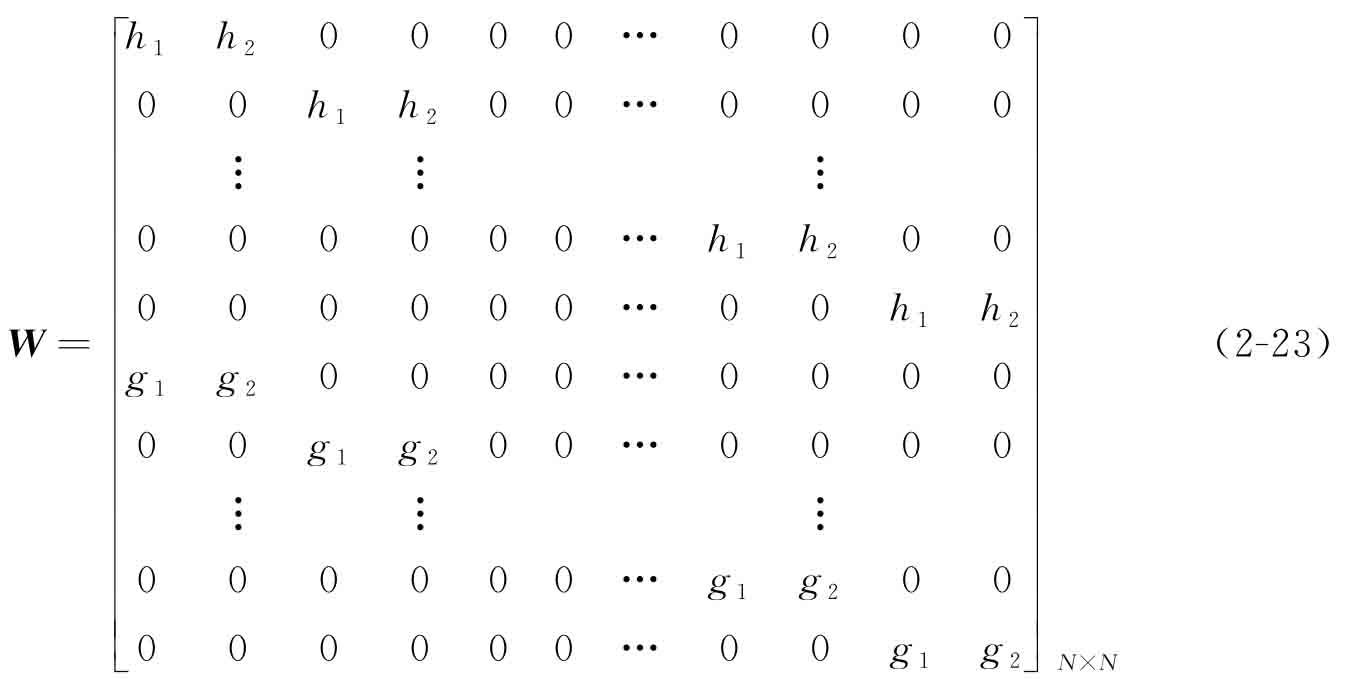
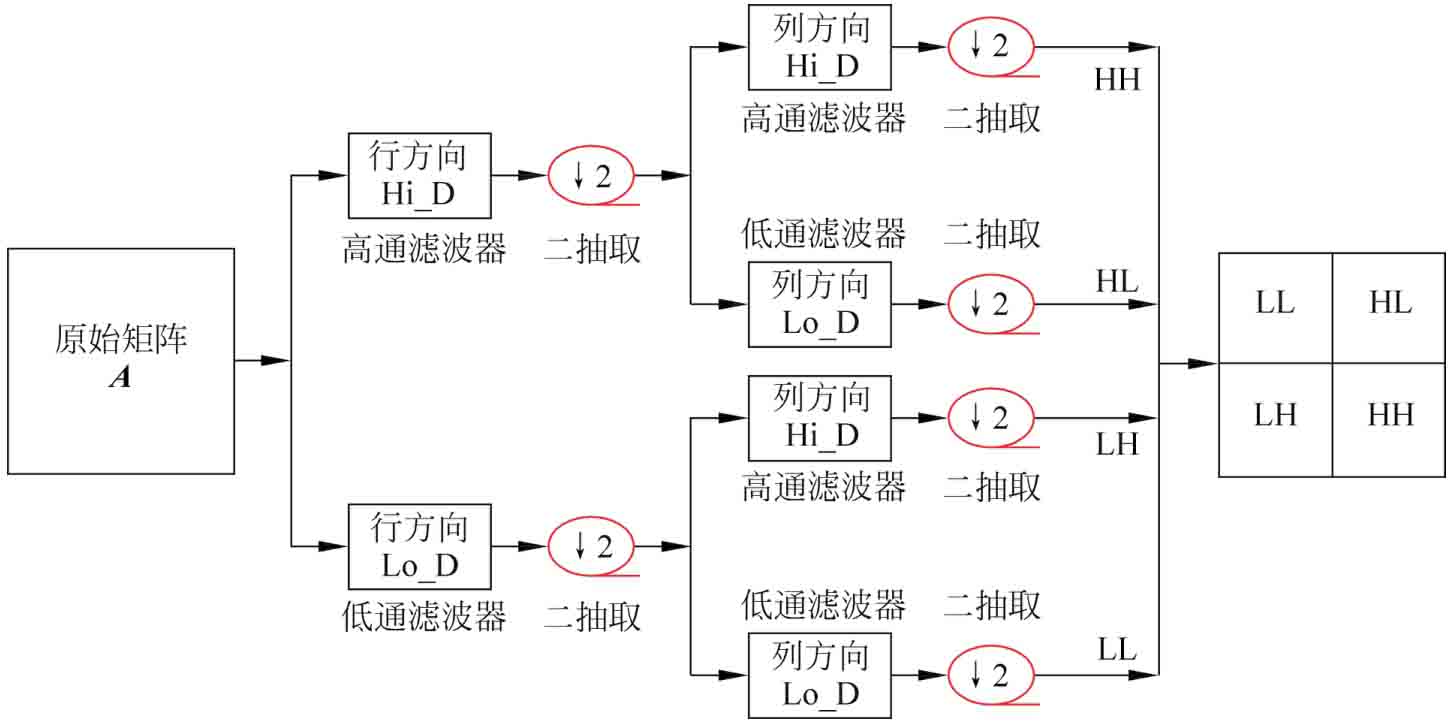
圖2-3 采用一級分解的二維離散小波變換過程
由式(2-23)可以看出,W為正交矩陣。利用該W矩陣,經(jīng)小波變換后的水平集函數(shù)  、擴展系數(shù)向量
、擴展系數(shù)向量  和插值矩陣
和插值矩陣  可分別表達為
可分別表達為


在式(2-19)兩端分別左乘W可得

其中,WT與W為單位矩陣。
通過比較式(2-24)~式(2-26)可以得到新的插值系統(tǒng):

接下來,利用下述閾值過濾算法來去除小波基矩陣  中的無用元素,從而構(gòu)建極其稀疏的插值矩陣
中的無用元素,從而構(gòu)建極其稀疏的插值矩陣  s:
s:
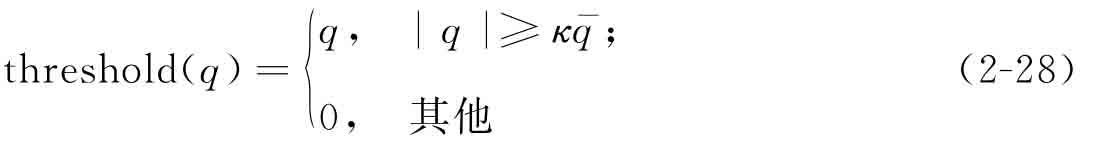
其中,q為矩陣  中的任意元素;
中的任意元素;  為矩陣
為矩陣  中全部元素的平均絕對值;κ為閾值調(diào)整參數(shù)。經(jīng)過閾值過濾后,可以將式(2-27)的插值過程重建為一種極其稀疏的插值系統(tǒng):
中全部元素的平均絕對值;κ為閾值調(diào)整參數(shù)。經(jīng)過閾值過濾后,可以將式(2-27)的插值過程重建為一種極其稀疏的插值系統(tǒng):

下面簡述引入DWT后的優(yōu)化過程。特別地,在第一次迭代中,將t=0時的水平集函數(shù)記為Φ0,其小波變換后的形式記為  ,式(2-21)中定義的初始擴展系數(shù)向量α0可由逆過程
,式(2-21)中定義的初始擴展系數(shù)向量α0可由逆過程  計算得出。而α0的小波變換形式
計算得出。而α0的小波變換形式  0則可由
0則可由  計算得到。在后續(xù)迭代中,首先可利用基于梯度的優(yōu)化算法更新設(shè)計變量α。接著可通過式(2-24)計算獲得
計算得到。在后續(xù)迭代中,首先可利用基于梯度的優(yōu)化算法更新設(shè)計變量α。接著可通過式(2-24)計算獲得  ,并通過式(2-29)更新水平集函數(shù)的小波基形式
,并通過式(2-29)更新水平集函數(shù)的小波基形式  。最后,通過重構(gòu)過程
。最后,通過重構(gòu)過程  得到水平集函數(shù)的原始基形式。
得到水平集函數(shù)的原始基形式。
如上所述,本章將DWT與CSRBF結(jié)合起來構(gòu)建了一種新的參數(shù)化水平集方法以提高求解大規(guī)模優(yōu)化問題時的計算效率。與基于CSRBF的參數(shù)化水平集方法相比,上述方法在插值矩陣中含有更多零元素,求解更快速。值得指出的是,在上述方法中稀疏的插值矩陣  s僅需在整個優(yōu)化過程中計算一次。可見,上述參數(shù)化水平集方法僅僅是在插值過程中增加了一次小波變換操作
s僅需在整個優(yōu)化過程中計算一次。可見,上述參數(shù)化水平集方法僅僅是在插值過程中增加了一次小波變換操作  =W α和一次重構(gòu)操作
=W α和一次重構(gòu)操作  ,而這兩個操作均利用極其稀疏的矩陣W,因此該過程所帶來的額外計算成本可以忽略不計。
,而這兩個操作均利用極其稀疏的矩陣W,因此該過程所帶來的額外計算成本可以忽略不計。
- JavaScript修煉之道
- LabVIEW Graphical Programming Cookbook
- PaaS程序設(shè)計
- 樂高機器人設(shè)計技巧:EV3結(jié)構(gòu)設(shè)計與編程指導(dǎo)
- ASP.NET Core 2 Fundamentals
- OpenCV with Python Blueprints
- Python 3快速入門與實戰(zhàn)
- Go Systems Programming
- 基于JavaScript的WebGIS開發(fā)
- micro:bit軟件指南
- PHP程序設(shè)計高級教程
- 計算機輔助設(shè)計與繪圖技術(shù)(AutoCAD 2014教程)(第三版)
- 精通Rust(第2版)
- 信息學(xué)競賽寶典:基礎(chǔ)算法
- 瘋狂Java講義精粹