- 2D 計算機視覺:原理、算法及應用
- 章毓晉編著
- 1111字
- 2021-10-29 23:40:40
4.2 頻域低通濾波器
低通濾波器的功能是削弱或消除高頻分量而保留低頻分量。
4.2.1 理想低通濾波器
一個2D理想低通濾波器的轉移函數滿足下列條件:
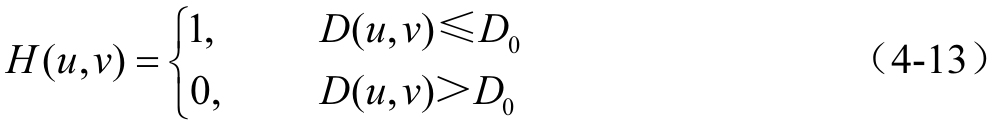
其中,D0是非負整數;D(u, v)是點(u, v)到頻率平面原點的距離,D(u, v)=(u2+v2)1/2。
圖4-4(a)給出H(u,v)的剖面圖(設D關于原點對稱),圖4-4(b)給出H(u,v)的透視圖。這里的“理想”是指小于或等于D0的頻率可以完全不受影響地通過濾波器,而大于D0的頻率則完全通不過,因此D0也被稱為截斷頻率。盡管理想低通濾波器在數學上的定義很明確,在計算機模擬中也可實現,但在截斷頻率處直上直下的理想低通濾波器是無法用實際的電子器件實現的。
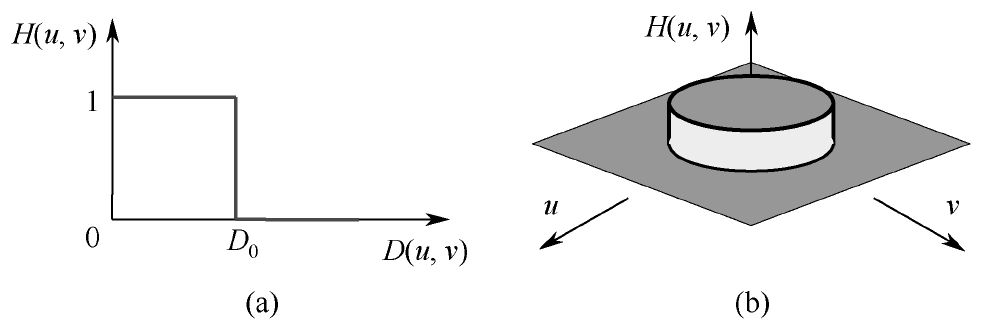
圖4-4 理想低通濾波器轉移函數剖面圖和透視圖
例4-3 頻域低通濾波與圖像能量
圖4-5(a)為圖1-5(a)的傅里葉頻譜,其上疊加的4個圓周的半徑分別為5、11、45和68。這些圓周內分別包含了原始圖像90%、95%、99%和99.5%的能量。若用R表示圓周半徑,B表示圓周內(濾波后保留)的圖像能量百分比,則有
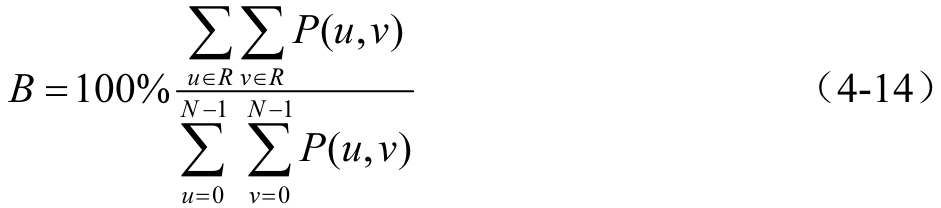
其中,P(u, v)是f(x, y)的傅里葉頻譜的功率譜。圖4-5(b)~圖4-5(e)分別為用由以上各圓周半徑確定的截斷頻率對應的理想頻域低通濾波器進行處理的結果。

圖4-5 理想頻域低通濾波的處理結果
由圖4-5(b)可見,盡管只有10%的(高頻)能量被濾除,但圖像中絕大多數細節信息都已丟失,事實上這幅圖像已無多少實際用途。由圖4-5(c)可見,當僅5%的(高頻)能量被濾除時,圖像中仍有明顯的振鈴效應。由圖4-5(d)可見,如果只濾除1%的(高頻)能量,圖像雖有一定程度的模糊,但視覺效果尚可。最后由圖4-5(e)可見,在濾除0.5%的(高頻)能量后,得到的濾波結果與原始圖像幾乎無差別。
4.2.2 巴特沃斯低通濾波器
在物理上可以實現的一種低通濾波器是巴特沃斯低通濾波器。一個階為n、截斷頻率為D0的巴特沃斯低通濾波器的轉移函數為
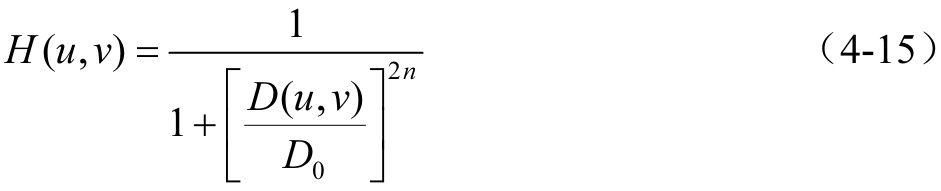
階為1的巴特沃斯低通濾波器轉移函數剖面圖如圖4-15所示,可見它在高低頻率間的過渡比較平滑,所以不僅可以在物理上實現,而且得到的輸出圖像也沒有明顯的振鈴效應。
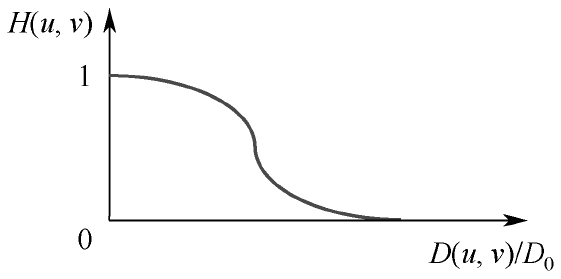
圖4-6 階為1的巴特沃斯低通濾波器轉移函數剖面圖
在一般情況下,常取使H(u,v)的值降到最大值的某個百分比的頻率為截斷頻率。在式(4-15)中,當D(u, v)=D0時,H(u, v) =0.5(降到最大值的50%)。另一個常用的截斷頻率是使H(u, v)的值降到最大值的 時的頻率。
時的頻率。
例4-4 利用頻域低通濾波消除虛假輪廓
當圖像由于量化不足而產生虛假輪廓時,常可用低通濾波進行平滑以改進圖像質量。圖4-7給出利用低通濾波消除虛假輪廓的示例。圖4-7(a)為一幅將256級灰度均勻量化為12級灰度的圖像,帽子和肩膀等處均有不同程度的虛假輪廓。圖4-7(b)和圖4-7(c)分別為用理想低通濾波器和用階數為1的巴特沃斯低通濾波器進行平滑處理的結果,其中兩個濾波器的截斷頻率所對應的半徑均為30。可見,理想低通濾波器的處理結果中存在較明顯的振鈴效應,而巴特沃斯濾波器的處理效果較好。

圖4-7 利用頻域低通濾波消除虛假輪廓的示例