2.1　線性規(guī)劃問題

一旦安裝了前面提到的JuMP包和優(yōu)化求解器，我們就能使用Julia很容易地解決LP和MILP問題了。例如，下面的這個LP問題。

max x1+2x2+5x3

其約束條件如下。

?x1+x2+3x3≤?5

x1+3x2 ?7x3≤10

0≤x1≤10

x2≥0

x3≥0

使用Julia和JuMP，我們可以將其寫成下面的代碼。

雖然上面的代碼非常容易理解，這里還是要解釋一下。我們首先聲明了一個優(yōu)化模型的占位符。

并在代碼中表明我們想使用GLPK優(yōu)化求解器，這里稱模型為m，之后聲明3個變量。

在這段代碼中，我們使用JuMP包中的宏@variable。在Julia中，宏為你做重復(fù)性的工作。這有些類似于函數(shù)，但與之有一些重要的不同之處。具體詳見官方文檔（參考資料[23]）。

我們用另一個宏@objective來設(shè)置對象。

并用宏@constraint增加兩個約束條件。

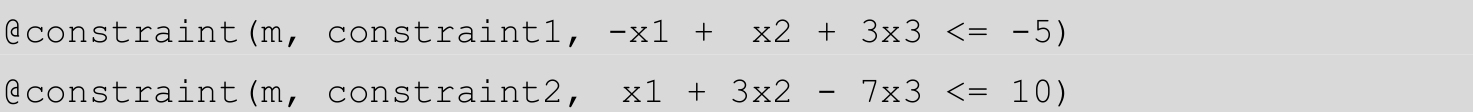
注意：constraint1和constraint2是約束條件的名稱，這些名稱將對獲取對應(yīng)的對偶變量值很有用。

現(xiàn)在對優(yōu)化問題已經(jīng)做好了準(zhǔn)備。現(xiàn)在就可以打印優(yōu)化模型，并檢查它是怎么寫的了，代碼如下所示。

解決優(yōu)化問題，如下所示。

解決了優(yōu)化問題后，我們可以使用JuMP.value()函數(shù)來獲取最優(yōu)條件下的變量值。

在上述代碼中，println()是在屏幕上將一些文本輸出為單獨的一行函數(shù)的。如果你不想這樣，可以使用print()函數(shù)。

要想獲取最優(yōu)對偶變量的值，請調(diào)用JuMP.shadow_price()，其對應(yīng)的約束名稱如下所示。

注意：這里還定義了JuMP.dual()函數(shù)。但是，JuMP.dual()函數(shù)結(jié)果的符號不會如你所愿，因為它遵循圓錐曲線二元性的原理。對線性優(yōu)化問題，JuMP.shadow_price()像大多數(shù)標(biāo)準(zhǔn)參考書那樣提供了對偶變量值。具體可參考JuMP文檔（參考資料[24]）和MathOptInterface文檔（參考資料[25]）中相關(guān)的討論。

在我的機器上，Gurobi的輸出如下所示。

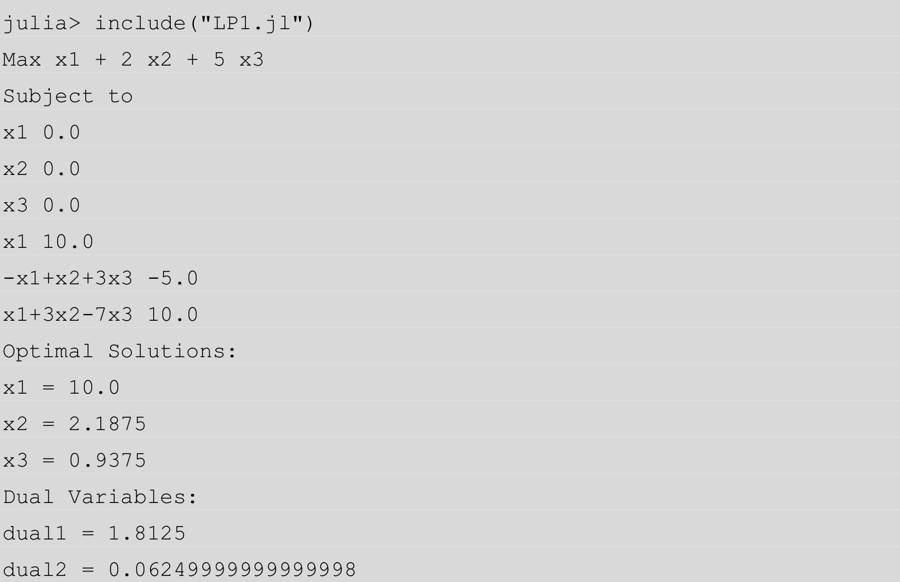
如果你想使用Gurobi優(yōu)化器而不是GLPK，請使用下面的輸入。

如果使用CPLEX，則用下面的輸入。

JuMP包還支持很多其他的優(yōu)化求解器，具體見JuMP手冊（參考資料[26]）。