国际在线财神捕鱼

書名：構建高質量軟件：持續集成與持續交付系統實踐
作者名：心藍
本章字數： 4840字
更新時間： 2021-10-09 14:32:58

1.5　測試驅動開發

測試驅動開發（Test Driven Development，TDD）是一種敏捷的軟件開發方法論，提倡在開發者開發足夠多的代碼之前優先編寫單元測試方法，然后重構開發者編寫的源代碼。一些剛入職場，或者對單元測試應用很少的開發者可能會有這樣的疑問：源代碼都沒有，單元測試要怎么寫？測試什么？請注意上述文字中的“開發足夠多的代碼之前”，這就意味著會有少量的源代碼開發工作優先于單元測試代碼的開發，比如開發一些功能模塊的骨架、方法的定義、方法模塊之間的依賴關系等基本代碼，否則就會真的什么也做不了。

關于測試驅動開發的概念，如果大家還想從理論上進一步深究，則請參考收錄在《計算機科學》刊物中的一篇論文“Using test-driven development to improve software development practices”，該論文對TDD進行了非常系統化、理論化的總結和描述，該論文地址為https://pdfs.semanticscholar.org/c7a8/205b4d8a8d3eee7b6d4f631c65d73a24cdb5.pdf。

1.5.1　紅–綠–重構

在TDD中有一個非常重要的紅–綠–重構三段式方法，可用于指導我們在實際開發中踐行TDD，本節就來詳細介紹該三段式方法所代表的含義。

“紅”指的是單元測試運行失敗的狀態，即在軟件中開發新特性、新功能，或者當現有的軟件出現缺陷對其進行重現時，我們首先需要開發新的單元測試代碼。由于此刻軟件的新功能并沒有具體的源代碼實現，因此單元測試的執行結果必然是失敗的，單元測試的運行狀態也必然是紅色狀態，如圖1-3所示。

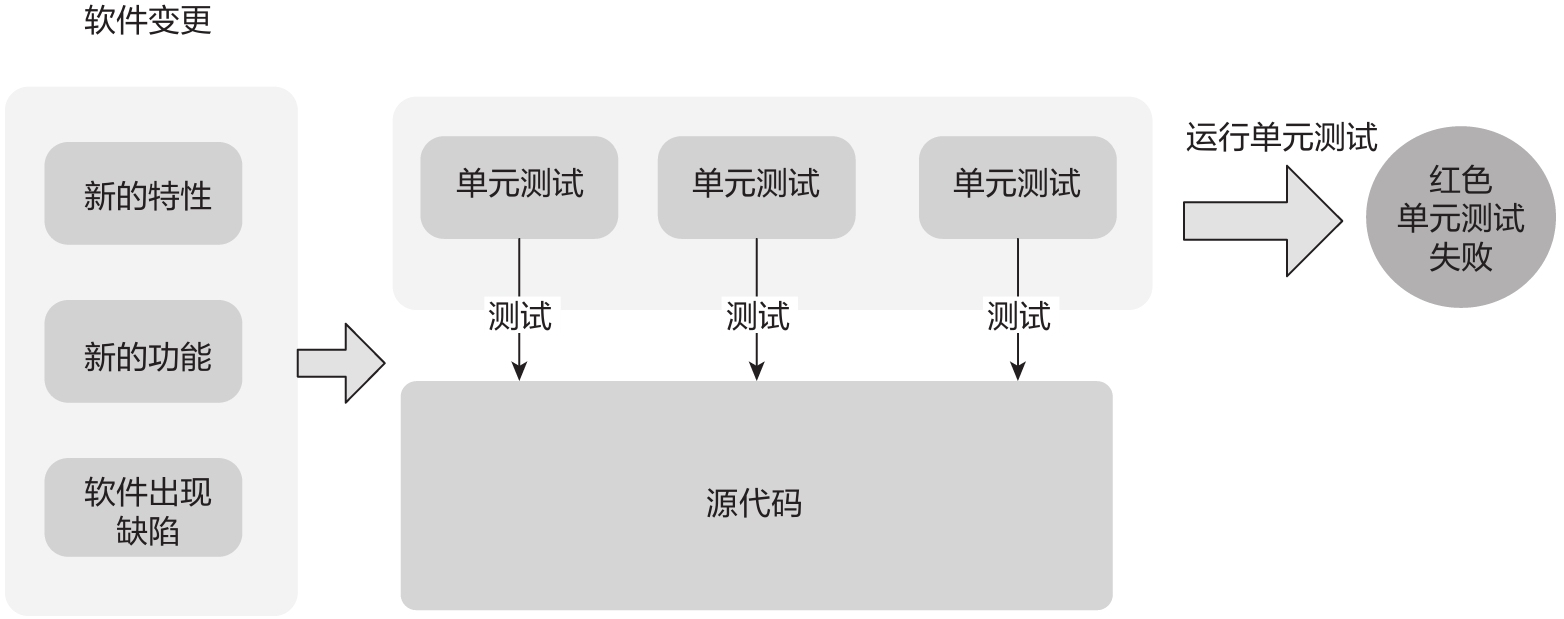
圖1-3　單元測試運行失敗的紅色階段

當單元測試運行失敗時，開發人員應該修改源代碼，使單元測試方法能夠順利通過運行。也就是說，單元測試執行失敗，將促使開發人員修復源代碼，使其正常運行，以達到讓所有單元測試都能成功運行的目的，這一階段即為綠色階段，如圖1-4所示。

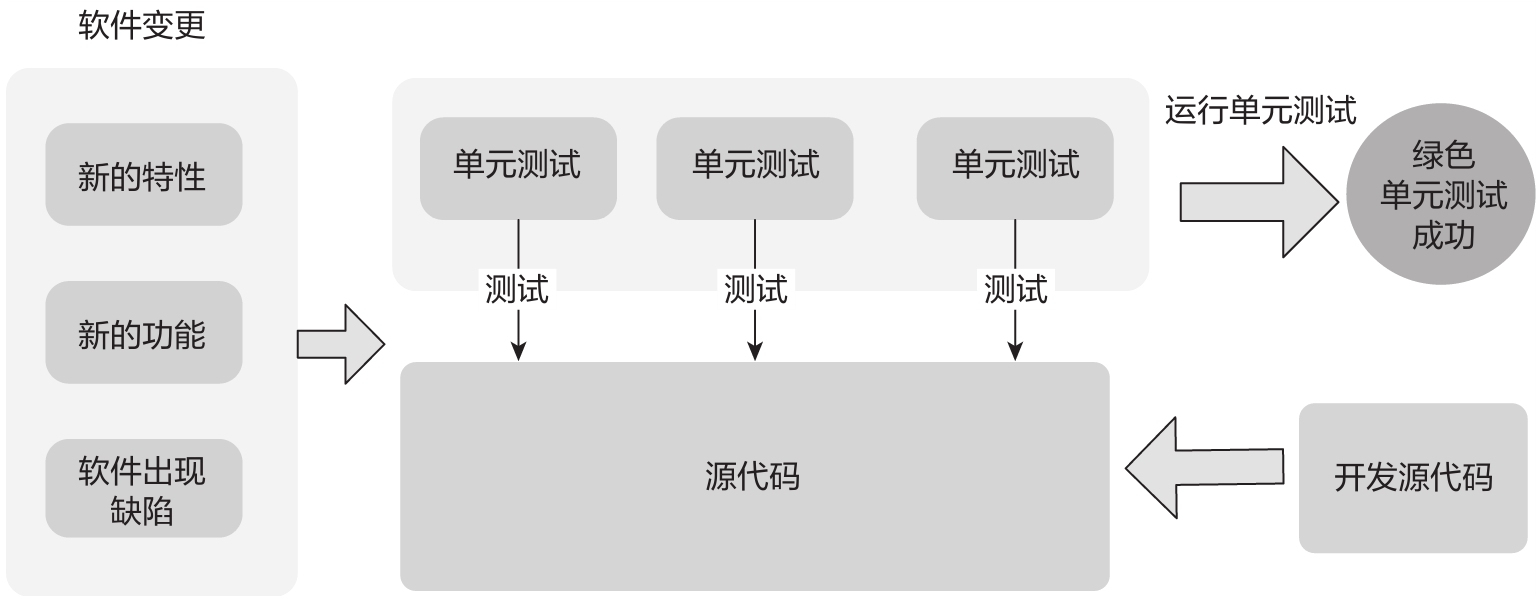
圖1-4　單元測試運行成功的綠色階段

開發人員通過對源代碼的開發，使所有的單元測試方法都能成功執行之后，整個開發過程并沒有完全完成。也許某些新增的源代碼還有一些可以進行優化和結構調整的地方，需要進一步拆解和抽象，因此接下來還有一個非常重要的階段，這就是重構，并且這三個階段需要反復執行多次（如圖1-5所示），才能最終確保開發者完成正確的程序開發。

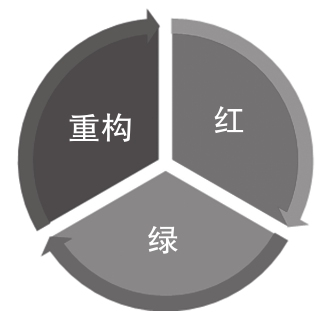
圖1-5　TDD紅–綠–重構三階段關系

對圖1-5各階段的說明如下。

1）紅色階段：代表軟件無法滿足某種功能，無論是新的功能需求還是已有的功能存在缺陷，都代表當前的軟件無法滿足某種功能。這種情況下，所有針對無法滿足特定功能的單元測試肯定是不能正常運行的。

2）綠色階段：單元測試無法成功執行，開發人員需要對源代碼進行相應的修改，無論是開發全新的代碼還是解決已有代碼的缺陷問題，當變更的源代碼使單元測試能夠正確執行時，就是所謂的綠色階段。但是僅僅使得現有的單元測試能夠順利執行還遠遠不夠，因為即使單元測試全部執行成功，也并不能代表所編寫的單元測試方法覆蓋了所有測試條件，下一輪的紅色階段或許還會將單元測試方法進一步拆分成粒度更小的單元測試方法，或者新增更多其他的單元測試方法。

3）重構階段：當所有的單元測試方法都能順利通過執行時，也并不意味著開發者所開發的代碼就是最終態了，代碼可能還需要進行結構的調整、邏輯的優化、容錯處理，以及各種依賴關系的抽象和重構等。在完成諸如此類的所有動作之后，還需要通過已有的單元測試和新增的單元測試驗證所做的操作是否正確。

1.5.2　TDD工作流程

如果你對TDD的紅–綠–重構三階段的理解還存在困難，覺得這些概念還是有些抽象，不用擔心，本節會將其進一步分解為若干個步驟，再結合開發人員日常熟悉的工作來進一步詳細說明。TDD的工作流程示意圖如圖1-6所示。

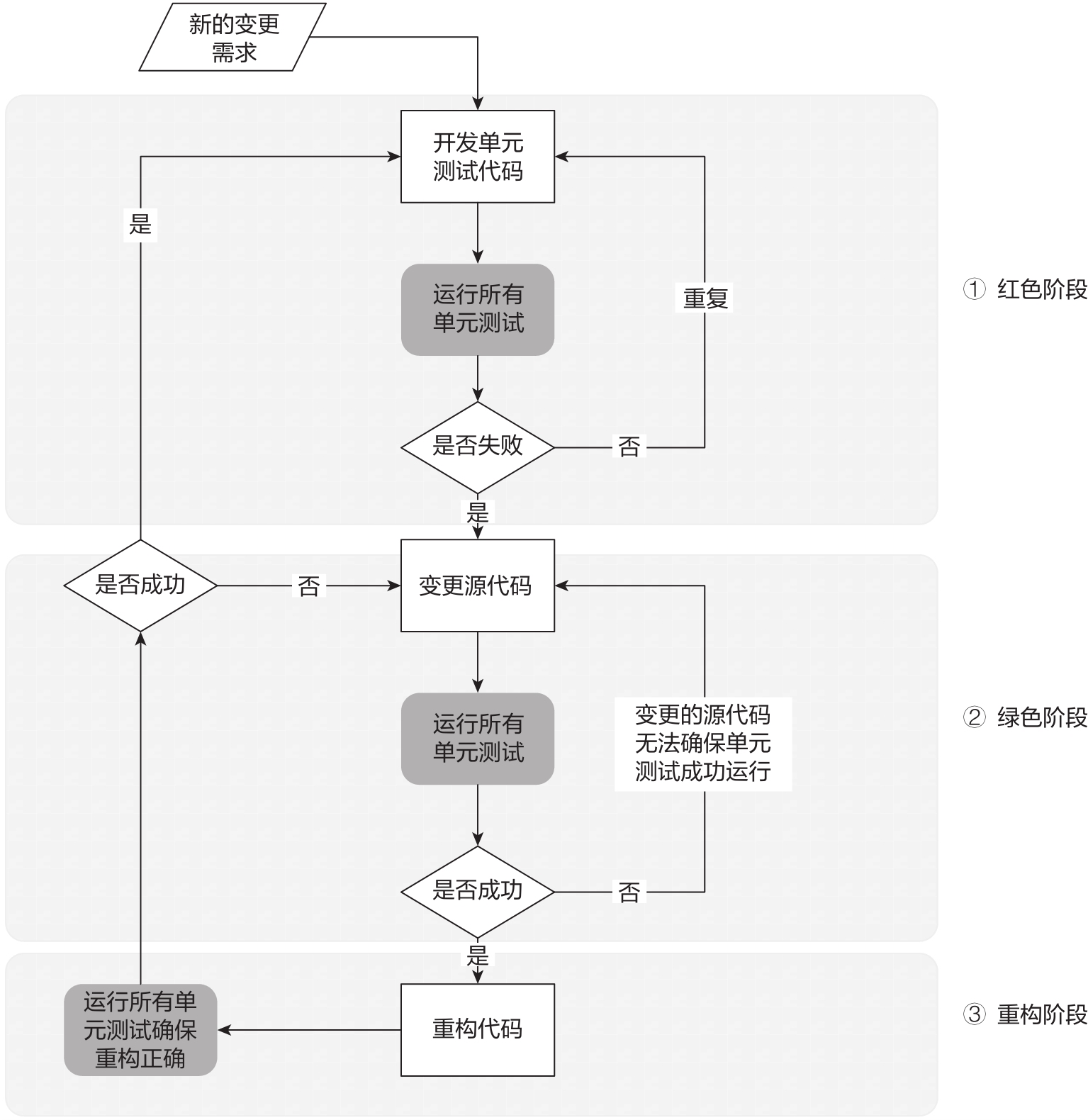
圖1-6　TDD工作流程步驟

圖1-6所示的TDD工作流程進一步細分了紅–綠–重構三個主要階段的工作流程步驟，其中，每個階段都需要執行單元測試，這也是我們反復強調的單元測試是TDD的基礎，也是持續集成和交付的基礎，因為它為軟件質量的保障提供了最重要的第一道關口。

1）編寫單元測試，用于驗證當前軟件是否滿足新的功能需求。

2）運行所有的單元測試，檢查是否存在失敗的單元測試代碼。

3）開發基本的功能代碼，使單元測試能夠成功執行。

4）運行單元測試，如果失敗則跳回步驟3。

5）重構代碼，并且再次運行單元測試代碼，以確保重構代碼的正確性，如果失敗則跳回步驟3。

6）重復整個流程，直到所有的測試條件都能順利通過驗證并充分覆蓋源代碼中的邏輯分支。

1.5.3　TDD實踐

了解了TDD的基本理論之后，下面就來講解如何將其應用在實際開發工作中，也就是我們通常所說的“落地”。在TDD方法論的實踐過程中，開發者需要反復不斷地思考，以確保程序代碼的正確性。本節將開發一個簡單的應用程序，并以此為例來實踐TDD的落地，示例程序將傳入數學表達式并輸出計算結果，比如輸入字符串“1+2”，計算結果為3.0，輸入字符串“2*3”，計算結果為6.0，等等。

簡單了解應用程序需要滿足的基本功能之后，下面我們就來著手開始相關的開發工作。首先，確定一個最基本的類NumericCalculator和基本的方法eval，具體實現如程序代碼1-5所示。

程序代碼1-5　NumericCalculator最初的框架代碼

//這里省略部分代碼。
public class NumericCalculator
{
    public double eval(String expression)
    {
        return 0.0D;
    }
}
//這里省略部分代碼。

“在開發足夠多”滿足eval方法的代碼之前，我們首先會開發若干個單元測試方法，對eval方法進行測試，最基本的運算表達式當然是“加減乘除”，測試方法如程序代碼1-6所示。

程序代碼1-6　NumericCalculatorTest單元測試

import org.junit.Before;
import org.junit.Test;

import static org.hamcrest.core.IsEqual.equalTo;
import static org.hamcrest.MatcherAssert.assertThat;

public class NumericCalculatorTest
{
    private NumericCalculator calculator;

    @Before
    public void setup()
    {
        this.calculator = new NumericCalculator();
    }

    @Test
    public void textEvalAddExpression()
    {
        final String expression = "1+2";
        assertThat(calculator.eval(expression), equalTo(3.0D));
    }

    @Test
    public void textEvalSubtractExpression()
    {
        final String expression = "3-1";
        assertThat(calculator.eval(expression), equalTo(2.0D));
    }

    @Test
    public void textEvalMultiplyExpression()
    {
        final String expression = "3*2";
        assertThat(calculator.eval(expression), equalTo(6.0D));
    }

    @Test
    public void textEvalDivideExpression()
    {
        final String expression = "3/2";
        assertThat(calculator.eval(expression), equalTo(1.5D));
    }
}

根據最基本的數學運算方法，我們分別開發了“加減乘除”四個最基本的單元測試，并且對其進行了斷言操作。運行上面的單元測試，我們會發現所有的單元測試方法都無法通過測試（如圖1-7所示），也就是說出現了失敗的測試用例方法，這一階段就是上文所描述的“紅色”階段。

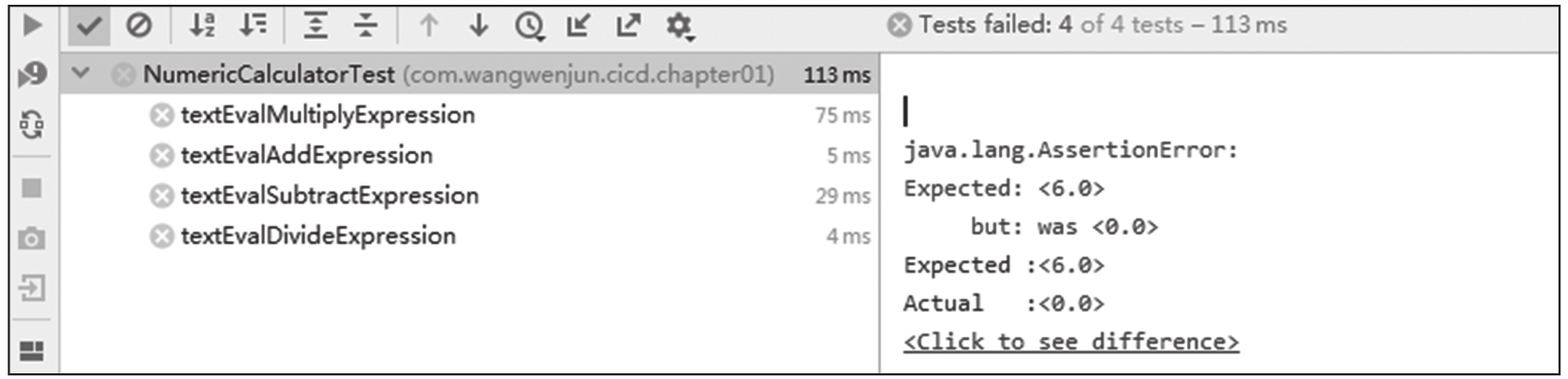
圖1-7　單元測試執行失敗

根據1.5.1節和1.5.2節中關于TDD三大階段及執行流程步驟的描述，當單元測試運行失敗時，我們需要更新相關的源代碼，使單元測試方法能夠正常運行，因此我們增加了計算邏輯的eval方法，具體實現如程序代碼1-7所示。

程序代碼1-7　eval方法實現基本的數學運算

//這里省略部分代碼。
public double eval(String expression)
{
    final String operation;
    final String[] data;
    if (expression.contains("+"))
    {
        operation = "+";
        data = expression.split("\\+");
    } else if (expression.contains("-"))
    {
        operation = "-";
        data = expression.split("-");
    } else if (expression.contains("*"))
    {
        operation = "*";
        data = expression.split("\\*");
    } else if (expression.contains("/"))
    {
        operation = "/";
        data = expression.split("/");
    } else
        throw new IllegalArgumentException("Unrecognized operator.");

    switch (operation)
    {
        case "+":
            return Double.parseDouble(data[0]) + Double.parseDouble(data[1]);
        case "-":
            return Double.parseDouble(data[0]) - Double.parseDouble(data[1]);
        case "*":
            return Double.parseDouble(data[0]) * Double.parseDouble(data[1]);
        case "/":
            return Double.parseDouble(data[0]) / Double.parseDouble(data[1]);
        default:
            throw new UnsupportedOperationException();
    }
}
//這里省略部分代碼。

當我們完成了對eval方法的代碼開發之后，再次運行所有的單元測試，會發現每一個測試用例方法都能正確運行（如圖1-8所示），這一階段就是上文所描述的“綠色”階段。

圖1-8　單元測試執行成功

就像上文所提到的，雖然功能源代碼能夠保證最基本的單元測試方法都能順利通過并正常運行，但是目前源代碼的設計仍然非常粗糙，比如eval方法職責太重，除了要解析表達式字符串之外，還承載了數學運算。另外，該方法中存在大量的重復性代碼。因此我們需要對其進行重構，重構的最基本思想是將參與運算的數據和運算符號抽象出來，并將表達式的解析從eval方法中抽取出來。重構后的eval方法如程序代碼1-8所示。

程序代碼1-8　重構后的eval方法

//這里省略部分代碼。
public double eval(String expression)
{
    final Expression expr = Expression.of(expression);
    switch (expr.getOperator())
    {
        case ADD:
            return expr.getLeft() + expr.getRight();
        case SUBTRACT:
            return expr.getLeft() - expr.getRight();
        case MULTIPLY:
            return expr.getLeft() * expr.getRight();
        case DIVIDE:
            return expr.getLeft() / expr.getRight();
        default:
            throw new UnsupportedOperationException();
    }
}
//這里省略部分代碼。

重構后的eval方法看起來簡潔、清晰了很多，屏蔽了表達式expression的解析過程，減少了代碼的重復，但是也由此引入了新的代碼結構，即新增了對Expression類的依賴，Expression類的實現如程序代碼1-9所示。

程序代碼1-9　Expression類的實現

package com.wangwenjun.cicd.chapter01;

public class Expression
{
    enum Operator
    {
        ADD("+"),
        SUBTRACT("-"),
        MULTIPLY("*"),
        DIVIDE("/");
        private final String opt;

        Operator(String opt)
        {
            this.opt = opt;
        }

        @Override
        public String toString()
        {
            return opt;
        }
    }

    private final Operator operator;
    private final double left;
    private final double right;

    public static Expression of(Operator operator, double left, double right)
    {
        return new Expression(operator, left, right);
    }

    public static Expression of(String expression)
    {
        if (expression.contains("+"))
        {
            String[] data = expression.split("\\+");
            return of(Operator.ADD, Double.parseDouble(data[0]), Double.parseDouble
                (data[1]));
        } else if (expression.contains("-"))
        {
            String[] data = expression.split("-");
            return of(Operator.SUBTRACT, Double.parseDouble(data[0]), Double.parseDouble
                 (data[1]));
        } else if (expression.contains("*"))
        {
            String[] data = expression.split("\\*");
            return of(Operator.MULTIPLY, Double.parseDouble(data[0]), Double.parseDouble
                 (data[1]));
        } else if (expression.contains("/"))
        {
            String[] data = expression.split("/");
            return of(Operator.DIVIDE, Double.parseDouble(data[0]), Double.
                 parseDouble(data[1]));
        } else
        {
            throw new IllegalArgumentException("Unrecognized operator.");
        }
    }

    public Expression(Operator operator, double left, double right)
    {
        this.operator = operator;
        this.left = left;
        this.right = right;
    }

    public Operator getOperator()
    {
        return operator;
    }

    public double getLeft()
    {
        return left;
    }

    public double getRight()
    {
        return right;
    }
}

至此，重構階段的任務已全部完成。需要注意的是，不要忘記在代碼重構完成之后繼續執行所有的單元測試代碼，以確保重構的代碼是正確的。

實際上，TDD的實踐過程就是一個不斷思考和迭代的過程，其會推動開發者不斷思考怎樣做才能使項目程序足夠正確和穩健，比如，針對目前的eval方法，我們還可以思考如下的問題。

如果eval方法中傳入的表達式expression為空或null怎么辦？
如果表達式中不包含任何運算符號怎么辦？
如果表達式中包含除了運算符之外的非數字內容怎么辦？
如果表達式不完整（比如“1+”）怎么辦？
如果進行除法運算時，除數為0怎么辦？

答案是增加新的測試代碼，繼續回到“紅色”階段，程序代碼1-10所示的是新增的單元測試代碼，其中的代碼注釋詳細描述了每個單元測試的測試意圖。

程序代碼1-10　新增的單元測試方法

//當表達式字符串為空時，期望拋出IllegalArgumentException異常。
@Test(expected = IllegalArgumentException.class)
public void testExpressionStringBlack()
{
    calculator.eval("");
}
//當表達式字符串為null時，期望拋出IllegalArgumentException異常。
@Test(expected = IllegalArgumentException.class)
public void testExpressionStringNull()
{
    calculator.eval(null);
}
//當表達式包含不支持的運算符時，期望拋出IllegalArgumentException異常。
@Test(expected = IllegalArgumentException.class)
public void testExpressionNoOperator()
{
    calculator.eval("1?2");
}

//當表達式包含非數字數值時，期望拋出IllegalArgumentException異常。
@Test(expected = IllegalArgumentException.class)
public void testExpressionNotNumeric()
{
    calculator.eval("x+y");
}

//當表達式非法時，期望拋出IllegalArgumentException異常。
@Test(expected = IllegalArgumentException.class)
public void testExpressionInvalid()
{
    calculator.eval("1+");
}

//當表達式除數為0時，期望拋出IllegalArgumentException異常。
@Test(expected = IllegalArgumentException.class)
public void testExpressionDivisorIsZero()
{
    calculator.eval("1/0");
}

繼續執行所有的單元測試方法，我們會看到運行結果中出現了運行失敗的單元測試用例方法，如圖1-9所示。

圖1-9　部分單元測試方法執行失敗

此刻再次進入“綠色階段”，我們需要進一步修改代碼，使單元測試方法能夠正常運行。由于源代碼越來越多，需要考慮的細節也越來越多，因此這次修改代碼所要涉及的地方會更多一些。為了方便起見，筆者將所有的代碼更改都匯合在一起進行展示，如程序代碼1-11所示（為了節約篇幅，未變動的源代碼會省略，具體請參考隨書代碼）。

程序代碼1-11　修改后的計算器程序

//修改NumericCalculator類的eval方法，增加了對輸入表達式expression是否為空的判斷。
public double eval(String expression)
{
    if (null == expression || expression.isEmpty())
        throw new IllegalArgumentException("the expression can't be null or black.");
    final Expression expr = Expression.of(expression);
//這里省略部分代碼。

//修改枚舉Operator類，增加了類型映射方法。
//這里省略部分代碼。
private static Map<String, Operator> typeMapping = new HashMap<>();
static
{
    typeMapping.put(ADD.opt, ADD);
    typeMapping.put(SUBTRACT.opt, SUBTRACT);
    typeMapping.put(MULTIPLY.opt, MULTIPLY);
    typeMapping.put(DIVIDE.opt, DIVIDE);
}
public static Operator getOperator(String opt)
{
    return typeMapping.get(opt);
}

//這里省略部分代碼。
//重寫Expression的of方法，使用正則表達式對字符串進行split操作，使代碼更加簡潔。
private final static String regexp = "^(\\d+)([\\+|\\-|\\*|\\/])(\\d+)$";
private final static Pattern pattern = Pattern.compile(regexp);
public static Expression of(String expression)
{
    final Matcher matcher = pattern.matcher(expression);
    if (!matcher.matches())
        throw new IllegalArgumentException("Illegal expression.");
    final Expression exp = of(Operator.getOperator(matcher.group(2)),
            Double.parseDouble(matcher.group(1)),
            Double.parseDouble(matcher.group(3)));
    if (exp.getOperator() == Operator.DIVIDE && exp.getRight() == 0)
        throw new IllegalArgumentException("The divisor cannot be zero. ");
    return exp;
//這里省略部分代碼。

至此，源代碼已全部修改完畢。現在所有的單元測試考驗都可以正常通過了（限于篇幅，此處省略單元測試的執行過程，大家可以自行測試運行），接下來無須再進行進一步的重構工作，可以提交當前數值計算器的初級版本了。雖然該版本看起來還是比較脆弱，不支持多個數值的計算，不支持“加減乘除”優先級，不支持大括號、小括號、花括號，不支持高階的數學運算，但這些對我們來說都是新的需求，只有當需要的時候才會進行進一步的完善和開發，我們可以將其納入任務列表（Sprint Backlog）中，通過項目的不斷迭代，實現更復雜、更強大的表達式計算操作。

那么，單元測試到底有沒有覆蓋到所有的測試條件和可能性呢？除了開發人員進行人工分析之外，更嚴謹的做法是再借助測試覆蓋率工具（如圖1-10所示），進一步確認是否有必要補充新的單元測試方法。

圖1-10　單元測試覆蓋率報告

從圖1-10所示的覆蓋率報告來看，除了枚舉類Operator的toString()方法沒有進行測試之外，單元測試覆蓋率幾乎達到100%，這也從側面印證了應用TDD這一敏捷方法論可以很好地完成基本數學表達式的解析和運算功能。

擴展閱讀：如果想要實現更復雜的數學表達式計算，可以借助數據結構Stack來實現，“1+2”這樣的表達式是我們比較習慣的“中綴表達式”，可以將其轉換為“右綴表達式”（比如“12+”，代表1和2相加），分別將數值和運算符壓入兩個棧中，然后用彈棧的方式進行計算，即可實現更復雜的數學表達式計算（比如1+2+3×4–2+100/5等）。隨著對()、[]和{}符號，以及其他數學運算（比如乘方、三角函數等）的引入，程序會變得越來越復雜，這里推薦一個非常好用的第三方類庫exp4j，通過下面的方式將其引入項目工程中即可。

<dependency>
    <groupId>net.objecthunter</groupId>
    <artifactId>exp4j</artifactId>
    <version>0.4.8</version>
</dependency>

我們可以寫一個簡單的單元測試方法來驗證exp4j的功能，代碼如下。

@Test
public void testExp4j()
{
    net.objecthunter.exp4j.Expression expression =
        new ExpressionBuilder("(1+2)*10-5/3+40").build();
    double result = expression.evaluate();
    assertThat(result, equalTo(68.33333333333333D));
}

exp4j不僅支持很多種類的數學計算，而且支持變量名定義、異步運算等，如果對該類庫感興趣，則可以通過如下官網地址獲取更多幫助。

exp4j庫的官網地址為https://www.objecthunter.net/exp4j/。

官术网_书友最值得收藏!

構建高質量軟件：持續集成與持續交付系統實踐

1.5 測試驅動開發

1.5.1 紅–綠–重構

1.5.2 TDD工作流程

1.5.3 TDD實踐

1.5　測試驅動開發

1.5.1　紅–綠–重構

1.5.2　TDD工作流程

1.5.3　TDD實踐