1.4　開始學習神經網絡

現在，我們知道神經網絡是深度學習的核心，是現代計算機視覺的強大工具。但它們到底是什么呢？它們是如何工作的？下面，我們將不僅討論它們效率背后的理論解釋，而且還將直接將這些知識用于一個識別任務的簡單網絡的實現和應用。

1.4.1　建立神經網絡

人工神經網絡（Artificial Neural Network，ANN）或神經網絡（Neural Network，NN）是強大的機器學習工具，擅長處理信息、識別常見模式或檢測新模式以及模擬復雜的過程。這些優勢得益于它們的結構，我們接下來將揭示這一點。

模擬神經元

眾所周知，神經元是思想和反應的基本單元。但是它們實際上是如何工作的，以及應如何模擬它們，對研究人員來說并不是顯而易見的。

生物啟發

的確，人工神經網絡靈感多少來自動物大腦的工作模式。大腦是一個由神經元組成的復雜網絡，每個神經元相互傳遞信息，并將感官輸入（如電信號和化學信號）轉化為思想和行動。每個神經元的電輸入來自它的樹突，樹突是一種細胞纖維，它將來自突觸（與前一神經元相連的節點）的電信號傳遞到神經元胞體（神經元的主體）。如果累積的電刺激超過特定閾值，細胞就會被激活，電脈沖通過細胞的軸突（神經元的輸出電纜，連接其他神經元的突觸）進一步傳播到下一個神經元。因此，每個神經元都可以被看作是一個非常簡單的信號處理單元，一旦堆疊在一起，就可以實現我們現在的思想。

數學模型

受其生物表示的啟發（見圖1-11），人工神經元有幾個輸入（每個數據都有一個序號），將輸入累加在一起，最后使用一個激活函數（activation function）來獲得輸出信號，輸出可以傳遞給網絡中的下一個神經元（這可以視為一個有向圖）。

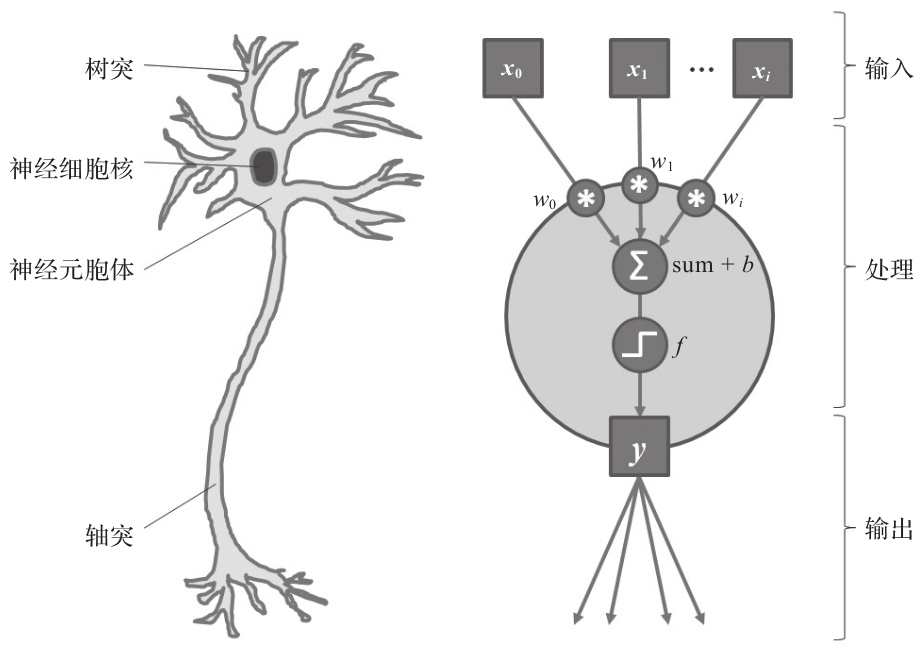
圖1-11　簡化的生物神經元（左）和人工神經元（右）

通常以加權方式計算輸入求和。每個輸入都是按照特定于輸入的權重放大或縮小的。這些權重是在網絡訓練階段進行優化調整的參數，以使神經元對適當的特征做出反應。通常，另一個參數（神經元的偏置）也被訓練并用于這個求和過程。它的值只是作為偏移量加到加權和中。

我們來快速地用數學方法表示這個過程。假設我們有一個神經元，它有兩個輸入值，x₀和x₁。這些值的加權系數分別為w₀和w₁，可選的偏置為b。為了簡化，將輸入值表示為水平向量x，將權重表示為垂直向量w：

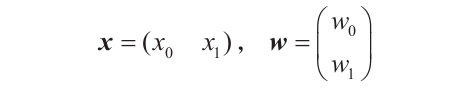
因此，整個運算可以簡單地表示為：

z=x·w+b

這一步很簡單，不是嗎？兩個向量之間的點積負責加權求和：

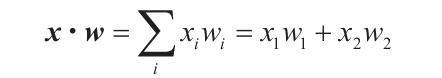
現在輸入已經被縮放和相加成結果z了，我們需要對它應用激活函數來得到神經元的輸出。回到與生物神經元的類比，它的激活函數將是一個二元函數，當y超過閾值t時，返回一個電脈沖（即1），否則返回0（通常情況下t=0）。如果將其用數學公式表示，那么激活函數y=f（z）可以表示為：

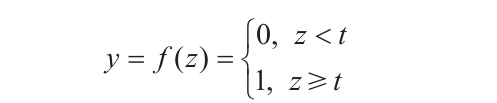
階躍函數是原始感知機的關鍵組成部分，但研究人員早期就已經引入了更高級的激活函數，它們具有更好的特性，如非線性（用于對更復雜的行為建模）和連續可微性（這對于訓練過程很重要，將在后面解釋）。最常見的激活函數如下：

·sigmoid函數：

·雙曲正切函數：

·修正線性單元：

上述常見激活函數的示意圖如圖1-12所示。

圖1-12　常見激活函數示意圖

對于所有的神經網絡，基本都是以上的邏輯！這樣我們就模擬了一個簡單的人工神經元。它能夠接收一個信號，處理它，并輸出一個值，這個值可以被前向傳遞（前向傳遞是機器學習中常用的術語）給其他神經元，從而構建一個網絡。

將多個沒有非線性激活函數的神經元鏈接起來，本質上仍相當于一個神經元。例如，如果有一個參數為w_A和b_A的線性神經元，其后鏈接一個參數為w_B和b_B的線性神經元，那么

y_B=w_B·y_A+b_B=w_B·（w_A·x+b_A）+b_B=w·x+b

其中，w=w_A·w_B，b=b_A+b_B。因此，如果想要創建復雜的模型，非線性激活函數是必要的。

實現

以上模型可以簡便地基于Python實現（使用numpy進行向量和矩陣運算）：

如上段代碼所示，這是對我們之前定義的數學模型的直接改編。使用這個人工神經元也很簡單。我們來實例化一個感知機（使用階躍函數為激活方法的神經元），并通過它前向傳遞一個隨機輸入：

在進入下一節開始擴大它們的規模之前，建議先花點時間用不同的輸入和神經元參數進行一些實驗。

將神經元分層組合在一起

通常，神經網絡被組織成多層，也就是說，每層的神經元通常接收相同的輸入并應用相同的操作（例如，盡管每個神經元首先用自己特定的權重來對輸入求和，但是它們應用相同的激活函數）。

數學模型

在網絡中，信息從輸入層流向輸出層，中間有一個或多個隱藏層。在圖1-13中，3個神經元A、B、C分別屬于輸入層，神經元H屬于輸出層或激活層，神經元D、E、F、G屬于隱藏層。第一層輸入x的維度為2，第二層（隱藏層）將前一層的三個激活值作為輸入，以此類推。這類每個神經元均連接到前一層的所有值的網絡，被稱為全連接或稠密網絡。

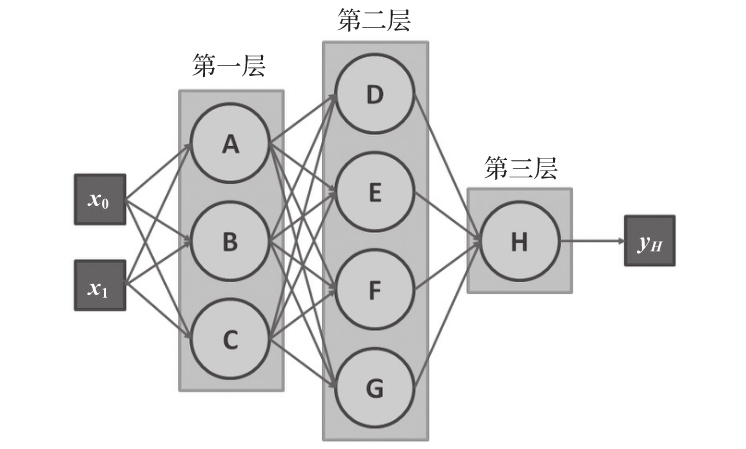
圖1-13　有兩個輸入值和一個最終輸出的三層神經網絡

同樣，通過用向量和矩陣表示這些元素來簡化計算表達。以下操作由第一層完成：

z_A=x·w_A+b_A

z_B=x·w_B+b_B

z_C=x·w_C+b_C

這可以表示為：

z=x·W+b

為了得到前面的方程，必須定義如下的變量：

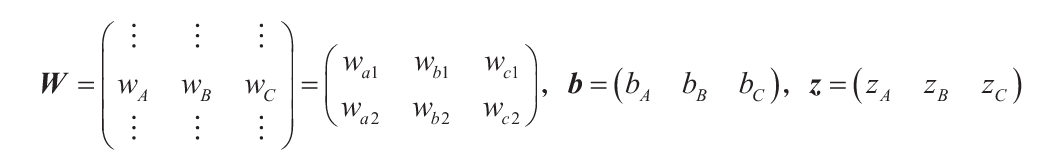
因此，第一層的激活函數可以寫成一個向量y=f（z）=（f（z_A） f（z_B） f（z_C）），它可以作為輸入向量直接傳遞到下一層，以此類推，直到最后一層。

實現

與單個神經元一樣，這個模型也可以用Python實現。事實上，我們甚至不需要對Neuron類做太多的編輯：

我們只需要改變一些變量的維度來反映一個層內神經元的多樣性。有了這個實現，每層甚至可以一次處理多個輸入！傳遞一個列向量x（向量形狀是1×s，其中s是x中數值的個數）或一組列向量（向量形狀為n×s，其中n是樣本的數量）不會改變任何關于矩陣的計算，并且網絡的層都將正確輸出疊加的結果（假設每一行與b相加）：

一組輸入數據通常稱為一批（batch）。

有了這個實現，只需將全連接的層連接在一起就可以構建簡單的神經網絡。

將網絡應用于分類

我們已經知道了如何定義層，但還沒有將其初始化并連接到計算機視覺網絡中。為了演示如何做到這一點，我們將處理一個著名的識別任務。

設置任務

對手寫數字的圖像進行分類（即識別圖像中是否包含0或1等）是計算機視覺中的一個歷史性問題。修正的美國國家標準與技術研究院（Modified National Institute of Standards and Technology，MNIST）數據集（http://yann.lecun.com/exdb/mnist/）包含70 000張灰度數字圖像（像素為28×28），多年來一直作為參考，方便研究人員通過這個識別任務測試他們的算法（Yann LeCun和Corinna Cortes享有這個數據集的所有版權，數據集如圖1-14所示）。

圖1-14　MNIST數據集中每個數字的10個樣本

對于數字分類，我們需要的是一個將這些圖像中的一個作為輸入并返回一個輸出向量，該向量表示網絡認為的這些圖像與每個類對應的概率。輸入向量有28×28=784個值，而輸出有10個值（對于從0到9的10個不同數字）。在輸入和輸出之間，由我們來定義隱藏層的數量和它們的大小。要預測圖像的類別，只需通過網絡前向傳遞圖像向量，收集輸出，然后返回置信度得分最高的類別即可。

這些置信度得分通常被轉化為概率值，以簡化后續的計算或解釋。例如，假設一個分類網絡給類“狗”賦值為9，給另一個類“貓”賦值為1。這就是說，根據這個網絡，圖像顯示的是狗的概率為9/10，顯示的是貓的概率為1/10。

在實現解決方案之前，先通過加載MNIST數據來完成用于訓練和測試算法的數據準備。為了簡單起見，我們將使用由Marc Garcia開發的Python mnist模塊（https://github.com/datapythonista/mnist）（根據BSD 3-Clause的新/修訂許可，已經安裝在本章的源目錄中）：

關于數據集預處理和可視化的更詳盡操作可以在本章的源代碼中找到。

實現網絡

對于神經網絡本身，我們必須把層組合在一起，并添加一些算法在整個網絡上進行前向傳遞，然后根據輸出向量來預測分類。在實現各層之后，下面的代碼就不言自明了：

我們剛剛實現了一個前饋神經網絡，可以用來分類！是時候把它應用到我們的問題上了：

我們的準確率只有12.06%。這可能看起來令人失望，因為它的準確性僅略好于隨機猜測。但是這是有意義的——因為此時的網絡是由隨機參數定義的。我們需要根據用例來訓練它，這就是下一節中需要處理的任務。

1.4.2　訓練神經網絡

神經網絡是一種特殊的算法，因為它們需要訓練，也就是說，它們需要通過從可用的數據中學習來針對特定的任務進行參數優化。一旦網絡被優化至在訓練數據集上表現良好，它們就可以在新的、類似的數據上使用，從而提供令人滿意的結果（如果訓練正確的話）。

在解決MNIST任務之前，我們將介紹一些理論背景，涵蓋不同的學習策略，并介紹實際中是如何進行訓練的。然后，將直接把這些概念應用到示例中，以便我們的簡單網絡最終學會如何解決識別任務！

學習策略

當涉及神經網絡學習時，根據任務和訓練數據的可用性，主要有三種學習范式。

有監督學習

有監督學習（supervised learning）可能是最常見的，當然也是最容易掌握的學習范式。當我們想要教會神經網絡兩種模式之間的映射關系（例如，將圖像映射到它們的類標簽或它們的語義掩膜）時，適合使用有監督學習。它需要訪問一個包含圖像及其真值標簽（例如每張圖像的類信息或語義掩膜）的訓練數據集。

這樣一來，訓練就很簡單了：

·將圖像提供給網絡，并收集其結果（即預測標簽）。

·評估網絡的損失，即將預測結果與真值標簽進行比較時的錯誤程度。

·相應地調整網絡參數以減少損失。

·重復以上操作直至網絡收斂，也就是說，直到它在這批訓練數據上不能再進一步改進為止。

這種學習策略確實可以形容為“有監督的”，因為有一個實體（即我們）通過對每個預測結果提供反饋（根據真值標簽計算出的損失）來監督網絡的訓練情況，以便該算法可以通過重復訓練（觀察某次訓練是正確的或錯誤的，然后再試一次）來學習。

無監督學習

然而，當沒有任何真值信息可用時，如何訓練網絡？答案是采用無監督學習（unsupervised learning）。它的思想是創建一個函數，僅根據網絡的輸入和相應的輸出來計算網絡的損失。

這種策略非常適用于聚類（將具有相似屬性的圖像分組在一起）或壓縮（減少內容大小，同時保留一些屬性）等應用程序。對于聚類，損失函數可以衡量來自某一類相似圖像與其他類圖像的比較情況。對于壓縮，損失函數可以衡量壓縮后的數據與原始數據相比，重要屬性的保留程度。

無監督學習需要一些關于用例的專業知識，才能提出有意義的損失函數。

強化學習

強化學習（reinforcement learning）是一種交互式策略。智能體在環境中導航（例如，機器人在房間中移動或電子游戲角色通過關卡）。智能體有一個預定義的、可執行的動作列表（走、轉、跳等），并且在每個動作之后，它會進入一個新的狀態。有些狀態可以帶來“獎勵”，這些獎勵可以是即時的，也可以是延遲的，可以是正面的，也可以是負面的（例如，游戲角色獲得額外物品時的正面獎勵，游戲角色被敵人擊中時的負面獎勵）。

在每個時刻，神經網絡只提供來自環境的觀察（例如，機器人的視覺輸入或視頻游戲屏幕）和獎勵反饋（胡蘿卜和大棒）。由此，它必須了解什么能帶來更高的獎勵并據此為智能體制定最佳的短期或長期策略。換句話說，它必須評估出能使其最終獎勵最大化的一系列行為。

強化學習是一個強大的學習范式，但是很少用于計算機視覺用例。雖然我們鼓勵機器學習愛好者學習更多的知識，但在這里我們不會再做進一步介紹。

訓練時間

不管學習策略是什么，大致的訓練步驟都是一樣的。給定一些訓練數據，網絡進行預測并接收一些反饋（如損失函數的結果），然后用這些反饋更新網絡的參數。然后重復這些步驟，直到無法進一步優化網絡為止。本節將詳細介紹并實現這個過程，從損失計算到優化權重。

評估損失

損失函數的目標是評估網絡在其當前權重下的性能。更正式地說，這個函數將預測效果表示為網絡參數（比如它的權重和偏置）的函數。損失越小，針對該任務的參數就越好。

因為損失函數代表了網絡的目標（例如，返回正確的標簽，壓縮圖像同時保留內容，等等），所以有多少任務就有多少不同的函數。盡管如此，有些損失函數比其他函數更常用一些，比如平方和函數，也稱為L2損失函數（基于L2范數），它在有監督學習中無處不在。這個函數簡單地計算輸出向量y的每個元素（網絡估計的每個類的概率）和真值y^true向量（除了正確的類之外，該目標向量中對應的其余每個類都是空值）的每個元素之間的差的平方：

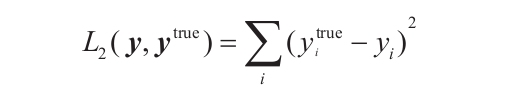
還有許多其他性質不同的損失函數，如計算矢量之間絕對差的L1損失，如二進制交叉熵（Binary Cross-Entropy，BCE）損失，它把預測概率轉換為對數，然后與預期的值進行比較：

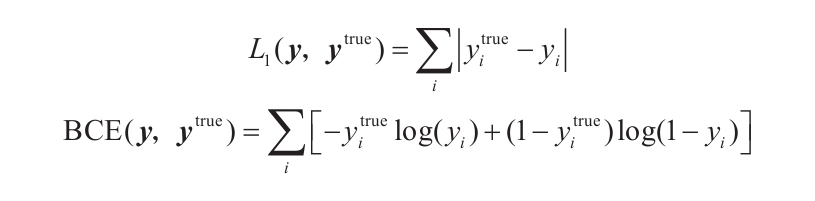
對數運算將概率從[0，1]轉換為[-∞，0]，因此將結果乘以-1，神經網絡在學習如何正確預測時損失值的區間就可以變換為[0，+∞]。請注意，交叉熵函數也可以應用于多分類的問題（不僅僅局限于兩類）。

人們通常會將損失值除以向量中元素的數量，也就是說，計算平均值而不是損失總和。均方誤差（Mean-Square Error，MSE）是L2損失的平均值，平均絕對誤差（Mean-Absolute Error，MAE）是L1損失的平均值。

現在，我們將以L2損失為例，并在后面的理論解釋和MNIST分類器訓練中用到它。

反向傳播損失

如何更新網絡參數，才能使其損失最小？對于每個參數，我們需要知道的是改變它的值會如何影響損失。如果知道哪些變化會使損失減少，那么只需重復應用這些變化，直到損失達到最小即可。這正是損失函數梯度的原理，也是梯度下降的過程。

在每次訓練迭代中，計算損失函數對網絡各參數的導數。這些導數表示需要對參數進行哪些小的更改（由于梯度表示函數上升的方向，而我們希望最小化它，因此這里有一個為-1的系數）。它可以看作是沿著損失函數關于每個參數的斜率逐步下降，因此這個迭代過程被稱為梯度下降（見圖1-15）。

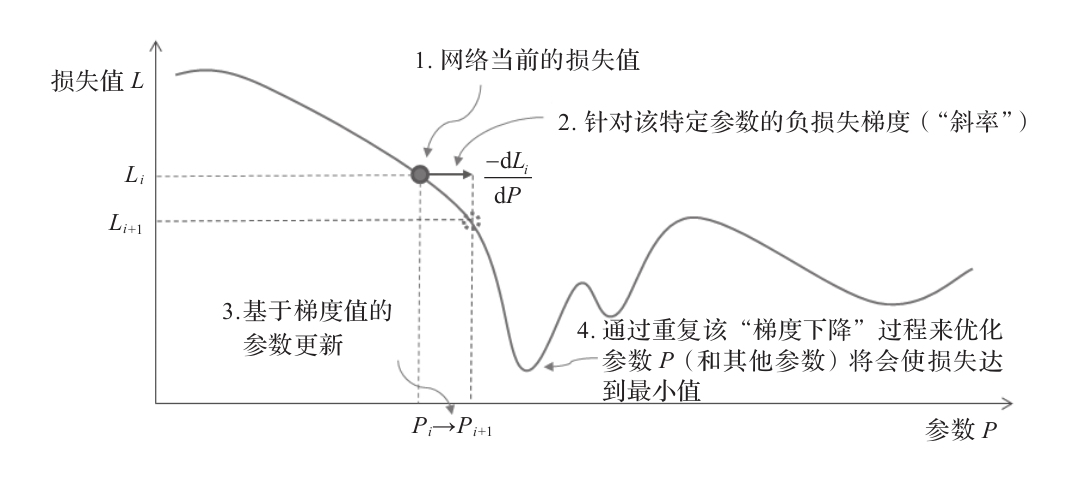
圖1-15　優化神經網絡參數P的梯度下降過程示意圖

現在的問題是，如何計算所有這些導數（即斜率值，以作為每個參數的函數）？這時鏈式法則就派上用場了。并不需要太深入的微積分知識，鏈式法則可以告訴我們，關于k層參數的導數可以簡單地用該層的輸入和輸出值（x_k，y_k），以及k+1層的導數來計算。更正式地說，對于該層的權值W_k，有以下公式：

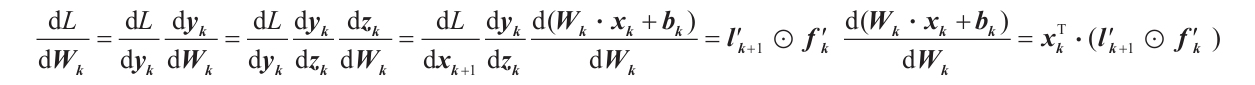
式中，l′_k+1是k+1層對輸入的導數，x_k+1=y_k，f_k′是這層激活函數的導數，x^T是x的轉置。請注意，z_k表示k層的加權和的結果（即在該層的激活函數輸入之前），其定義見1.4.1節。最后，符號表示兩個向量或矩陣之間對應元素相乘，它也被稱為哈達瑪積。如下式所示，哈達瑪積基本就是將各對應元素成對相乘：

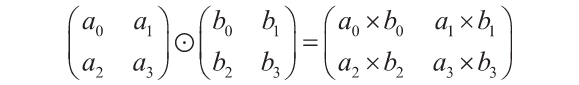
回到鏈式法則，對偏置的導數也可以用類似的方法計算：

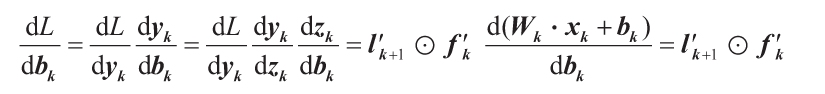
最后，為便于你能夠掌握得更加詳盡，還有以下等式：

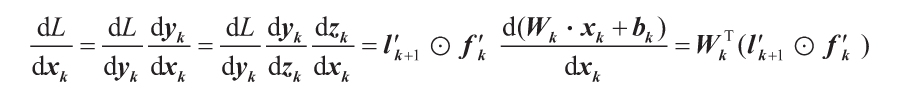
這些計算可能看起來很復雜，但我們只需要理解它們所代表的內涵——我們可以一層一層地、逆向地計算每個參數如何遞歸地影響損失（使用某一層的導數來計算前一層的導數）。我們也可以通過將神經網絡表示為計算圖，即作為數學運算的圖形鏈接在一起，來說明該概念。（執行第一層的加權求和，將其結果傳遞給第一個激活函數，然后將輸出傳遞給第二層進行操作，以此類推）。因此，計算整個神經網絡關于某些輸入的結果就包含了通過這個計算圖來前向傳遞數據，而獲得關于它的每個參數的導數則包含了將產生的損失在計算圖中的向后傳播，因此這個過程被稱為反向傳播。

為了從輸出層開始這個過程，我們需要損失本身對輸出值的導數（參考前面的方程）。因此，損失函數的推導是很容易的。例如，L2損失的導數為：

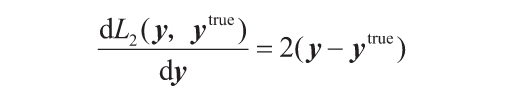
正如之前提到的，一旦知道了每個參數的損失的導數，只需要相應地更新它們即可：

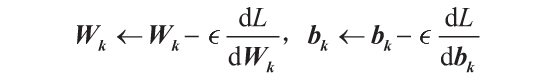
如上所示，在更新參數之前，導數通常要乘以一個因子。這個因子被稱為學習率。它有助于控制在每次迭代中更新每個參數的強度。較大的學習率可能允許網絡學習得更快，但有可能使步伐太大造成網絡錯過最小損失值。因此，應該謹慎地設置它的值。完整的訓練過程如下：

1）選擇n幅圖像用于下一次訓練并將它們輸入到網絡中。

2）利用鏈式法則求出對各層參數的導數，計算并反向傳播損失。

3）根據相應的導數值更新參數（根據學習率控制更新尺度）。

4）重復步驟1～3來遍歷整個訓練集。

5）重復步驟1～4，直到收斂或直到迭代完固定的次數為止。

整個訓練集上的一次完整迭代（步驟1～4）稱為一輪（epoch）。如果n=1，則在剩余的圖像中隨機選取訓練樣本，這個過程稱為隨機梯度下降（Stochastic Gradient Descent，SGD），它易于實現和可視化，但速度較慢（更新次數較多）、噪聲較大。人們傾向于選擇小批量隨機梯度下降（mini-batch stochastic gradient descent）。它意味著使用更多的（n更大）值（受計算機能力的限制），這時的梯度是具有n個隨機訓練樣本的每個小批（或更簡單地稱為批）上的平均梯度（這樣噪聲更小）。

如今，不管n為多少，SGD這個術語都已被廣泛使用。

在本節中，我們討論了如何訓練神經網絡。是時候把這些知識付諸實踐了！

訓練網絡分類

到目前為止，我們只實現了網絡及其層的前饋功能。首先，更新FullyConnectedLayer類，以便添加反向傳播和優化算法：

本節中提供的代碼經過了簡化，并去掉了注釋，以保持合適的長度。完整的源代碼可以在本書的GitHub庫中找到，同時還可找到一個Jupyter Notebook，它將所有內容連接在了一起。

現在，我們需要通過一層一層地加載算法以實現反向傳播和優化，并利用最終的算法來覆蓋完整的訓練（步驟1～5），因此相應地對SimpleNetwork類進行更新：

一切準備就緒！我們可以訓練神經網絡，并看看它的表現如何：

如果你的計算機有足夠的算力來完成這個訓練（這個簡單的實現沒有利用GPU），那么就將得到該神經網絡，它能夠以94.8%的準確率對手寫數字進行分類！

訓練注意事項：欠擬合和過擬合

我們邀請你嘗試一下剛剛實現的框架，嘗試不同的超參數（層大小、學習率、批大小等）。選擇合適的網絡拓撲（以及其他超參數）可能需要大量的調整和測試。雖然輸入層和輸出層的大小是由用例情況（例如，對于分類，輸入大小是圖像的像素數量，而輸出大小是待預測的類的數量）決定的，隱藏層仍應該經過精心設計。

舉例來說，如果網絡的層數太少或層太小，那么準確率可能會停滯不前。這意味著網絡是欠擬合的，也就是說，它沒有足夠的參數來處理復雜任務。在這種情況下，唯一的解決方案是采用更適合用例的新架構。

另一方面，如果網絡太復雜或訓練數據集太小，網絡可能會針對訓練數據產生過擬合。這意味著該網絡將很好地適應訓練分布（即其特定的噪聲、細節等），但不能泛化到新的樣本（因為這些新圖像可能有稍微不同的噪聲）。圖1-16展示了這兩個問題之間的區別。最左側的回歸方法沒有足夠的參數來模擬數據的變化，而最右側的方法則由于參數太多，失去了泛化能力。

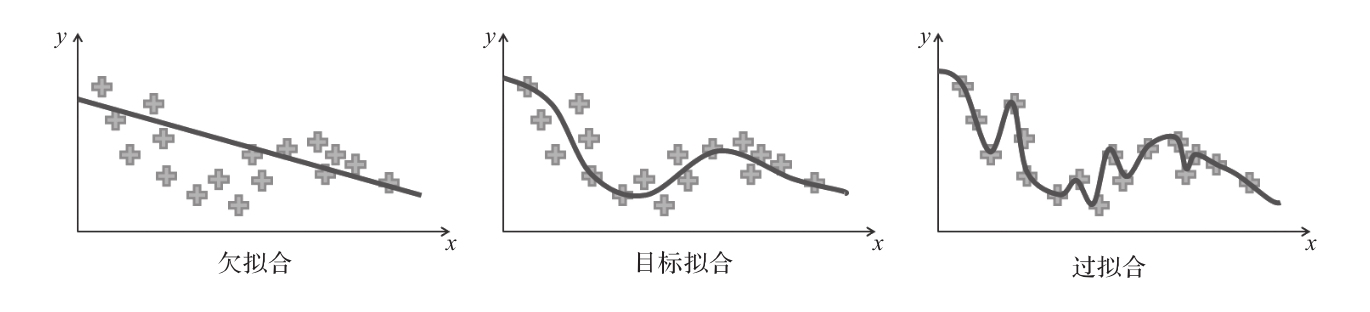
圖1-16　欠擬合和過擬合的常見示意圖

雖然收集更大、更多樣化的訓練數據集似乎是過擬合的合理解決方案，但在實踐中并不總是可行的（例如，由于目標對象存在訪問限制）。另一種解決方案是調整網絡或其訓練，以限制網絡學習的細節。這些方法將在第3章詳細介紹，屆時還會在該章介紹其他先進的神經網絡解決方案。