- Neural Network Programming with TensorFlow
- Manpreet Singh Ghotra Rajdeep Dua
- 153字
- 2021-07-02 15:17:07
Matrix multiplication
Matrix multiplication of matrices A and B is a third matrix, C:
C = AB
The element-wise product of matrices is called a Hadamard product and is denoted as A.B.
The dot product of two vectors x and y of the same dimensionality is the matrix product x transposing y. Matrix product C = AB is like computing Ci,j as the dot product between row i of matrix A and column j of matrix B:
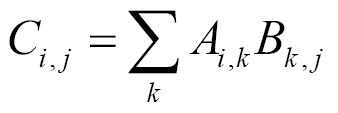
The following example shows the Hadamard product and dot product using tensor objects:
import tensorflow as tf
mat1 = tf.constant([[4, 5, 6],[3,2,1]])
mat2 = tf.constant([[7, 8, 9],[10, 11, 12]])
# hadamard product (element wise)
mult = tf.multiply(mat1, mat2)
# dot product (no. of rows = no. of columns)
dotprod = tf.matmul(mat1, tf.transpose(mat2))
with tf.Session() as sess:
print(sess.run(mult))
print(sess.run(dotprod))
The output of the listing is shown as follows:
[[28 40 54][30 22 12]]
[[122 167][ 46 64]]
推薦閱讀
- 公有云容器化指南:騰訊云TKE實戰與應用
- 程序員修煉之道:從小工到專家
- Learning Spring Boot
- MySQL從入門到精通(第3版)
- Live Longer with AI
- Mastering Machine Learning with R(Second Edition)
- 大數據Hadoop 3.X分布式處理實戰
- 智能數據分析:入門、實戰與平臺構建
- 數據挖掘原理與SPSS Clementine應用寶典
- Oracle PL/SQL實例精解(原書第5版)
- PostgreSQL指南:內幕探索
- 數據分析師養成寶典
- 大數據技術原理與應用:概念、存儲、處理、分析與應用
- Expert Python Programming(Third Edition)
- Hands-On System Programming with C++