- Hands-On Mathematics for Deep Learning
- Jay Dawani
- 262字
- 2021-06-18 18:55:08
Solving linear equations in n-dimensions
Now that we've dealt with linear equations in 2-dimensions and have developed an understanding of them, let's go a step further and look at equations in 3-dimensions.
Earlier, our equations produced curves in the 2-dimensional space (xy-plane). Now, the equations we will be dealing with will produce planes in 3-dimensional space (xyz-plane).
Let's take an arbitrary 3x3 matrix, as follows:
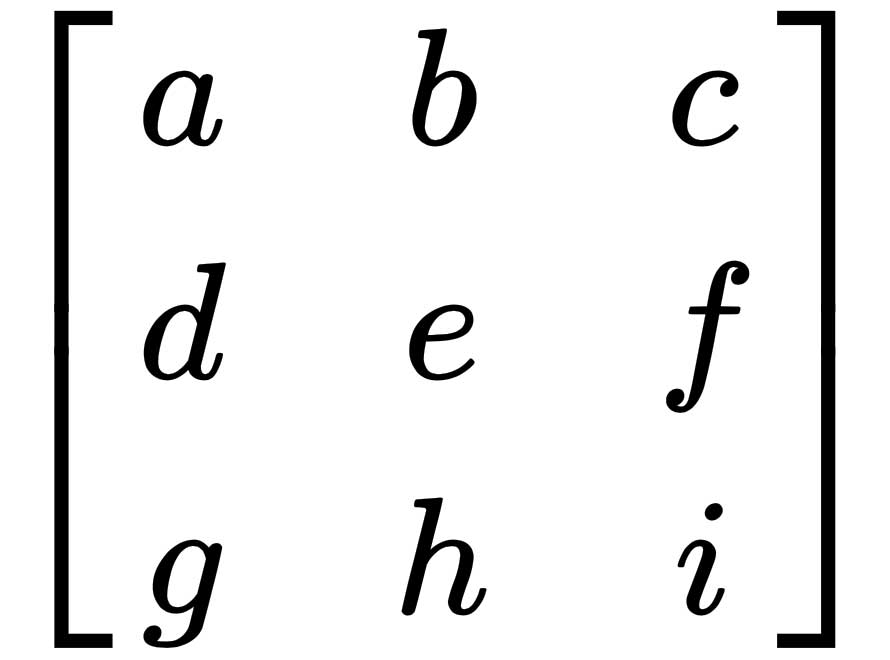
We know from earlier in having dealt with linear equations in two dimensions that our solution b, as before, is a linear combination of the three column vectors, so that 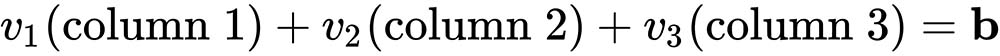 .
.
The equation  (equation 1) produces a plane, as do
(equation 1) produces a plane, as do 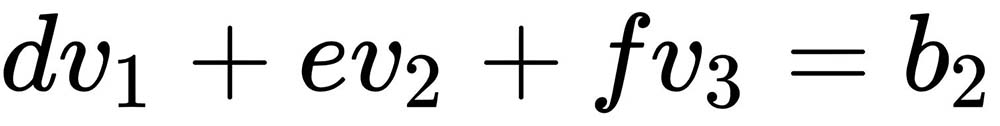 (equation 2), and
(equation 2), and 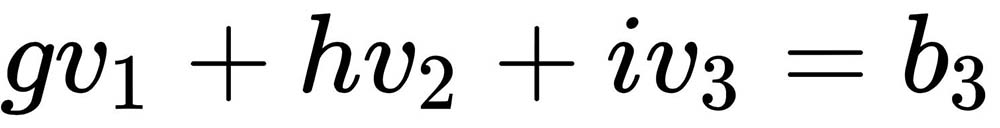 (equation 3).
(equation 3).
When two planes intersect, they intersect at a line; however, when three planes intersect, they intersect at a point. That point is the vector  , which is the solution to our problem.
, which is the solution to our problem.
However, if the three planes do not intersect at a point, there is no solution to the linear equation. This same concept of solving linear equations can be extended to many more dimensions.
Suppose now that we have a system with 15 linear equations and 15 unknown variables. We can use the preceding method and, according to it, we need to find the point that satisfies all the 15 equations—that is, where they intersect (if it exists).
It will look like this:

As you can tell, that's a lot of equations we have to deal with, and the greater the number of dimensions, the harder this becomes to solve.