2.2 群決策理論與方法

2.2.1 群決策理論

群決策理論是一門集合社會心理學、數學、行為學和決策科學等多學科領域的綜合性的交叉學科[84]，把多個決策者對于備選方案的偏好按照某種規則集結成為決策群體一致或妥協的群體偏好序的決策理論[85]。群體雖然是由多個個體構成的，但并不是每個個體決策行為的簡單加合。群決策的個體之間可以是合作的，也可以是競爭的，還可以在合作的基礎上存在競爭。由于群決策方法能夠集結多個決策參與者的偏好意見，集思廣益，能夠發揮群體智慧，減少決策中的不合理因素，消減決策者的個人偏見，更容易結合領域知識和專家經驗，使決策更加理性、準確和客觀。因此，對于群決策的理論研究被學者廣泛關注，成為眾多研究者關注的前沿問題。

群決策理論最早來自人們對社會選舉制度的探索和研究。最早的成果是1781年Borda提出的Borda計數法，用來對群體的選舉方案進行排序[86]。1785年，Condorcet更是發現了“選舉悖論”，進而制定出Condorcet規則[87]。群體決策理論除源自社會選舉理論外，福利經濟理論也是另外一個不可或缺的理論基石。福利經濟理論研究的是社會福利問題，Samuelson等人在1947年通過構建社會福利函數對各種社會福利狀況排序[88]。到1962年，諾貝爾經濟獎得主Arrow在他的著作《Social Choice and Individual Values》中提出著名的Aorrw不可能定理：沒有一個社會福利函數能同時滿足五個公理。該五個公理為：許可性、一致性、獨立性、非強制性和非獨裁性。Aorrw不可能定理為群決策的研究奠定了重要的理論基礎[89]。

在20世紀80年代后，隨著對群決策理論研究的不斷深入，各種新理論、新方法不斷地融合到群決策中，特別是效用理論和行為理論，是群決策發展中不可或缺的基石。效用理論認為決策是基于人的主觀考慮，可以用概率來反映人的主觀思想及其不確定性，通過建立效用函數來表達群體的偏好結構，并評估決策方案的優先次序[90]。行為理論是從認知心理學的角度，分析個體決策行為的心理，以統計決策理論為框架，著重于研究決策的非理性行為[91]。

目前，群決策理論已經形成了一個較完整的體系架構，涉及多個領域：群體效用理論、行為理論、多目標群決策理論、模糊群體決策理論以及群決策支持系統等[92]。但由于進行群決策時，存在決策參與者眾多，效率可能低下，因決策者的知識、背景、經驗不同而造成決策結果也往往不同，以及交互式決策不可重復、易受某一個權威專家影響等問題，因此，對群決策理論的研究和豐富還有很大空間。

2.2.2 群決策方法

2.2.2.1 Borda函數法

Borda提出的Borda函數法是：由每個投票人對m個候選人進行排序，排在第一位的得m-1分，排在第二位的得m-2分，然后統計各候選者所得分大小，根據各候選人所得總分確定其排序。

Borda函數定義為：

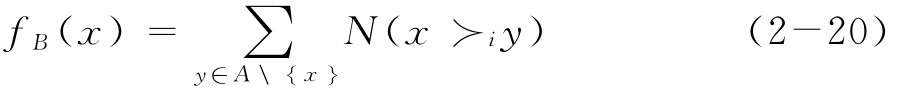
fB（x）是候選人x與其他候選人逐一比較m-1次所得票數的總和，各候選人按fB（x）值的大小確定其優劣[92]。

2.2.2.2 Condorcet函數法

Condorcet函數法認為：當從眾多個候選人中選擇某一個時，首先對候選人進行成對的比較，若某個候選人能按過半數的規則擊敗其他的所有候選人，則可稱為Condorcet候選人，應該由他當選；如果不存在，則應按Condorcet函數fc（x）值的大小來排列候選人x的優劣次序。fc（x）是一種極大化極小函數，它是候選人x與其他所有候選人逐一比較時得票最少的那一次的所有票數[92]。

Condorcet函數的定義為：

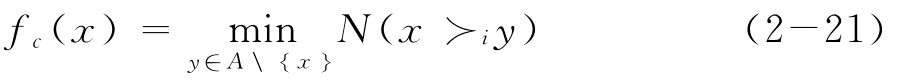
2.2.2.3 逼近于理想解的群排序方法

逼近于理想解的群排序方法，是指借助于多目標決策問題中逼近理想解排序方法（TOPSIS）中的“理想解”和“負理想解”對群體的決策方案進行排序。在使用時，需要在目標空間中定義一測度去測量某個方案靠近理想解和遠離負理想解的程度，一般采用歐式距離[92]度量。具體步驟如下：

（1）計算標準化決策矩陣：

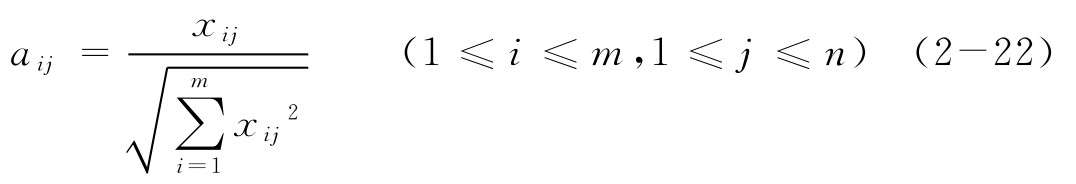
（2）計算第k位專家的加權決策化矩陣：

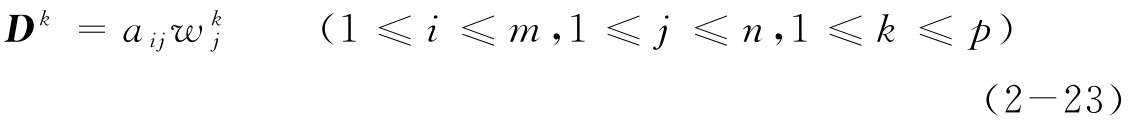
其中是第k位專家關于第j個指標的權重，并且= 1。

（3）計算加權的群決策判斷矩陣：

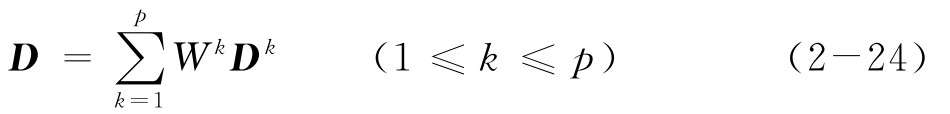
這里的Wk是第k個專家的專家權重，主要考慮每個專家的專家意見的權威性，并且= 1。

（4）計算群體理想解V*和群體負理想解V-：

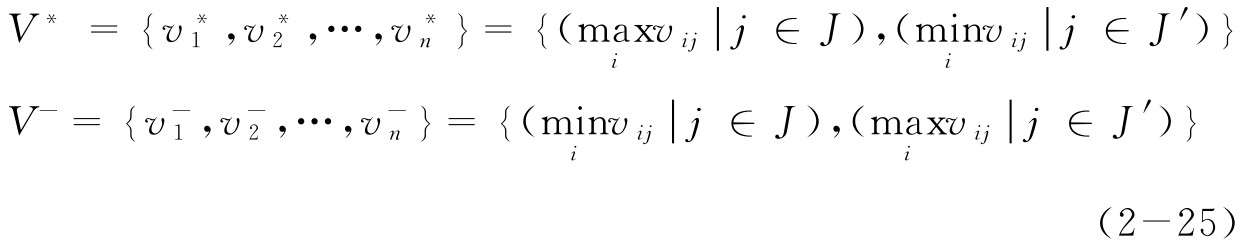
（5）計算備選方案到理想解、負理想解的相對距離，按歐式距離計算：

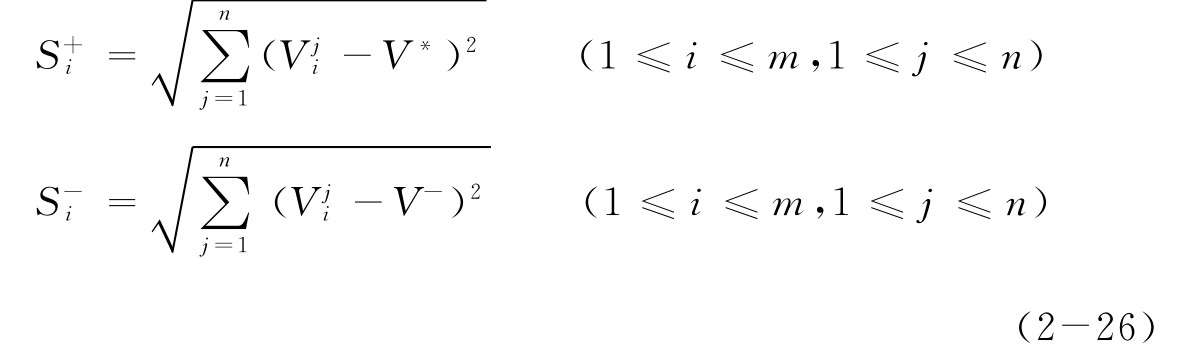
（6）計算各備選方案的相對貼近度：

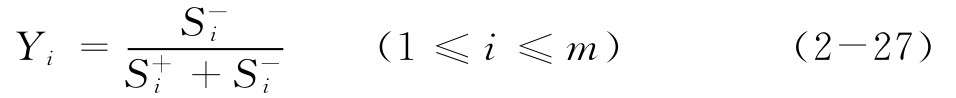
Yi越接近1，說明備選方案就越接近理想方案。

（7）根據相對貼近度的大小對備選方案排序。相對貼近度的值越大，方案越好。

2.2.2.4 Delphi法

德爾斐（Delphi）法又稱專家咨詢法，是指就一定的問題函請相關領域的專家提出意見或看法，然后將專家的答復意見或新設想加以科學地綜合、整理、歸納，以匿名的方式將所歸納的結果反饋給各專家再次征詢意見[92]。德爾斐法由三個要素組成：一是一名協調人；二是一群與決策問題有關的專家；三是一套特制的征詢調查表和程序。具體步驟如下：

（1）編制專家咨詢表。根據評價指標、評價內容和必要的填表說明，繪制專家咨詢表格。

（2）專家對目標問題提出自己的初步看法和意見。專家們首先根據自己的知識經驗和對評價對象的初步了解，填寫專家咨詢表，然后組織者收回表格，并在第一時間進行歸類、整理，之后設計出新的咨詢表，并以匿名的方式將所歸納的結果再分發給專家。

（3）再次征詢專家對目標問題的看法和意見。這一輪要求各位專家給出自己的意見和建議同時說明理由。收回咨詢表后，組織者第一時間對專家意見進行歸類、處理，將整理后的數據設計出新的咨詢表作為第三輪調查表，并以匿名的方式將所歸納的結果再次反饋給專家。

（4）專家根據反饋信息，再一次作出判斷并提出修改意見。組織者設計第四輪的專家咨詢表，并以匿名的方式將所歸納的結果再次分發給專家。

（5）在第三輪的基礎上，專家再次進行判斷或保留第三輪的意見。Delphi法一般至少需要經過4輪咨詢專家意見。

（6）結果處理。對專家應答的結果進行統計分析。

2.2.2.5 Nash談判模型

Nash談判模型是一種用公理化方法解決談判問題的策略分析模型，屬于完全信息條件下的利益分配博弈模型[93-94]。在求解Nash談判模型時，首先有如下假設：

（1）每個人都希望對方是合乎理性的。

（2）談判雙方的效用函數能足夠精確地反映各自的偏好。

（3）任何協議一經達成，就具有強制性，不得違約。

為了能夠求得談判結果，Nash還提出了以下公理[92]：

公理1可行性公理：后果限于談判集內，談判雙方一致達成的協議點是談判集中的可行點，是Pareto最優的，且不劣于現狀點。

公理2對稱性公理：如果可行域R是對稱的，即現狀點是對稱的，則達成的協議也是對稱的。

公理3策略上等價表示的不變性公理：如果原談判問題中的效用μ1（·）和μ2（·）經正線性變換得到μ′1=α1μ1+β1和μ′2=α2μ2+β2，構成新的判斷問題，且原問題的協議點是（x*, y*），則新的談判問題的協議點是（α1x*+β1, α2x*+β2）。此公理意為在求解談判問題時不必對雙方的偏好強度做人際比較，同時可以對談判問題作坐標變換，使之規范化后再求解。

公理4無關方案獨立性公理：設有兩個談判問題，若第二個談判問題的可行域R2是第一個談判問題的可行域R1的子集，即R2?R1。兩個問題的現狀點相同，均為（xc, yc），且（xc, yc）?R2，則第一個談判問題的協議點（x*, y*）?R2，即（x*, y*）也是第二個談判問題的協議點。

在這些公理的基礎上，Nash給出了如下定理：

定理1若公理1到公理4成立，且R中存在x ≥xc, y ≥yc的點，則（x*, y*）唯一，它使定義在R上的函數（x -xc）（y -yc）取極大值[92]。

更一般地，對n≥2的多人談判問題，Nash談判模型為

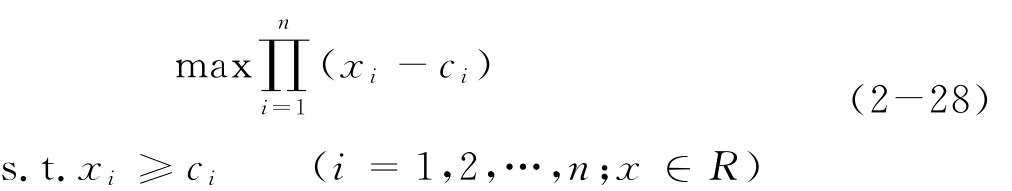
其中ci為談判人i的現狀值，xi為談判者i的后果，R是可行域。上述模型的解稱做Nash平衡解[92]。