2.1 多目標(biāo)決策理論與方法

2.1.1 多目標(biāo)決策理論

多目標(biāo)決策理論是運(yùn)籌學(xué)的一個(gè)活躍且具有挑戰(zhàn)性的分支領(lǐng)域，其依據(jù)決策背景，綜合考慮多個(gè)相互間可能存在分歧甚至矛盾的評價(jià)指標(biāo)，利用統(tǒng)計(jì)學(xué)原理、運(yùn)籌學(xué)方法、管理學(xué)理念以及最優(yōu)化理論，對多個(gè)備選方案進(jìn)行選優(yōu)和排序的方法理論體系[31,63]。備選方案的選擇取決于多個(gè)目標(biāo)或多個(gè)評價(jià)指標(biāo)的滿足程度。多目標(biāo)決策問題最早由意大利的經(jīng)濟(jì)學(xué)家帕累托提出[64-65]。之后，1951年Kuhn和Tukcer利用數(shù)學(xué)規(guī)劃模型來研究目標(biāo)函數(shù)極大化問題，并給出了“有效解”存在的最優(yōu)條件，該“有效解”被稱為Kuhn-Tukcer有效解[54]。到20世紀(jì)60年代，學(xué)術(shù)界逐漸地出現(xiàn)了很多解決多目標(biāo)決策問題的方法。但直到20世紀(jì)70年代，多目標(biāo)決策理論才受到廣大學(xué)者的持續(xù)關(guān)注，有了快速的發(fā)展，并取得了較大的成果。在使用多目標(biāo)決策方法評估實(shí)際問題時(shí)，通常需要從以下五個(gè)方面進(jìn)行分析：目標(biāo)問題的明確、決策者的選定、評價(jià)指標(biāo)體系的建立、決策判斷矩陣的構(gòu)建和屬性權(quán)重的確定[66-67]。其中，對于給定的目標(biāo)問題，評價(jià)結(jié)果的準(zhǔn)確性很大程度上取決于屬性權(quán)重的確定。

其實(shí)，決策無處不在。不論是在專業(yè)領(lǐng)域，還是在日常生活的管理和決策中，我們常常都能夠接觸到相互矛盾的指標(biāo)。比如質(zhì)量和成本指標(biāo)，提高質(zhì)量，往往伴隨著成本的增加；降低成本，又往往伴隨著以犧牲質(zhì)量為潛在代價(jià)。又如預(yù)期收益和風(fēng)險(xiǎn)指標(biāo)，追求高收益的產(chǎn)品，往往伴隨著高風(fēng)險(xiǎn)；購買低風(fēng)險(xiǎn)的產(chǎn)品，收益又往往很不理想。面對真實(shí)情況的復(fù)雜問題該如何科學(xué)地進(jìn)行決策，是擺在學(xué)者面前的高挑戰(zhàn)性難題。正是基于如此的研究背景和問題導(dǎo)向，學(xué)者們才不斷地關(guān)注多目標(biāo)決策領(lǐng)域，并建立了多種經(jīng)典的多目標(biāo)決策方法，如層次分析法（AHP）、數(shù)據(jù)包絡(luò)分析法（DEA）、逼近于理想解的排序方法（TOPSIS）、選擇轉(zhuǎn)換本質(zhì)法（ELECTRE）、偏好順序結(jié)構(gòu)評估法（PROMETHEE）、灰色關(guān)聯(lián)分析法（GRA）、簡單線性加權(quán)求和法（WSM）、多準(zhǔn)則妥協(xié)解排序法（VIKOR）等[68-72]。

2.1.2 多目標(biāo)決策方法

2.1.2.1 層次分析法（AHP）

AHP（Analytical Hierarchy Process）由美國運(yùn)籌學(xué)家Saaty在20世紀(jì)70年代提出，是一種綜合定量評估與定性研究的通過結(jié)構(gòu)建模和兩兩對比判斷矩陣進(jìn)行多目標(biāo)決策分析的方法[36-37]。其基本思想是，首先把目標(biāo)問題系統(tǒng)化、層次化，建立層次結(jié)構(gòu)模型，然后結(jié)合專家意見，構(gòu)建兩兩對比判斷矩陣，通過科學(xué)化計(jì)算，導(dǎo)出方案的優(yōu)先級向量進(jìn)行優(yōu)選和排序[37]。具體的計(jì)算步驟如下：

（1）分析問題，確定層次目標(biāo)。針對復(fù)雜的現(xiàn)實(shí)問題，抽象、歸納出待解決的目標(biāo)問題。

（2）構(gòu)建決策層級結(jié)構(gòu)。對目標(biāo)問題根據(jù)一定的規(guī)則進(jìn)行分解，形成包括目標(biāo)層、準(zhǔn)則層和方案層的決策層級結(jié)構(gòu)。

（3）建立兩兩對比決策矩陣。根據(jù)1-9標(biāo)度法，通過專家咨詢，結(jié)合領(lǐng)域知識(shí)和專家意見，對每一層級結(jié)構(gòu)中的兩兩指標(biāo)相對重要性進(jìn)行打分，建立兩兩對比決策矩陣。

（4）層次單排序。計(jì)算兩兩對比決策矩陣的最大特征值和特征向量，進(jìn)行層次單排序。

（5）一致性檢驗(yàn)。根據(jù)一致性比率進(jìn)行一致性檢驗(yàn)。若一致性比率小于0.1，檢驗(yàn)通過，特征向量即為權(quán)向量；若一致性比率大于0.1，檢驗(yàn)不通過，則需重新構(gòu)造兩兩對比判斷矩陣。

（6）層次總排序。根據(jù)層次單排序的計(jì)算結(jié)果，進(jìn)行層次總排序，得出方案層相對于目標(biāo)層的組合權(quán)重，權(quán)重的大小則對應(yīng)了各方案的優(yōu)劣。

2.1.2.2 逼近理想解排序法（TOPSIS）

TOPSIS最早由Hwang和Yoon在1981年提出[73]，是一種根據(jù)距離函數(shù)進(jìn)行目標(biāo)搜尋的方法。該方法首先計(jì)算出評估方案中的正理想解和負(fù)理想解，然后根據(jù)備選方案到正理想解、負(fù)理想解的相對距離（一般采用歐式距離）對備選方案進(jìn)行優(yōu)選[74]。具體步驟如下：

（1）計(jì)算標(biāo)準(zhǔn)化矩陣A。決策矩陣標(biāo)準(zhǔn)化，得標(biāo)準(zhǔn)化決策矩陣A：

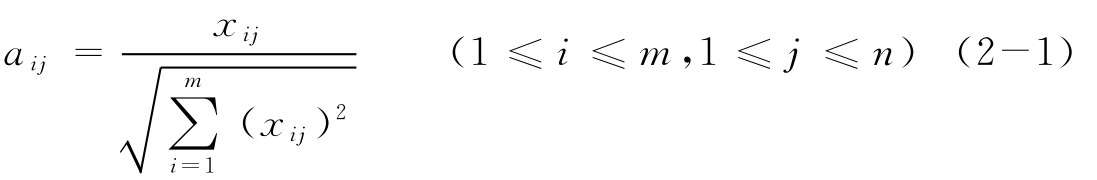
（2）計(jì)算加權(quán)標(biāo)準(zhǔn)化決策矩陣：

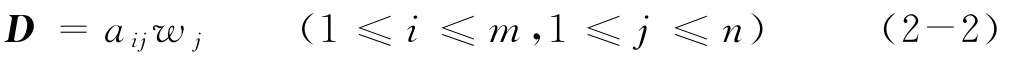
其中wj是第j個(gè)指標(biāo)的權(quán)重，并且= 1。

（3）計(jì)算理想解V*和負(fù)理想解V-：

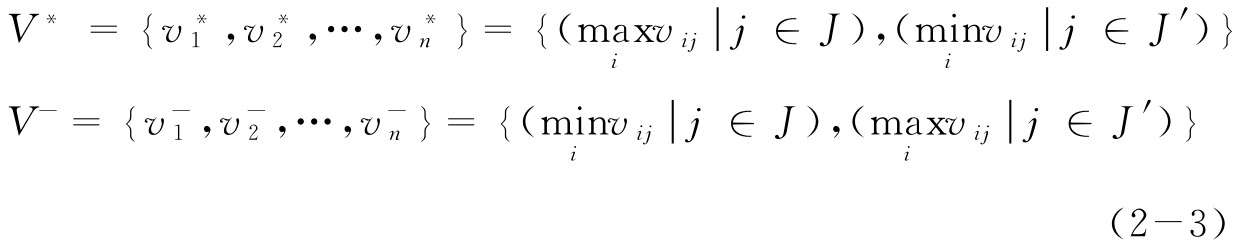
（4）計(jì)算備選方案到正理想解、負(fù)理想解的相對距離，按歐式距離計(jì)算：

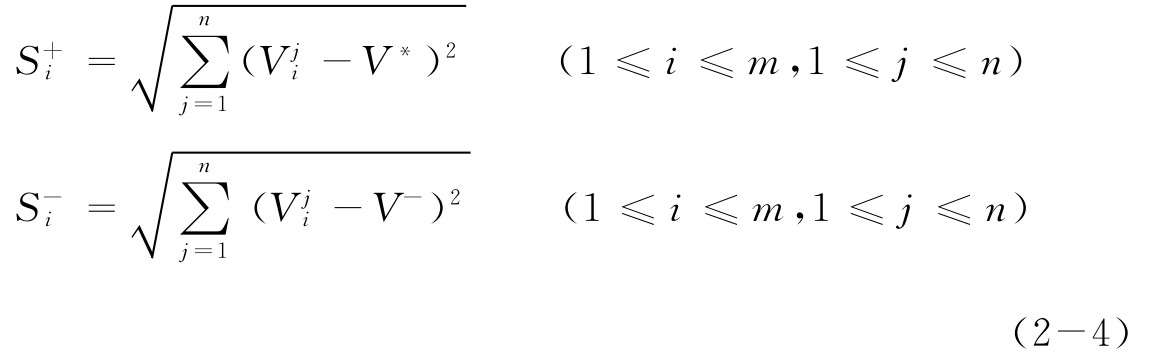
（5）計(jì)算各備選方案的相對貼近度：

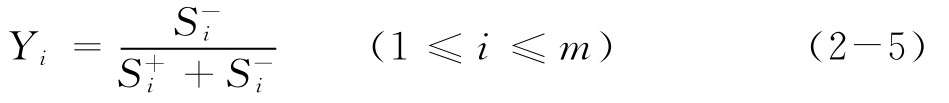
其中Yi∈（0,1）, Yi越接近1，備選方案就越接近理想解。

（6）根據(jù)相對貼近度的大小對備選方案排序。相對貼近度的值越大，方案則越好。

2.1.2.3 灰色關(guān)聯(lián)分析法（GRA）

GRA（Grey Relational Analysis）由Deng在1988年提出，是一種用灰色關(guān)聯(lián)度來描述方案之間發(fā)展趨勢關(guān)系或相異程度的多因素統(tǒng)計(jì)分析方法[75]。評估步驟如下：首先，對目標(biāo)方案建立可比性序列，并從中確定一個(gè)理想的目標(biāo)序列；然后，計(jì)算備選方案與理想目標(biāo)序列間的灰色關(guān)聯(lián)系數(shù)；最后，計(jì)算灰色關(guān)聯(lián)度，并據(jù)此對備選方案進(jìn)行排序[76]。具體步驟如下：

（1）假設(shè)初始的判斷決策矩陣為R，構(gòu)建標(biāo)準(zhǔn)化決策矩陣R′：

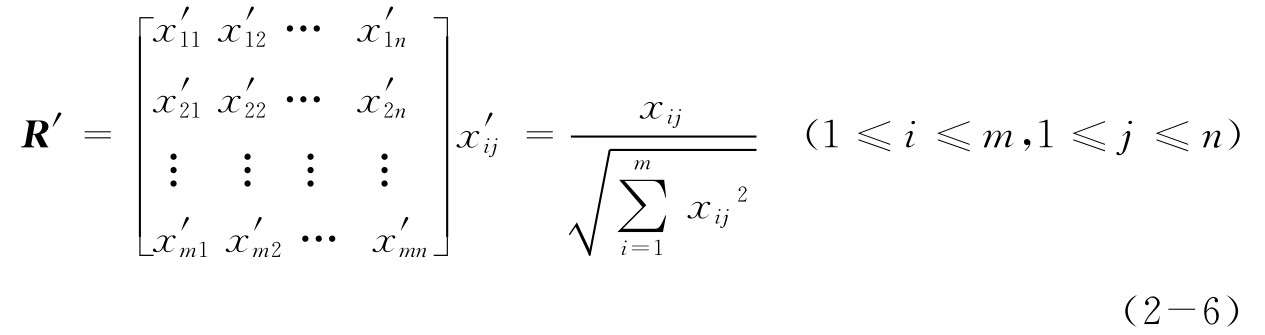
（2）生成參考序列：

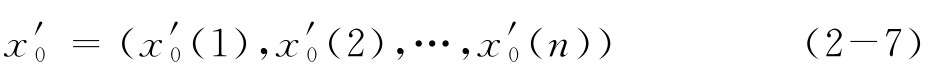
（j）是標(biāo)準(zhǔn)化后第j個(gè)指標(biāo)的最大值。

（3）計(jì)算標(biāo)準(zhǔn)化后的序列與參考序列的差異度Δ0i（j）：

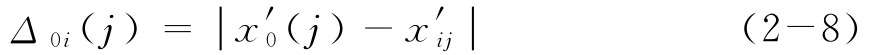
并構(gòu)建差異度矩陣：

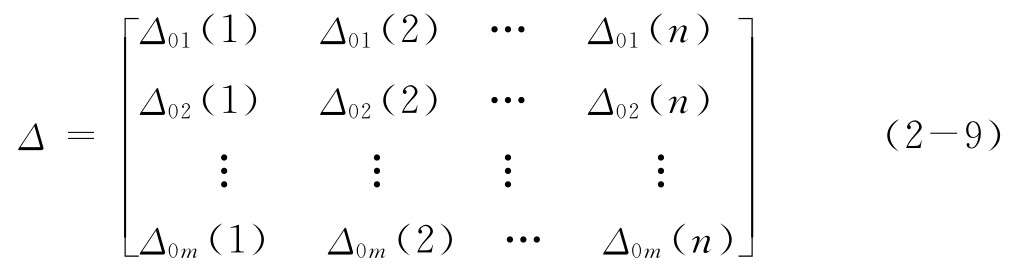
（4）計(jì)算灰色關(guān)聯(lián)系數(shù)r0i（j）：

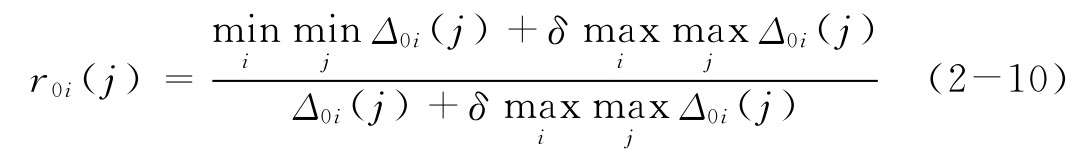
其中δ是一個(gè)分辨系數(shù)，其值常設(shè)為0.5。

（5）計(jì)算灰色關(guān)聯(lián)度bi：

最后，根據(jù)灰色關(guān)聯(lián)度對備選方案排序，值越大越好。

2.1.2.4 偏好順序結(jié)構(gòu)評估法（PROMETHEE）

PROMETHEE是由Brans和Landry于1982年提出的，通過計(jì)算備選方案效用的流入量、流出量及凈流量，根據(jù)凈流量的大小對評估方案進(jìn)行排序[77]。目前，PROMETHEE法已有了多種擴(kuò)展方法，如PROMETHEE Ⅰ、PROMETHEE Ⅱ、PROMETHEE Ⅲ、PROMETHEE TRI、PROMETHEE Ⅳ、PROMETHEE Ⅴ[78]。PROMETHEE Ⅰ/Ⅱ法是決策者根據(jù)自己的偏好為每一準(zhǔn)則選擇偏好函數(shù)，利用偏好函數(shù)和準(zhǔn)則權(quán)系數(shù)，定義兩方案的偏好優(yōu)序指數(shù)，進(jìn)而求出備選方案效用的流入量、流出量及凈流量，并根據(jù)凈流量的大小對評估方案的一個(gè)部分或整體排序。其評估步驟如下[79]：

假設(shè)有n個(gè)備選方案，m個(gè)評價(jià)準(zhǔn)則，g為在評價(jià)準(zhǔn)則下的評估函數(shù)，令兩個(gè)備選方案A和B在同一個(gè)評價(jià)準(zhǔn)則下相比較，結(jié)果有：

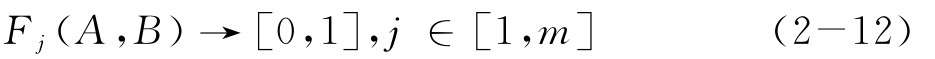
Brans和Landry給出了6種偏好函數(shù)，并且定義如下參數(shù)：q為無差異閾值，p為絕對偏好閾值，s是介于p和q之間的一個(gè)值，則：

若Fj（A, B）=0，則gj（A）-gj（B）≤qj，說明A與B之間無優(yōu)劣之分；

若Fj（A, B）=1，則gj（A）-gj（B）≥pj，說明A相對于B有絕對的偏好；

若0＜Fj（A, B）＜1，則qj≤gj（A）-gj（B）≤pj，說明A相對于B有較強(qiáng)的偏好。

然后，定義多準(zhǔn)則偏好指標(biāo)：

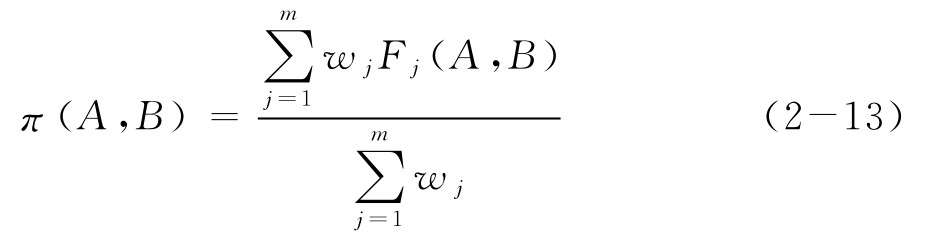
其中wj為評價(jià)準(zhǔn)則的權(quán)重，π（A, B）是決策者在評估準(zhǔn)則下方案A相對于方案B的偏好程度。

然后，確定備選方案的流出量、流入量：

流出量：φ+（A）=∑B∈Kπ（A, B）（A ∈n），用來描述方案A相對于其他方案的偏好程度；

流入量：φ-（A）=∑B∈Kπ（B, A）（A ∈n），用來描述其他方案相對于方案A的偏好程度。

然后，可得凈流量：

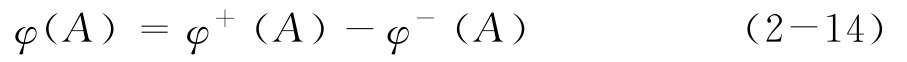
根據(jù)凈流量的大小進(jìn)行方案排序。凈流量越大的方案越好。

2.1.2.5 多準(zhǔn)則妥協(xié)解排序法（VIKOR）

VIKOR是Opricovic于1998年提出的一種探索和尋找折中方案的多目標(biāo)決策方法[81]。VIKOR通過引入妥協(xié)解對存在矛盾或沖突的評價(jià)指標(biāo)進(jìn)行評估，選擇距離理想解最為接近的折中妥協(xié)解為最佳的決策方案[82]。

首先，界定理想解與負(fù)理想解。所謂理想解，是指備選方案中最好的解，它的各屬性、目標(biāo)值都達(dá)到每個(gè)候選方案中最好的值；所謂負(fù)理想解，是指備選方案中最壞的解，它的各屬性、目標(biāo)值都達(dá)到每個(gè)候選方案中最差的值。然后，引入妥協(xié)解。最后，比較各備選方案的評估值[82]。具體步驟如下：

（1）找出各備選方案的理想解和負(fù)理想解：

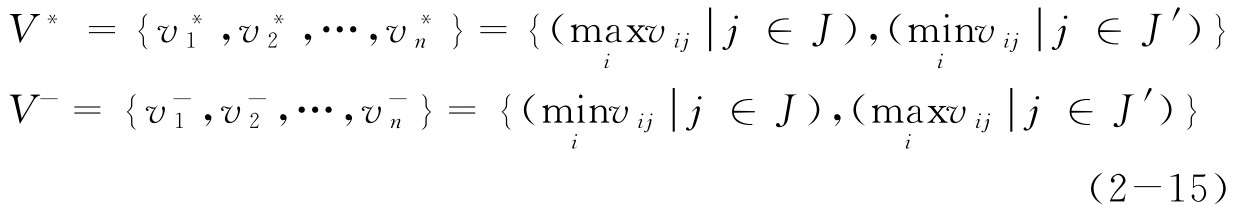
（2）計(jì)算各備選方案的加權(quán)效用值Si和最大準(zhǔn)則損失值Ri：

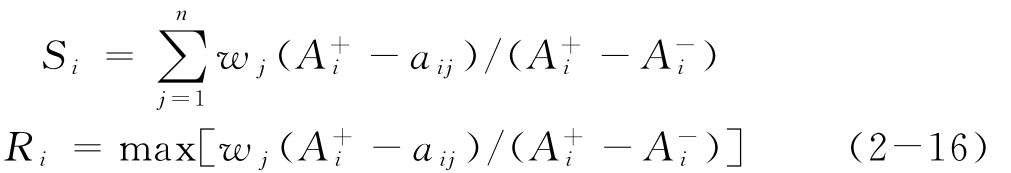
（3）根據(jù)決策者的偏好參數(shù)v，計(jì)算各方案的綜合效用值Qi：

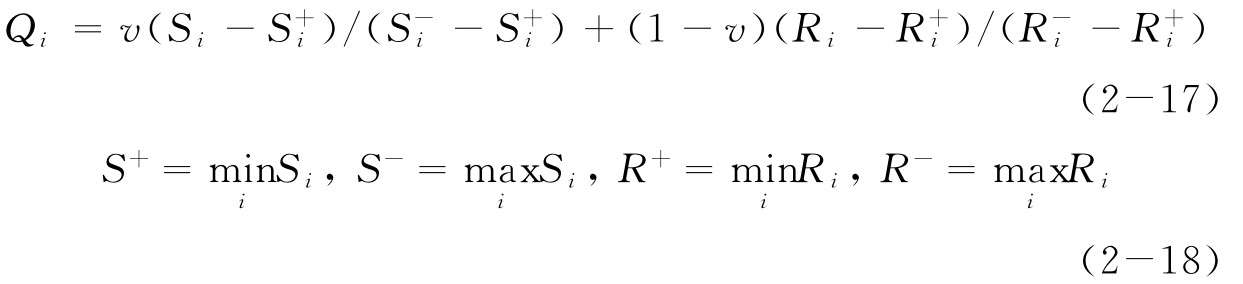
其中v是決策機(jī)制系數(shù)，一般取值為0.5。

（4）根據(jù)各備選方案的Si, Ri, Qi的關(guān)系進(jìn)行方案排序：

①如果Q（a″）-Q（a′）≥1/（m-1）且對應(yīng)的Si或Ri值也最小，則a′為最優(yōu)方案。

②如果Q（a″）-Q（a′）≥1/（m-1）且對應(yīng)的Si和Ri值均不為最小，則最優(yōu)方案為a′和a″的組合。

③如果Q（a″）-Q（a′）＜ 1/（m-1），則輸出前M個(gè)滿足Q（aM）-Q（a′）＜1/（m-1）的備選方案，同時(shí)也說明這些方案比較接近。

2.1.2.6 簡單線性加權(quán)法（WSM）

簡單線性加權(quán)法（Weighted Sum Method, WSM）理解容易，計(jì)算簡單，運(yùn)用方便。評估步驟如下：首先，獲得目標(biāo)方案的屬性值；然后，確定評價(jià)準(zhǔn)則的權(quán)重信息；最后，通過加權(quán)求和得到各方案的評估值，根據(jù)其大小對目標(biāo)方案進(jìn)行排序[83]。計(jì)算公式如下：

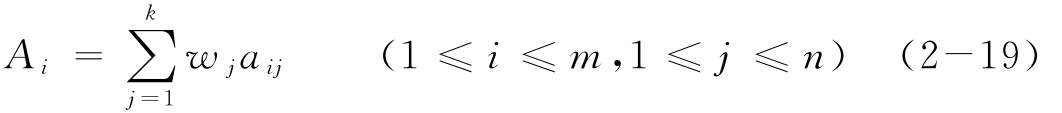
在評估過程中，Ai值越大，方案越好。