- 財(cái)務(wù)管理(雙語)
- 韓衛(wèi)華
- 822字
- 2021-04-02 19:47:56
3.2 FV and PV
How much is $1 invested today worth in the future? Here comes the future value(terminal value), which is the amount to which an investment will grow after earning interest.Similarly, we all realize that a dollar today is worth more than a dollar to be received one, two, or three years from now. Calculating the present value(discounted value)of future cash flows allows us to place all cash flows on a current footing so that comparisons can be made in terms of today's dollar.
3.2.1 FV and PV of Single Cash Flow
折現(xiàn)是指將未來收入折算成等價(jià)的現(xiàn)值。
Figure 3.1 is the timeline showing a single cash flow that occurs over a period of time.

Figure 3.1
To find out how much an amount of P(principal, or the value at present time)worth in the future, we need to do compounding to figure out the future value ofP:
FVn=PV×(1+i)n
Where,i=discount rate;n=number of period
Alternatively, we can simply find(1+i)n-FV factor, on the FV Table, which shows future value of $1 at interest rate of i for n periods.
By rearranging the FV formula, the present value of a future cash flow is calculated by discounting:
PV=FVn×(1+i)-n

Figure 3.2
Alternatively, the PV factor,(1+i)-n, can be found in PV Table, which shows present value of $1 per period at interest rate of i for n periods.
Example 3.1
Eric recently invested on a 3-year, $10000 saving note with 6% compound annual interest rate. How much will Eric receive at the end of 3 years?
Solution
FV3=$10000×(1+6%)3=$11910
Eric will receive the principal plus interest, totaling $11910 at the end of three years.
Example 3.2
On a contract you have a choice of receiving $25000 three years from now, or $35000 six years from now. If the required rate of return is 10%, what would you opt to?
Solution
To compare the value of cash flow occurs at different time, we need to adjust them to the same point of time.
The PV of $25000 three years from now is:
PV=$25000×(1+10%)-3=$18782.9
The PV of $35000 six years from now is:
PV=35000×(1+10%)-6=$19756.6
Thus, the latter option seems to have higher value.
Example 3.3
Suppose you invest $1000 in a savings account that compounds 6% annually, and you want to withdraw your savings in 15 months. How much would you withdraw?
Solution
You want to withdraw in 15 months(i.e.,1.25 years), so you can withdraw the following amount:
FV1.25=$1000×(1+6%)1.25=$1075.55
3.2.2 FV and PV of Multiple Cash Flows
多次發(fā)生的一系列款項(xiàng)
So far we have discussed the FV and PV of a single cash flow. Many time value of money problems we face involve the cash flows that occur more than once over a period of time. For example, mortgage loan requires monthly repayments over a period of 20 years-a total of 240 repayments, investment on insurance are normally paid by installment.
Illustration 3.2
Suppose Mrs. Wang was planning to invest in insurance for her 12-year-old daughter. The insurance requires the first installment of $1000 paid now and followed by other two in the next following years, $2000 and $5000 respectively. How much will the insurance be worth at the time when her daughter enters college at the age of 18, and when she graduates at 22?
The cash flows stream of the insurance looks like:
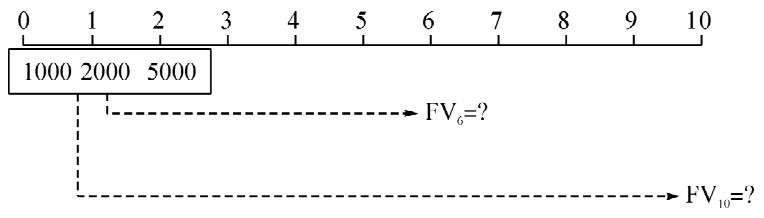
Figure 3.3
While it is not valid to add up each cash flow that occur at different times, each cash flow should be discounted/compounded individually to the same point of time before being sum up.
Example 3.4
An investment promises to offer $1000 annually at the end of years 1 and 2, followed by annual $5000 at the end of years 3 and 4, and with a final payment of $2000 at the end of year 5. Suppose the investor requires 12% annual rate of return.
(a)At what price should the investor pay for this invest-ment?
(b)What is the investment worth at the end of 5 years?Solution
(a)PV=1000×(1+12%)-1+1000×(1+12%)-2+5000×(1+12%)-3+5000×(1+12%)-4+2000×(1+12%)-5
=$9561.4
The investor is willing to pay $9561.4 now for this investment.
(b)FV=1000×(1+12%)4+1000×(1+12%)3+5000×(1+12%)2+5000×(1+12%)1+2000
=$16850.45
This investment is worth $16850.45 at the end of five years.
- 財(cái)務(wù)管理(雙語)
- 職業(yè)生涯規(guī)劃實(shí)操手冊
- 新聞英語導(dǎo)讀
- 文化資源概論
- 秘書學(xué)
- 服務(wù)外包企業(yè)戰(zhàn)略管理(廣東外語外貿(mào)大學(xué)國際服務(wù)外包人才培訓(xùn)系列教材)
- 福建師范大學(xué)外國語學(xué)院211翻譯碩士英語[專業(yè)碩士]歷年考研真題及詳解
- 2020年河南公務(wù)員錄用考試專項(xiàng)教材:數(shù)量關(guān)系【考點(diǎn)精講+典型題(含歷年真題)詳解】
- 通信用戶線路終端安裝與維護(hù)
- 企業(yè)碳中和管理
- 黃甫全《現(xiàn)代課程與教學(xué)論學(xué)程》筆記和課后習(xí)題詳解
- 紡織材料學(xué)(第4版)
- 工程項(xiàng)目投標(biāo)決策機(jī)制研究
- 汽車服務(wù)企業(yè)管理(第2版)
- 計(jì)算機(jī)網(wǎng)絡(luò)實(shí)驗(yàn)指導(dǎo)