- 薛定宇教授大講堂(卷Ⅳ):MATLAB最優化計算
- 薛定宇
- 3982字
- 2020-04-24 14:21:30
2.3 代數方程的數值求解
前面介紹的圖解方法只是非線性方程組眾多求解方法的一種,圖解法有其明顯的優勢,但也有劣勢。圖解法只能用于求解一元或二元方程的實數根,對多元方程是不能采用圖解法求解的。本節將探討一般方程的求解思路與實用求解函數。
2.3.1 Newton–Raphson迭代方法
為簡單起見,可以先探討一元方程的求解方法。Newton–Raphson迭代方法是以英國科學家Isaac Newton與英國數學家Joseph Raphson(約1648?約1715)命名的一般方程的迭代方法。
假設一元方程是由f(x)=0描述的,且在x=x0點處函數的值f(x0)為已知的。這樣,可以在(x0,f(x0))點作函數曲線的一條切線,如圖2-8所示,則該切線與橫軸的交點x1可以認為是找到的方程的第一個近似的根。由圖2-8給出的斜率為f′(x0)的切線方程,可以得出x1的位置為

式中,f′(x0)為f(x)關于x的導函數在x0點的值。再由x1出發作切線,則可以得出x2,以x2出發找到x3,…。若已經找到了xk,則從該點出發可以搜索到下一個點。
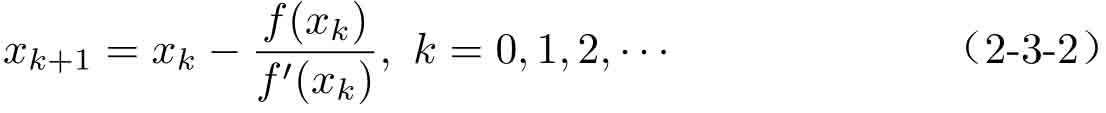
如果|xk+1?xk|≤ε1或|f(xk+1)|≤ε2,其中,ε1與ε2為預先選定的誤差容限,則可以認為xk為原方程的一個解。
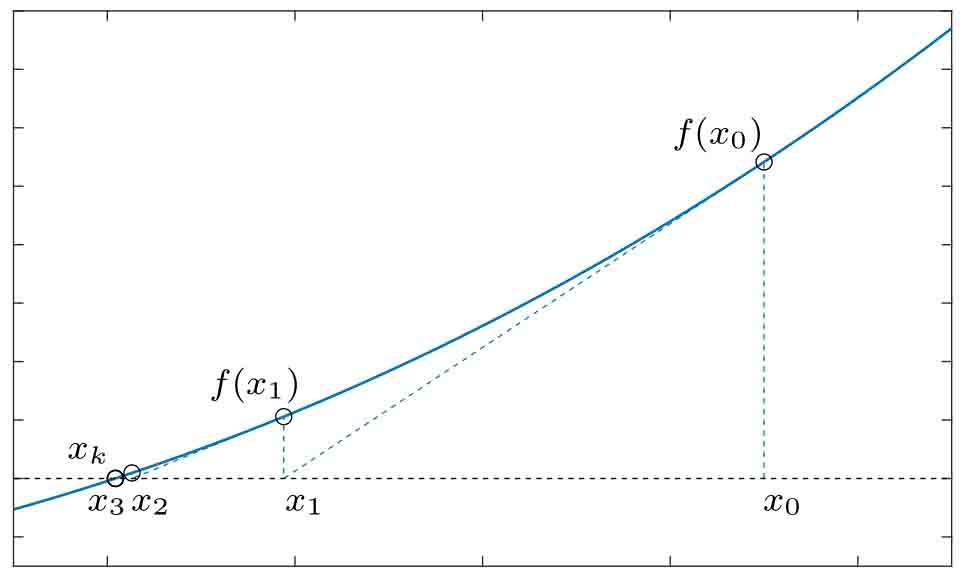
圖2-8 Newton–Raphson迭代法示意圖
定義2-7 對多元向量函數f(x),其Jacobi矩陣的定義為
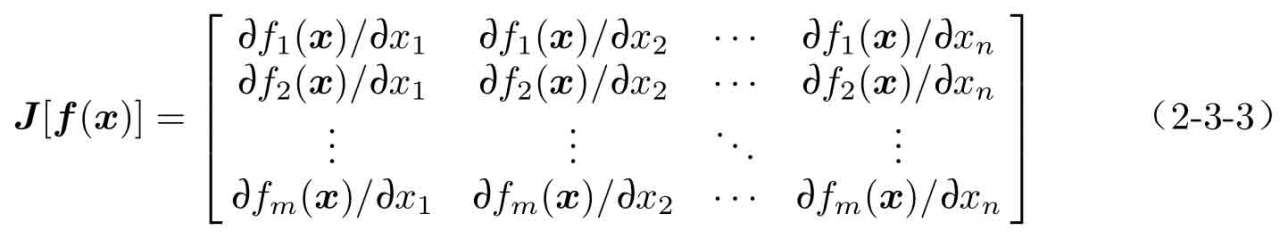
定理2-3 更一般地,對多元方程f(x)=0,其中x為向量或矩陣,而非線性函數f(x)也是同維數的函數,則可以由下式迭代求出:
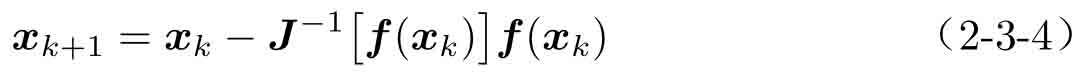
如果||xk+1?xk||≤ε1或||f(xk+1)||<ε2,則xk為方程的根。在定義中使用了Jacobi矩陣。
根據給出的算法,編寫出MATLAB的通用求解函數:

該函數需要用戶提供方程函數句柄f及其Jacobi矩陣的句柄d,還需要給出初值的列向量x0,并給出誤差限ε。如果給出key,并令其值為1,則可以將中間搜索結果由x矩陣返回。
對單變量函數而言,如果需要提供給定函數的導函數本身就是個比較麻煩的事,使用可以考慮采用正割方法來近似函數的導數,搜索方程的根。這時,求解式(2-3-2)可以改寫成
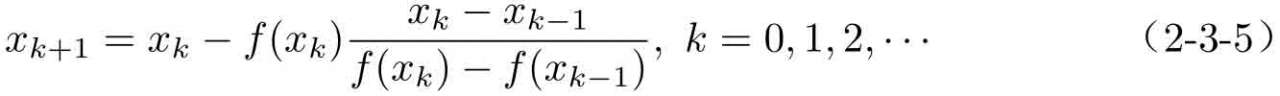
如果采用點運算,則這里的正割函數同樣適用于多元方程的求解。

例2-13 選擇初值x0=10,并求出例2-10中一元超越方程的一個根。
解 先由符號運算的方式推導出給定函數的一階導數。
>> syms x; f=exp(-0.2*x)*sin(3*x+2)+cos(x), diff(f)
可以得出函數的導數為
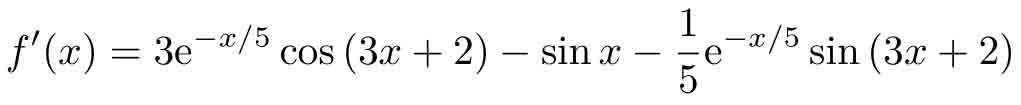
有了函數及其導數,則可以用匿名函數表示它們,再設定搜索的初值為x0=10,這時調用Newton–Raphson求解算法,則可以得出方程的解搜索的中間點為[10,10.8809,11.0700,11.0593,11.0593]T,方程的解為x=11.0593,將其代入原方程,則可以得出誤差為?5.1348×10?16。可以看出,利用這樣的方法求解精度還是比較高的。整個求解過程的示意圖如圖2-9所示,可以看出經過幾步迭代就可以得出方程的解。
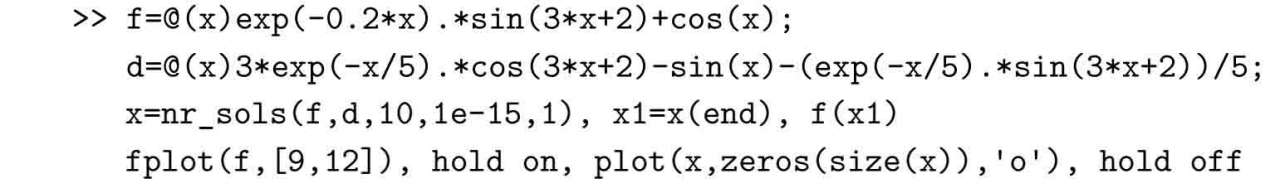
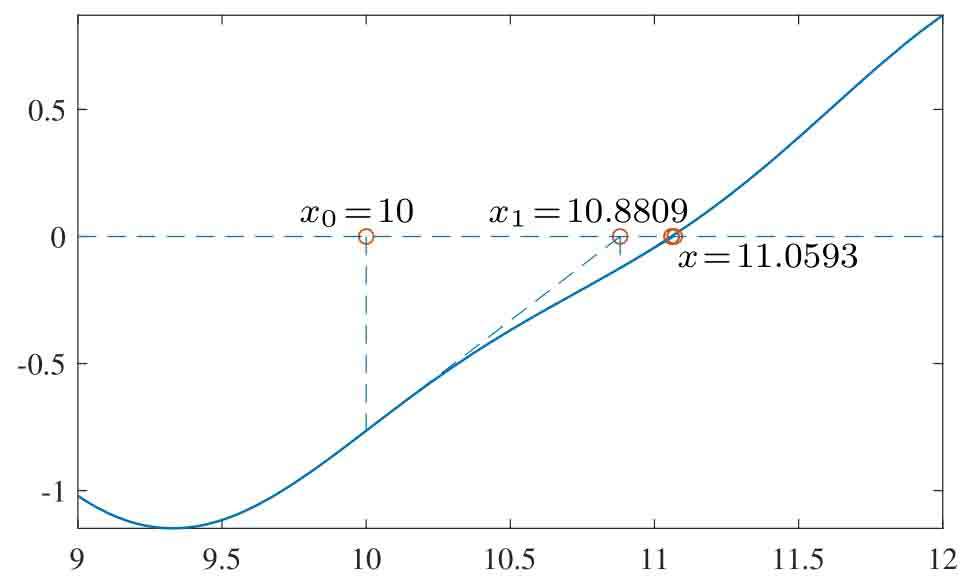
圖2-9 一元方程求解的中間過程
例2-14 試用正割法重新求解例2-13中方程的一個根。
解 選擇兩個初始點x0=9,x1=10,調用求解函數則可以得出求解過程的中間結果為x=[9,10,12.9816,11.3635,10.7250,11.0222,11.0633,11.0592,11.0593,11.0593],其中搜索過程如圖2-10所示。可以看出,雖然這里給出的求解函數效率不如Newton–Raphson算法,但其優勢是無須用戶提供函數的導函數,所以該算法是有意義的。
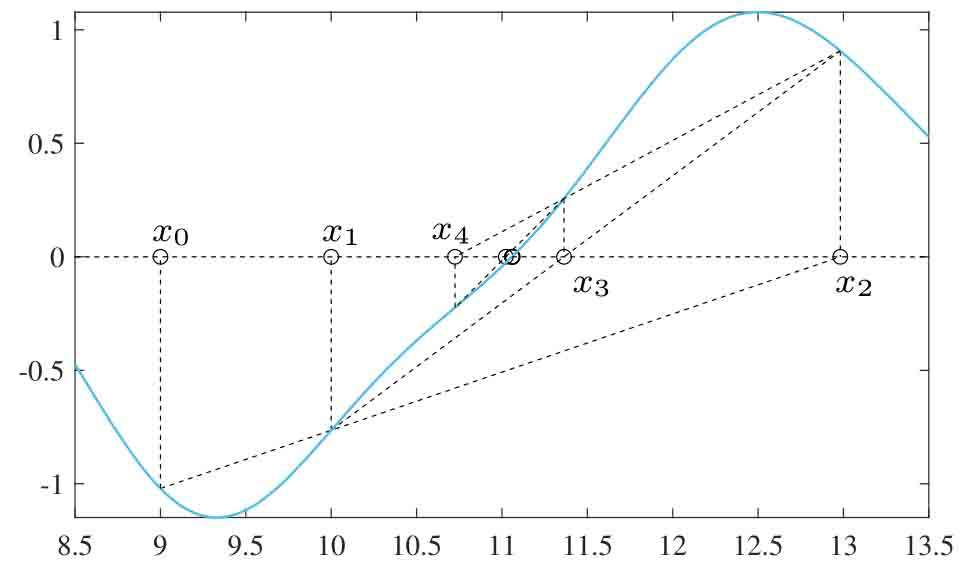
圖2-10 一元方程求解的中間過程
例2-15 試求解例2-11中的二元方程,以(1,1)點為初值搜索到一個解。
解 由于同時含有自變量x和y,這樣的方程是不能直接求解的,需要將其改寫成x的方程,最簡單的方法是令x1=x,x2=y,這樣,原始的方程可以改寫成
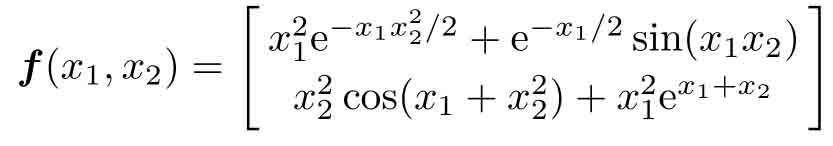
Jacobi矩陣不易用手工的方法推導出來,是需要通過解析推導求解的,所以應該在符號運算框架下輸入原始函數,并通過jacobian()函數計算出該矩陣。
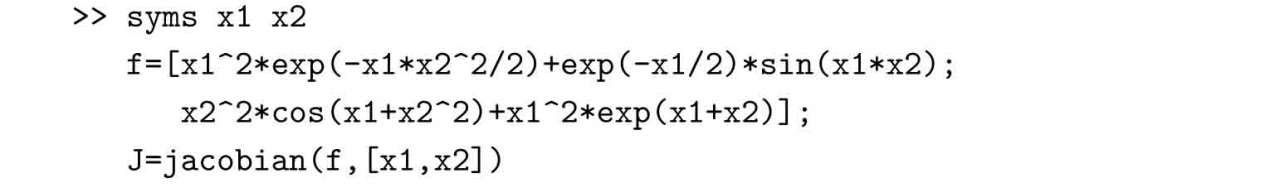
可以推導出函數的Jacobi矩陣為
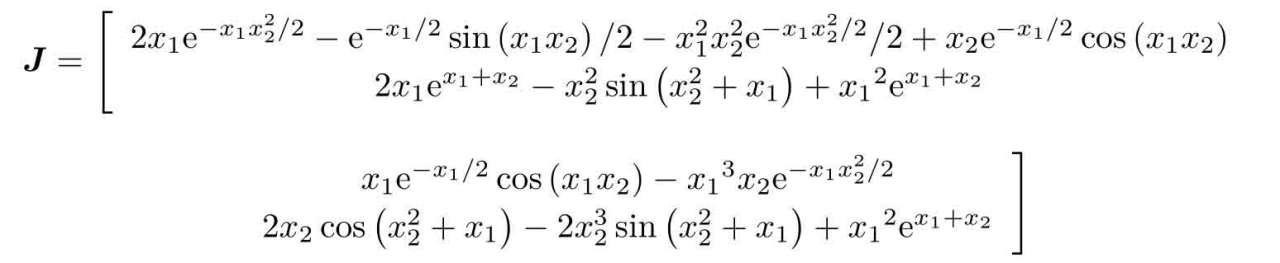
有了原函數與Jacobi矩陣,則可以手工寫出這兩個函數的匿名函數,然后調用基于Newton–Raphson算法的求解函數。

由該初值點出發得出的方程的解為x=[5.1236,?12.2632]T,中間點的個數為18。代入原方程后得出的誤差矩陣范數為3.9323×10?12。從求解的結果看,確實通過該函數可以求出方程的一個根,不過從實際操作看,這樣的方法未免過于復雜,由于需要推導Jacobi矩陣,并將其矩陣用匿名函數的形式手工表示出來,該過程比較容易出錯。
若采用正割方法,則可以給出下面的語句,得出方程的根為x=[1.0825,?1.1737]T,代入方程得出誤差為2.2841×10?14。
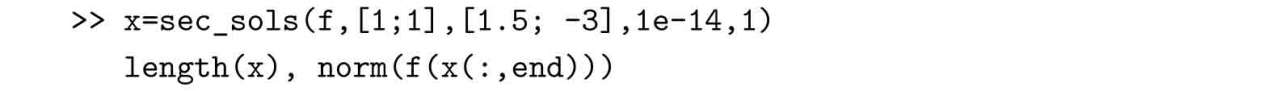
雖然這時函數調用無須用戶提供Jacobi矩陣,但所需的迭代步數為265,求解效率較低,所以對代數方程求解問題而言,需要更好的方法。
2.3.2 MATLAB的直接求解函數
由于上面給出的求解算法比較麻煩,需要提供的信息又比較難獲取,所以在實際方程求解中應該考慮采用更好的方法。MATLAB提供了更實用的求解函數fsolve(),無須提供Jacobi矩陣的句柄,只需給出方程函數的句柄和初值,則可以直接求解任意復雜的非線性方程組,由給出的初值搜索出方程的一個根。該函數的調用格式為
x=fsolve(f,x0)
式中,f為方程函數的句柄;x0為初始向量或矩陣;f函數的維數與x0完全一致,正常情況下得出的x為方程的數值解。
該函數可以至多返回四個變量,這時完整的調用格式為
[x,F,flag,out]=fsolve(f,x0,opts)
式中,x為方程的解;F為x處方程函數的值矩陣;flag如果為正說明求解成功,out變量還將返回一些中間信息。用戶還可以增加輸入選項opts控制求解的算法與精度,后面將通過例子演示。
例2-16 試利用這里介紹的求解函數直接求解例2-15中的方程。
解 仍然可以使用匿名函數描述原始的方程,且無須提供Jacobi矩陣的函數句柄,直接調用求解函數即可以得出方程的解為x1=[0,2.1708]T,將解代入方程則得出誤差向量的范數為3.2618×10?14。雖然這樣得出的解不是例2-15中得出的解,但也是方程的一個解。此外,還可以看出,迭代步數為14次,f函數的調用次數為38,與例2-15中的結果相仿。不過該函數的優勢是無須用戶提供方程的導函數,使用該函數更適合于實際應用,建議采用該方法直接求解方程。
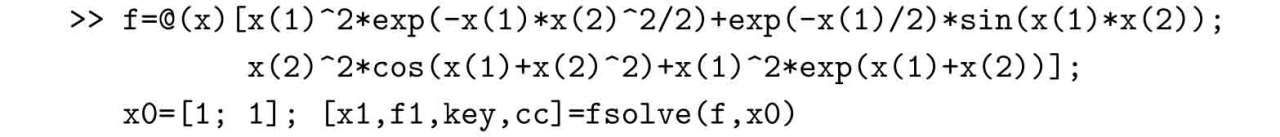
如果將初值修改為x0=[2,1]T,則搜索到的解為x1=[?0.7038,1.6617]T,該解對應的誤差為f1=2.0242×10?12。
>> x0=[2; 1]; x1=fsolve(f,x0), f1=norm(f(x1))
與前面介紹的Newton–Raphson迭代法相比,求解方程的過程已經極大地簡化了,由于只需描述方程本身,無須描述更復雜的Jacobi矩陣,使得方程的求解變得輕而易舉,所以在實際方程求解問題中可以放心使用這樣的方法。
在前面的例子中,未知自變量x與方程函數f(x)都是同維數的向量,編寫出匿名函數就可以描述方程函數,就可以求解方程從而得出方程的解。如果方程f(x)=0中,x與f為同維數的矩陣,也可以直接利用fsolve()函數搜索出方程的數值解。下面以Riccati方程為例介紹矩陣型方程的求解方法。
定義2-8 Riccati代數方程的數學形式為
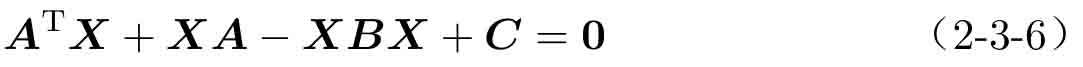
式中,每個矩陣都是n×n矩陣。
Riccati方程是以意大利數學家Jacopo Francesco Riccati(1676?1754)命名的,本意是對應于一類一階微分方程,其原型要求B為正定矩陣,C為對稱矩陣。后來因為微分方程難以求解,所以將其簡化成上面的Riccati代數方程。
從數學角度看,這幾個矩陣可以為任意矩陣。在控制科學領域,可以考慮采用控制系統工具箱提供的are()函數直接求取方程的數值解,不過該函數只能求出Riccati方程的一個根。如果想獲得方程全部的根,則可以考慮調用vpasolve()函數直接求解。下面將給出例子演示Riccati方程與多項式矩陣方程的方法。
例2-17 試求解下面的Riccati代數方程。
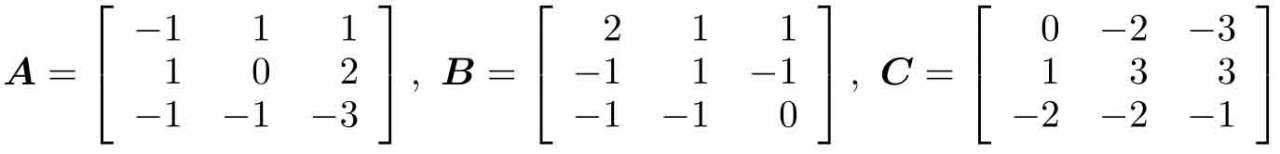
解 可以先輸入這幾個矩陣,然后調用控制系統工具箱中的are()函數求解Riccati方程,并計算得出的誤差矩陣范數。

由控制系統工具箱的are()函數可以直接得出方程的一個根如下,代入原方程可見,該解導致的誤差為1.3980×10?14,說明該解的精度是比較高的。

由于該方程是二次型方程,人們很自然就可以想到,該方程可能有多個根,如何求出其他的根呢?顯然可以嘗試選擇一個不同的初始矩陣,例如幺矩陣,從該矩陣求解方程的根。
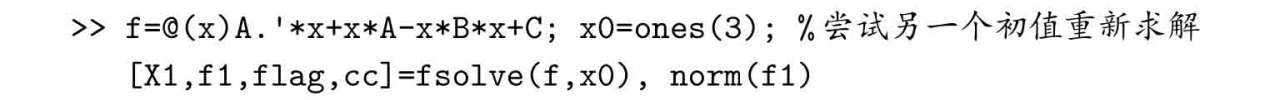
得出方程的解如下,對應的誤差為6.3513×10?9。

顯然,這時得出的解與are()函數得出的解是不一致的。該函數返回的f1矩陣就是方程解處的函數值,即f(X1)。另外,在這個例子中返回的flag值為1,因為它為正數,所以表示求解成功。另外返回的cc信息包括如下內容,表明迭代步數為11,函數調用次數為102,說明求解效率還是很高的。

2.3.3 求解精度的設置
從上面例子得出的解看,誤差偏大。有沒有什么辦法控制誤差的大小呢?
前面在定理2-3中描述了一般迭代方法收斂的條件,給出了兩個誤差限ε1和ε2,這樣的參數是可以人為設定的。可以由opts=optimset命令得出方程求解的控制選項opts,該變量是一個結構體型的數據,其中很多成員變量是可以修改的,例如,AbsTol是絕對誤差限,與前面介紹的常數ε1是一致的,更常用的是相對誤差限RelTol,另外,函數值誤差限FunTol與常數ε2是一致的,所以可以通過設置這些誤差限來控制求解的精度。
除了這兩個選項之外,迭代步數MaxIter和方程函數調用次數MaxFunEvals也經常需要重新設置,否則,在求解方程過程完成之后可能會給出提示,指明求解次數超限。在這種情況下,一方面可以將這兩個選項設置為更大的值,另一方面,也可以將得出的結果作為初值,重新調用fsolve()函數繼續求解,直至找出方程的解為止。這樣的方法還可以與循環結構配合使用。
下面將通過例子演示求解精度的設定與控制方法。
例2-18 試選擇幺矩陣作初值,重新求解例2-17中的Riccati代數方程。
解 如果重新設置求解精度控制選項ff,在調用語句中可以直接使用該控制變量,得出更精確的解,這時,誤差矩陣的范數為2.5020×10?15,比默認精度有了明顯的提高。
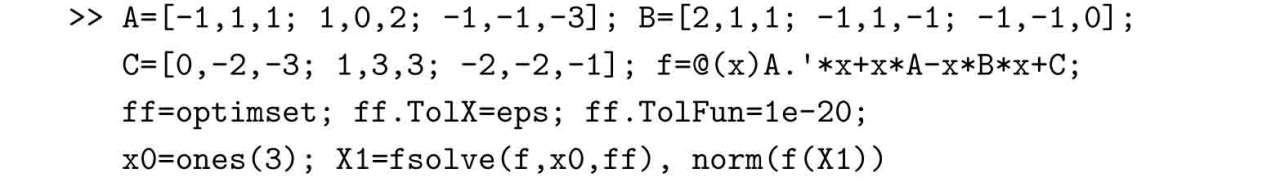
例2-19 試求解下面的Riccati代數方程。
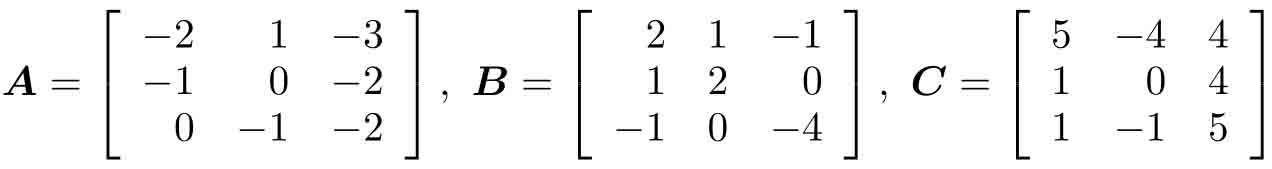
解 由下面的語句可以嘗試求解Riccati方程。
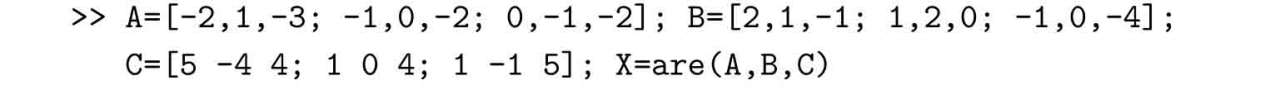
不過求解過程中會得出“No solution:(A,B)may be uncontrollable or no solution exists”((A,B)可能不可控或方程無解)錯誤信息。盡管are()函數失效,仍然可以嘗試求解原方程的數值解方法。例如,可以由下面的語句直接求解。
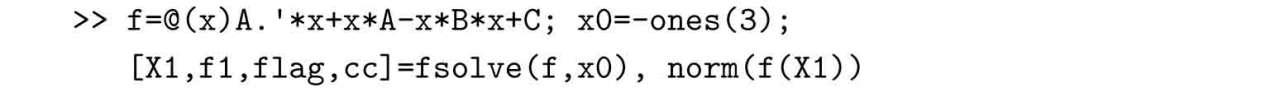
得出的一個解如下,該解的誤差范數為1.2515×10?14。
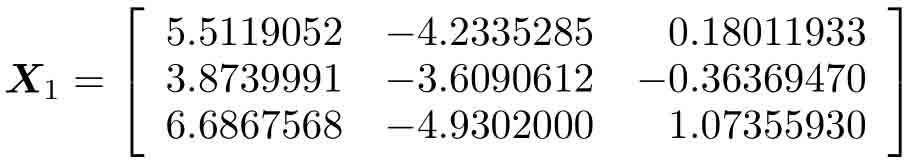
2.3.4 方程的復域求解
使用fsolve()的另一個優勢是,當初值選作復數時,有可能得出方程的復數根。另外,該函數還可以求取復數系數方程的數值解。
例2-20 試求例2-17方程的復數根。
解 如果選擇復數初值,則也有可能得出方程的復數根,同時可以驗證,該根的共軛復數矩陣也滿足原始方程。

由該初值可以搜索出的解如下,相應的誤差為1.1928×10?14。對這個例子還可以同步求出方程根的共軛矩陣,經檢驗該矩陣也滿足于原方程。
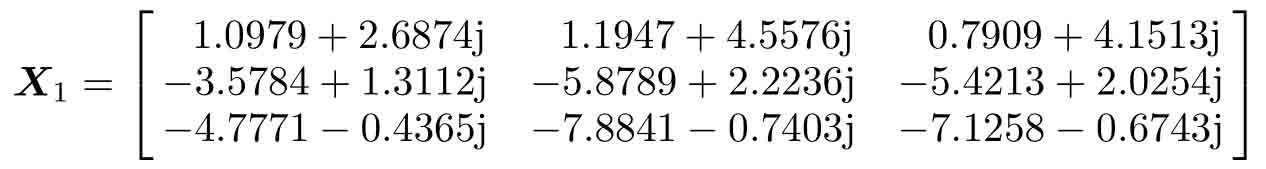
對這個具體問題而言,如果初始值選擇成實部為幺矩陣,虛部為單位陣的矩陣,則搜索出的將是實數解,這也說明由復數初始搜索點出發也能搜索出實數根。不過值得注意的是,這樣搜索出的結果可能帶有微小的虛部,其范數在該例子中為6.4366×10?19,應該由real()函數提取出來。

例2-21 如果Riccati代數方程的系數矩陣A變成復數矩陣,試重新求解該方程。
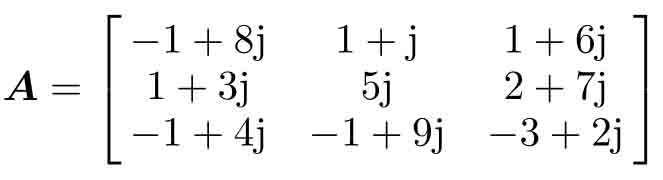
解 可以將各個矩陣輸入到MATLAB的工作空間,然后使用匿名函數描述原方程。注意,原方程使用的是矩陣A的直接轉置AT,不是Hermite轉置AH,所以在匿名函數中應該使用A.',而不能使用A',否則方程描述是錯誤的,求解就沒有意義了。可以使用下面命令直接求解并檢驗原方程,并求出解的共軛復數矩陣。

這樣可以得出方程的解為
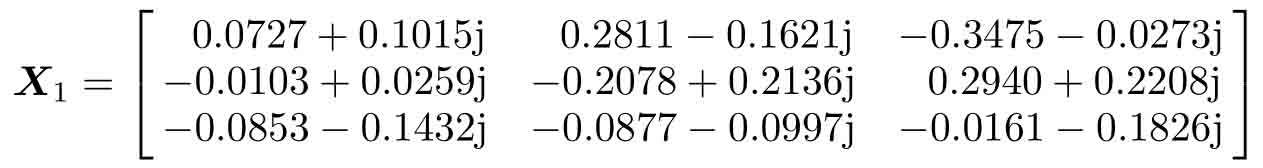
如果將解代入原方程,則得出誤差矩陣的范數為5.4565×10?13。對這個特定的例子而言,即使使用實數起始搜索矩陣,也能搜索出方程的復數解。此外,雖然能直接求出解矩陣的共軛復數矩陣,但顯然該矩陣不滿足原方程,這與實數矩陣方程不同,因為在實數矩陣方程中,如果找到了方程的一個解,其共軛矩陣一般會滿足原方程。
如果采用MATLAB控制系統工具箱的are()函數求解方程的解:
>> X=are(A,B,C), norm(f(X))
得出矩陣方程的解如下,在求解過程中也沒有任何警告或錯誤信息,不過試圖將該解代入原方程后得出的誤差過大,為10.5210,說明得出的解根本不滿足原始方程。
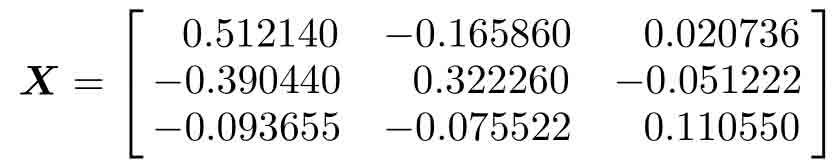
- C語言程序設計實踐教程(第2版)
- 數據庫程序員面試筆試真題與解析
- ReSharper Essentials
- 秒懂設計模式
- 你必須知道的204個Visual C++開發問題
- SAP BusinessObjects Dashboards 4.1 Cookbook
- Spring快速入門
- 移動互聯網軟件開發實驗指導
- Unity 3D/2D移動開發實戰教程
- Spring Boot+Vue全棧開發實戰
- Elasticsearch Essentials
- Unity Android Game Development by Example Beginner's Guide
- Java程序設計教程
- Drupal Search Engine Optimization
- Java程序設計實用教程(第2版)