2.9 表針的對調問題

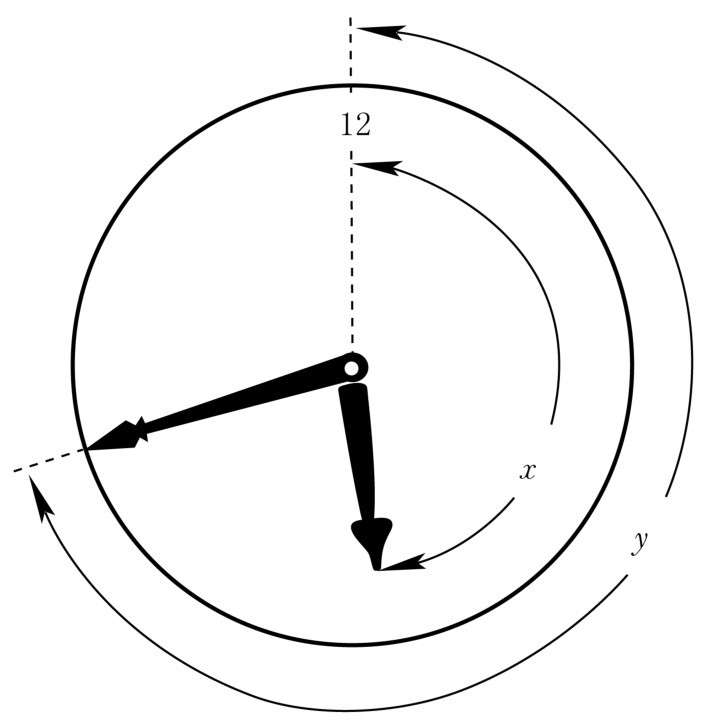
[題] 著名物理學家愛因斯坦生病的時候，為了逗他開心，他的一個做傳記作者的朋友莫希柯夫斯基給他出了下面這道題（圖2-3）：

“假設表針的初始位置是在12點。在這個位置，如果把較長的分針和較短的時針對調一下，它們所指示的時間還是存在的。但是在很多別的時候，把兩針對調之后所出現的結果就不合理了，比如6點的時候，我們如果把兩針對調，出現的結果就是正常情況下不可能出現的：這個時候時針指向12而分針指向6。這種位置關系是不合理的。由此可以引出這樣一個問題：表針處在什么位置的時候，即使兩針對調，所得的新位置顯示的仍然是可能存在的時間？”

愛因斯坦回答道：“非常好，這個問題十分有趣而且也不是特別簡單，非常適合躺在病床上的人。只是對于我來說，它恐怕消磨不了多少時間，我已經快解出來了。”

愛因斯坦從床上坐起來，用幾筆在紙上勾出了一個草圖來表示問題的條件。他解這個問題所用的時間甚至不超過莫希柯夫斯基敘述這個問題所用的時間……

那么，他是怎樣解答這道題的呢？

[解] 首先，我們不妨把表盤圓周分成相等的60份，并以每份為單位，來計算表針從12開始所走的距離。

假設在時針從12起走了x個刻度，分針走了y個刻度之后，達到了符合題目要求的位置。時針走過60個刻度需要12個小時，這也就是說，時針每小時能走5個刻度，那么它走過x個刻度所需的時間就是小時。換句話說，就是在表走到12點之后，又過了小時。每個小時有60分鐘，所以分針走過y個刻度所用的時間就是小時。也就是說，分針是在小時之前經過數字12的。換言之，兩根指針在12的地方重合之后又過了小時。由于這個數所表示的是12點之后又過去了幾個整小時，所以這個數是從0到11之間的一個整數。

當兩根指針的位置調換了之后，我們可以用同樣的方法求出從12點到調換后的時間為小時。這個數也是個從0到11之間的整數。

根據這些，我們可以列出聯立方程：

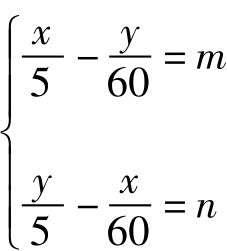
由這個聯立方程我們可以解出：

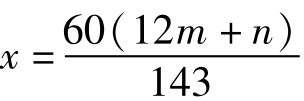
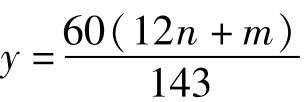
在這個方程中，m和n都可以任取從0到11之間的整數。所以，要想確定全部所求表針的位置，只要把從0到11之間的全部整數都代入到上述的方程中就可以了。由于m可以取的12個數中任何一個都可以與n可以取的12個數中的任意一個組合，所以，很多人會覺得這道題應該有12×12=144個解。實際上，不是這樣。由于m、n均為0時與m、n均為11時表針所處的都是同一個位置，也就是12點。所以，這道題其實只有143個解。

我們不討論所有可能出現的情況，只找兩個例子來看一看。

第一例：

當m=1, n=1時，

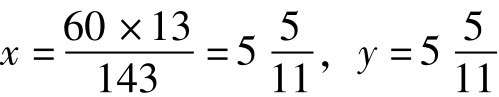
對應的時刻也就是1點分，此時時針和分針是重合在一起的；時針和分針重合在一起的時候，它們當然可以彼此對調。

第二例：

當m=8, n=5時，

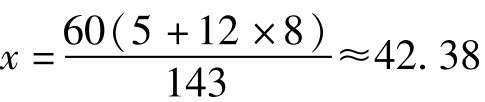
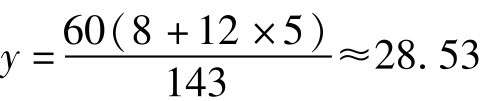
這時所指的時刻應該分別是8點28.53分和5點42.38分。

當我們把表盤的圓周平均分成143份時，所得到的平分點就是這道題的解。表針指向這樣的點時，把時針和分針對調，它們所指的時間仍然存在。而當表針指向這143個點之外的那些點時，如果對調時針和分針，它們所指的時間將會是不合理的。