- 寫給孩子的趣味代數學
- (蘇)雅科夫·伊西達洛維奇·別萊利曼
- 1601字
- 2019-12-27 16:35:40
1.9 計數觸發器
有一種電子裝置叫作觸發器,它主要由兩個電子管組成,這種電子管跟收音機的電子管差不多。當電流流入觸發器中時,它只能從左邊的電子管或者右邊的電子管中通過,也就是說,它只能通過一個電子管。觸發器一共有四個觸點,其中兩個是用來從外部接收一種叫作脈沖的短暫電信號的;而另外兩個則是用來從觸發器輸出回答脈沖的。接收到外部輸入脈沖的瞬間,觸發器會改變狀態,發生“翻轉”,這時,原來導通的電子管變成閉合狀態,電流轉而從另外一個電子管流過。在右邊的電子管閉合,左邊的電子管導通的瞬間,觸發器就會從接觸點輸出回答脈沖。
當右邊的電子管閉合時,我們規定觸發器的狀態為“狀態0”;當右邊的電子管導通時,我們規定觸發器的狀態為“狀態1”。那么在連續給觸發器輸入幾個脈沖后,觸發器是怎樣工作的呢?
假設一開始左邊的電子管是導通的,即觸發器的初始狀態是狀態0(圖1-1)。輸入第一個脈沖后,左邊的電子管將會變為閉合狀態,即觸發器翻轉成狀態1。這時,觸發器不輸出回答脈沖。輸入第二個脈沖后,左邊的電子管導通,觸發器重新回到狀態0。這時觸發器輸出回答脈沖。
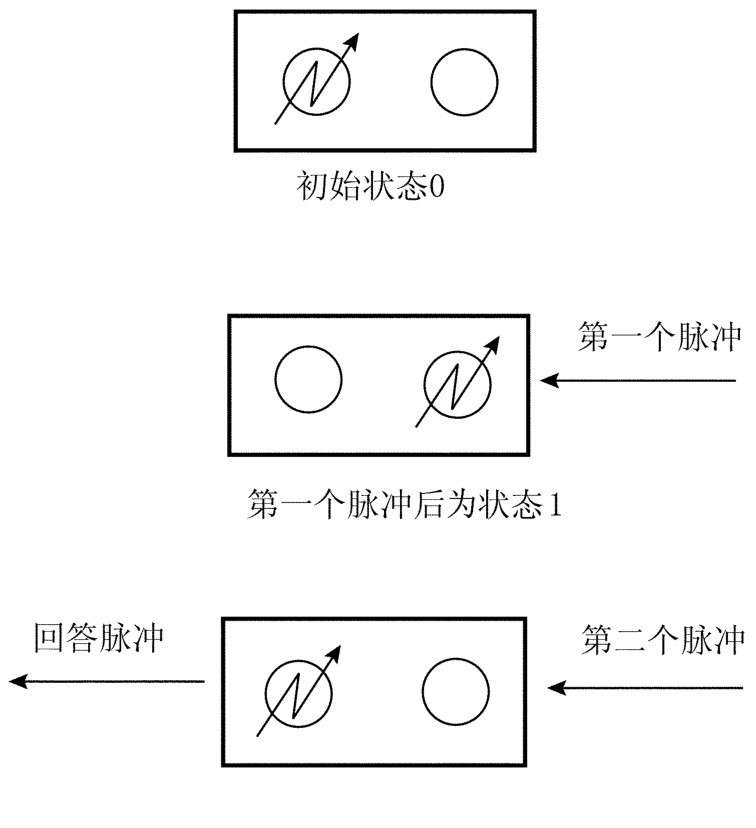
圖1-1
觸發器在經過兩個脈沖之后,又回到初始狀態0。繼續輸入第三個脈沖和第四個脈沖的情況跟第一個脈沖和第二個脈沖一樣。后面都是如此循環往復的。也就是說,每輸入兩個脈沖,觸發器就會輸出一次回答脈沖。
現在我們假設有好幾個觸發器,給第一個觸發器輸入脈沖信號,然后把第一個觸發器輸出的回答脈沖加到第二個觸發器上,第二個觸發器輸出的回答脈沖加到第三個觸發器上,按照圖1-2的順序依次連接,之后,我們來看一下這幾個觸發器是怎樣工作的。

圖1-2
假設一共有5個觸發器,將它們的初始狀態都設為0,那么初始時的組合就是00000。現在,對這組觸發器加第一個脈沖,這時,第一個觸發器轉變為狀態1。由于此時第一個觸發器沒有輸出回答脈沖,所以,其他觸發器仍然處在狀態0。此時這一組觸發器形成的組合就是00001。在第二個脈沖之后,第一個觸發器發生翻轉,變回狀態0,它發出的回答脈沖接通第二個觸發器,第二個觸發器變為狀態1,其余的觸發器依然處于狀態0。這時,觸發器的組合就變成了00010。接著第一個觸發器又接收到了第三個脈沖,這時它變為狀態1,由于沒有輸出回答脈沖,其余的觸發器狀態不變,這時的組合就是00011。在第四個脈沖后,第一個觸發器翻轉,并輸出回答脈沖,第二個觸發器由于第一個觸發器的脈沖作用也發生翻轉,并輸出回答脈沖,第三個觸發器因此被接通并發生翻轉,變為狀態1,此時的組合就是00100。
按照這樣一直進行下去,可以得到以下結果:
第一個脈沖 組合00001
第二個脈沖 組合00010
第三個脈沖 組合00011
第四個脈沖 組合00100
第五個脈沖 組合00101
第六個脈沖 組合00110
第七個脈沖 組合00111
第八個脈沖 組合01000
……
在二進制計數法中,所有的數都用0和1表示,與十進制不同,二進制后一位上的1是前一位上的1的2倍,而不是10倍。將二進制數轉化為十進制數時,只需要從右到左用二進制的每個數去乘以2的相應次方,然后將所得的結果相加就可以了。需要注意的是,次方要從0開始,從右到左每次增加1。例如,二進制數10011轉化為十進制數就是1×20+1×21+0×22+0×23+1×24=1+2+16=19。
連接起來的觸發器就是以二進制計數法“記錄”了從外面輸入的脈沖的次數。需要注意的是,觸發器每翻轉一次,就會記錄一個輸入進來的脈沖,而這整個過程所需要的時間不過一億分之幾秒!現在的計數觸發器每秒能夠“計算”出1000多萬個脈沖。一般來說,我們的眼睛最快只能來得及識別每隔0.1秒出現一次的信號,所以計數觸發器的速度大約是人眼識別速度的100萬倍。
假如把20個觸發器按照以上方法連接在一起,那么它就能記錄不超過二進制的20位的數目的輸入信號。也就是說,它可以“計數”到(220-1),這個數字大于100萬。而當我們把64個觸發器連在一起時,我們就可以利用它來記錄著名的“象棋數字”了。
高速計數對于核物理的實驗研究有著十分重大的意義。比如原子裂變時釋放出來的各種粒子的數目就可以用這種方法來計算。