第6章　利率的風險結構與期限結構[視頻講解]

6.1　復習筆記

1．利率的風險結構

利率的風險結構是指期限相同的各種債券或貸款在違約風險、流動性和所得稅規定等因素作用下各不相同的利率間的關系。利率的風險主要包括以下幾個方面：

（1）違約風險

①違約風險與風險溢價

違約風險（default risk）是指債券發行人違約的可能，也就是指，無力支付利息或在債券到期時無法償還本金所導致的風險。一般認為國債沒有違約風險，像這種不存在違約風險的債券稱為無違約風險債券。

風險溢價（risk premium）指的是具有違約風險債券的利率和無違約風險債券利率之間的差額，是人們因為持有某種風險債券必須獲得的額外利息。

②違約風險對利率的影響

無違約風險債券（國債）和公司長期債券市場的供給需求如圖6-1所示。假設公司債券最初也屬于無違約風險債券，且兩種債券屬性相同（風險與期限相同），它們的初始均衡價格和利率水平是相等的P^C₁=P^T₁=i^T₂，此時，公司債券的風險溢價為零。

如果公司開始蒙受巨額損失，公司違約的可能將會增大，導致公司債券違約風險上升，從而這些債券的預期收益率將會下降。而且，公司債券收益率的不確定性也會上升。根據資產需求理論，由于公司債券相對于無違約風險的國債預期收益率下降，同時其相對風險也上升，公司債券受歡迎程度會下降（在其他條件不變的情況下），其需求量也會下降，圖6-1（a）中的公司債券需求曲線將會從D^C₁左移到D^C₂。

同時，無違約風險的國債相對于公司債券預期收益率上升，且其相對風險下降，國債將會更受歡迎，其需求量上升，如圖6-1（b）所示，其需求曲線從D^T₁右移到D ^T₂。

如圖6-1所示，公司債券的均衡價格（左縱軸）從P^C₁下降到P^C₂，而利率與債券價格負相關，公司債券的均衡利率（右縱軸）從i^C₁上升到i^C₂。同時，國債的均衡價格從P^T₁上升到P^T₂，其均衡利率由i^T₁下降到i^T₂。公司債券和無違約風險債券的利率差距——也就是公司債券的風險溢價——從零上升為i^C₂-i^T₂。由此可以得出如下結論：具有違約風險的債券總是存在正的利率溢價，其違約風險的上升將導致風險溢價隨之上升。

（2）流動性

流動性資產是指能以較低成本迅速轉化為現金的資產。資產流動性越強，它的受歡迎程度也就越高（在其他條件不變的情況下）。政府長期債券是流動性最高的長期債券，公司債券的流動性要差一些。

如圖6-1所示，可以運用供給與需求分析來說明：如果公司債券相對于國債流動性降低，將會導致兩種債券的利差變大。首先，假設初始公司債券和國債流動性相同，所有其他屬性也都是一樣的。如圖6-1所示，其初始均衡價格與均衡利率都相等：P^C₁=P^T₁，i^C₁=i^T₁。如果由于其交易范圍變小，公司債券相對于國債流動性下降，根據資產需求理論，公司債券需求量下降，推動其需求曲線從D^C₁左移 到D^C₂，如圖（a）所示；此時與公司債券相比，國債流動性相對提高，其需求曲線從D^T₁右移至D^T₂，如圖（b）所示。圖6-2中曲線的移動最終表明流動性較差的公司債券價格下降，利率上升；流動性較好的國債價格上升，利率下降。

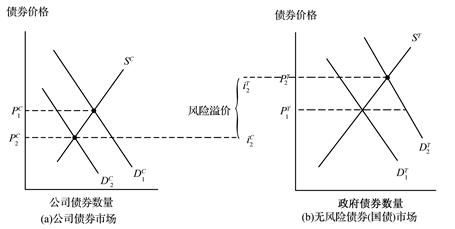
圖6-1　公司債券違約風險上升的影響

最終結果是，兩種債券之間的利差上升。因此，公司債券利率與國債利率之間的差額（也就是風險溢價）不僅反映了公司債券的違約風險，同時也反映了其流動性風險。這就是有時將風險溢價稱為流動性溢價的原因。更準確地說應將其稱為“風險與流動性溢價”，但為了方便通常將其稱為“風險溢價”。

（3）所得稅因素

債券持有人真正關心的是稅后的實際利率，因此，如果債券利息收入的稅收待遇視債券的種類不同而存在差異，這種差異就必然要反映到稅前利率上來。稅率越高的債券，其稅前利率也應該越高。這可以用以下兩種方法說明：

①數理推導。假定有債券A和債券B，它們的違約風險和流動性均相同，但是債券A利息收入的所得稅率為t_A，而債券B利息收入的所得稅率為t_B。那么，債券A的稅后利率就等于i_A（1-t_A），債券B的稅后利率就等于i_B（1-t_B），其中i_A，i_B分別為債券A和債券B的稅前利率。因此，要使這兩種債券的稅后利率相等，就必須有

i_A=i_B（1-t_B）/（1-t_A）

從上式中可以清楚地看出，稅率越高的債券，其稅前利率也應該越高。

②圖形分析。運用圖6-2中所示的供給需求分析來理解為何低稅率債券利率低于高稅率債券的利率。假設在初始條件下低稅率債券和高稅率債券具有相同的特征，因此，如圖所示，其債券價格與利率相等：P^m₁=P^T₁，i^m₁=i^T₁。一旦引入低稅率債券的稅收優勢以后，其相對于高稅率債券的稅后預期收益率將會上升，低稅率債券更受歡迎，需求量上升，其需求曲線從D^m₁右移到D^m₂。結果，其均衡價格從P^m₁上升到P^m₂，均衡利率從i^m₁下降到i^m₂。相反，相對于低稅率債券，高稅率債券受歡迎程度下降，其需求量降低，其需求曲線從D^T₁左移到D^T₂其均衡價格從P^T₁下降到P^T₂，均衡利率從i^T₁上升到i^T₂。最后的結果是低稅率債券利率下降，高稅率債券利率上升，這解釋了為什么低稅率債券的利率低于高稅率債券的利率。

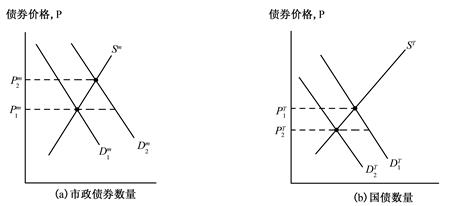
圖6-2　市政債券和國債的利率

（4）小結

利率的風險結構（具有相同期限債券利率之間的關系）可以由三個因素解釋：違約風險、流動性和債券利息收入的所得稅待遇。債券的風險溢價（債券利率與無違約風險的國債利率之間的差額）隨著債券違約風險的上升而上升。國債的高流動性特征也解釋了為何其利率要比流動性相對較差的債券利率要低。如果某種債券具有某種優惠的稅收待遇，其利率也會降低。

2．利率的期限結構

（1）利率的期限結構與收益率曲線

利率的期限結構是指其他特征相同而期限不同的各種債券利率之間的關系。

將期限不同，但風險、流動性和稅收特征都相同的債券的收益率連成一條曲線，稱為收益率曲線，它描述了某些類型債券（如政府債券）利率的期限結構。收益率曲線可以分為向上傾斜、水平以及向下傾斜三種（最后一種通常被稱作反向收益率曲線）。收益率曲線向上傾斜表明長期利率高于短期利率，收益率曲線呈水平形狀表示長期利率等于短期利率，收益率曲線向下傾斜表明長期利率低于短期利率。收益率曲線可以有更復雜的形狀，它可以先向上傾斜后向下傾斜或相反。

圖6-3　收益率曲線

利率期限結構理論除了要解釋收益率曲線在不同時期具有不同形狀之外，還必須解釋以下經驗事實：

①不同期限債券的利率隨時間一起變動；

②如果短期利率較低，收益率曲線更有可能向上傾斜，如果短期利率較高，收益率曲線更有可能向下傾斜；

③收益率曲線幾乎總是向上傾斜的。

人們提出了用于解釋利率期限結構的三個理論，即：預期理論、分割市場理論、流動性溢價理論。預期理論能夠較好地解釋我們列出的3個事實中的前兩個，但不包括③。分割市場理論能很好地解釋事實③，但不包括預期理論能夠較好地解釋其他兩個事實。由于都能解釋對方所不能圓滿解釋的事實，為了更好地理解利率的期限結構，把兩種理論的特點結合起來，這樣就出現了流動性溢價理論，它可以較好地解釋全部3個事實。

（2）預期理論

基本命題：長期債券利率等于長期債券到期之前人們預期的短期利率的平均值。

前提假設：①投資者對債券的期限沒有偏好，其行為取決于預期收益的變動。如果一種債券的預期收益低于另一種債券，那么，投資者將會選擇購買后者。②所有市場參與者都有相同的預期。③在投資人的資產組合中，期限不同的債券是完全替代的。④金融市場是完全競爭的。⑤完全替代的債券具有相等的預期收益率。

理論推導：假定某投資人面臨下列兩個不同的投資決策：

決策A：在第t期購買一份利率為i_t的一期債券，到期以后再購買另一份一期債券，第t+1期的預期利率水平為i^e_t+1。

決策B：在第t期購買利率為i_2t的兩期債券。

則前一種策略的預期收益率為（1+i_t）（1+i^e_t-1）-1；第二種投資策略的預期收益率為（1+i_2t）²-1。由于投資者對債券的期限沒有特殊偏好，所以在均衡的情況下，這兩種投資策略的預期收益率應該相等。所以有：

（1+i_2t）²-1=（1+i_t）（1+i^e_t+1）-1。

即：

2i_2t+i²_2t=i_t+i^e_t+1+i_i·i^e_t+1。

由于i²_2t，i_t·i^e_t+1的值都很小，可以忽略不計，所以由上式就得：i_2t=。

事實上，將模型稍作拓展，便可得出：n期債券的利率i_n等于在其期限內可能出現的n個1期利率的平均數。用公式表示，就是：i_nt=（i_t+i^e_t+1+i^e_t+2+…+i^e_t+（n-1））/n。

理論評價：

預期理論是一種非常精巧的理論，解釋了利率的期限結構（以收益率曲線表示）在不同時期變動的原因。根據預期理論，向上傾斜的收益率曲線意味著短期利率將會上升。如果在當前，長期利率高于短期利率，這表明對未來短期利率預期的平均值比當期短期利率要高，然而這樣的情況只有當短期利率預期上升時才會出現。而向下傾斜的收益率曲線則意味著預期未來短期利率的平均值將低于當期的短期利率，通常這表示未來短期利率預期的平均值將會下降。而根據預期理論，水平的收益率曲線意味著未來短期利率預期的平均值不變。

預期理論能解釋事實①，即不同期限債券的利率隨時間一起變動的情況。在歷史上，短期利率的一個特點是如果今天上升，則未來將趨于更高。可見短期利率的上升將使人們調高對未來短期利率的預期。由于長期利率等于未來短期利率預期的平均值，所以短期利率的上升將使長期利率同樣上升，這就解釋了為什么短期利率和長期利率同時變動。

運用預期理論同樣能解釋事實②，即在短期利率較低時，收益率曲線趨向于向上傾斜；在短期利率較高時，收益率曲線趨向于向下傾斜。這是因為如果短期利率較低，通常人們預測它在未來會升高到正常的水平，而且相對于當期的短期利率，未來短期利率預期的平均值較高。所以長期利率要比當期的短期利率高得多，從而收益率曲線向上傾斜。反之，如果當前短期利率較高，則人們往往預期它將會下降。這樣，未來短期利率預期的平均值較當期的短期利率要低，導致長期利率低于短期利率，即收益率曲線向下傾斜。

之所以說預期理論是一個非常吸引人的理論是因為它對利率期限結構的狀況提供了比較簡單的解釋，然而預期利率并不能解釋事實③，即收益率曲線通常都是向上傾斜的。向上傾斜的收益率曲線意味著預期未來短期利率上升。但事實上，短期利率可能上升也可能下降，因此，根據預期理論，收益率曲線的通常形狀應該是水平的而不是向上傾斜的。

（3）分割市場理論

基本命題：期限不同的證券的市場是完全分離的或獨立的，每一種證券的利率水平在各自的市場上，由對該證券的供給和需求所決定，不受其它不同期限債券預期收益變動的影響。

前提假設：①投資者對不同期限的證券有較強的偏好，因此只關心他所偏好的那種期限的債券的預期收益水平;②在期限相同的證券之間，投資者將根據預期收益水平的高低決定取舍，即投資者是理性的;③理性的投資者對其投資組合的調整有一定的局限性，許多客觀因素使這種調整滯后于預期收益水平的變動;④期限不同的證券不是完全替代的。這一假定和預期假說的假定正好截然相反。

理論推導：一般而言，持有期較短的投資人寧愿持有短期證券，而持有期較長的投資人可能傾向于持有長期證券。由于投資人對特定持有期的證券具有特殊的偏好，因而可以把證券的不同期限搭配起來，使它等于期望的持有期，從而可以獲得確定的無風險收益。不同期限債券的需求與供給差異決定了收益率曲線的不同形狀。

理論評價：

平均看來，大多數人通常更愿意持有利率風險較低的短期債券，這樣分割市場理論就能解釋事實③，即收益率曲線通常向上傾斜。這是因為在通常的情況下，長期債券的需求低于短期債券的需求，造成長期債券價格相對較低，而利率相對較高，因此收益率曲線通常向上傾斜。

盡管分割市場理論不能對事實①和事實②作出解釋。由于它將不同期限的債券市場視作是完全分割的，一種期限債券利率上升就不會對另一種債券的利率產生影響。因此，它無法解釋具有不同期限債券的利率隨時間一起變動的事實（事實①）。其次，該理論對長期債券相對于短期債券的供求如何隨短期的利率水平的變化而變化，沒有給出清楚的答案，它也無法解釋為何短期利率水平較低時，收益率曲線向上傾斜，而短期利率較高時，收益率曲線向下傾斜（事實②）。

（4）流動性溢價理論與期限優先理論

基本命題：長期債券的利率水平等于在整個期限內預計出現的所有短期利率的平均數，再加上由債券供給與需求決定的流動性溢價。

前提假設：①期限不同的債券之間是互相替代的，一種債券的預期收益率確實會影響其他不同期限債券的利率水平；②投資者對不同期限的債券具有不同的偏好，如果某個投資者對某種期限的債券具有特殊偏好，那么，該投資者可能更愿意停留在該債券的市場上，表明他對這種債券具有偏好停留；③投資者的決策依據是債券的預期收益率，而不是他偏好的某種債券的期限；④不同期限債券的預期收益率不會相差太多。因此在大多數情況下，投資人存在喜短厭長的傾向；⑤投資人只有能獲得一個正的時間溢價，才愿意轉而持有長期債券。

理論推導：流動性溢價理論可以寫為：

i_nt=（i_t+i^e_t+1+i^e_t+2+…+i^e_t+（n-1））/n+l_nt

l_nt=時間t上n周期債券的流動性溢價。l_nt總是正值，且隨到期期限n同向變動。

理論評價：

它可以解釋事實①，即不同期限債券利率隨時間一起波動。如果短期利率上升則意味著未來預期短期利率平均值將會上升，根據等式（6.3），長期利率將隨之上升。

該理論同樣能解釋事實②，即當短期利率較低時，收益率曲線陡直地向上傾斜，而短期利率較高時，收益率曲線向下傾斜。這是因為對較低的短期利率，投資者通常預期它會上升到正常水平，因此，相對于當期的短期利率來說，未來短期利率預期的平均值就比較高，在加入正的流動性溢價以后，長期利率將比短期利率高出很多，這也是收益率曲線向上陡直傾斜的原因。反之，對于較高水平的短期利率，人們通常的預計是它會下降到正常水平。這導致人們對未來短期利率預期的平均值比當期的短期利率要低得多，從而使得長期利率水平在短期利率之下，雖然加入了正的流動性溢價，收益率曲線的形狀依然是向下傾斜的。

流動性溢價理論可以解釋事實③，即收益率曲線通常的形狀是向上傾斜的。根據流動性溢價理論，投資者更偏好于短期債券，因此流動性溢價隨著債券期限的拉長而上升，這樣即使對未來短期利率預期的平均值沒有發生改變，長期利率也較短期利率高一些，這就解釋了收益率曲線向上傾斜的事實。

在流動性溢價為正值的情況下，與收益率曲線有時向下傾斜的事實并不矛盾。因為在短期利率預期未來會大幅度下降的情況下，預期的短期利率的平均數即使再加上一個正的時間溢價，長期利率仍然低于現行的短期利率水平。

流動性溢價理論有一個很吸引人的特點：根據該理論，只要通過考察收益率曲線的斜率就可以得知市場對未來短期利率的預測。在圖6-4（a）中所示的陡峭上升的收益率曲線表明在未來短期利率預期將會上升。圖6-4（b）中較為平緩地向上傾斜的收益率曲線表明未來短期利率預期將不會有太大的升降。圖6-4（c）所示的水平的收益率曲線表明未來短期利率預期將有輕微地下降。最后圖6-4（d）所示的向下傾斜的收益率曲線表明未來短期利率預期將急劇下降。

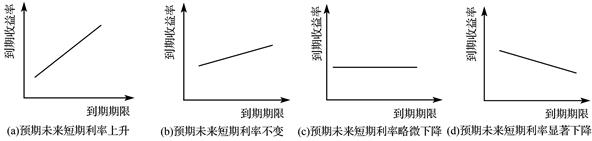
圖6-4　流動性溢價理論中的收益率曲線和未來短期利率的市場預期

（5）小結

流動性溢價理論是關于利率期限結構理論中最被廣泛接受的理論，這是因為它能很好地解釋有關利率期限結構的經驗事實。它綜合了預期理論和分割市場理論的特點，認為長期利率等于流動性溢價與債券到期日之前短期利率預期平均值之和。

流動性溢價理論解釋了如下事實：①具有不同期限的債券的利率隨時間一起變動。②如果短期利率較低，收益率曲線更可能向上傾斜；如果短期利率較高，收益率曲線更可能向下傾斜。③收益率曲線幾乎總是向上傾斜。

這種理論還能幫助我們預測未來短期利率的走勢。陡峭上升的收益率曲線意味著短期利率預期上升，平緩上升的收益率曲線意味著短期利率預期保持不變，水平的收益率曲線意味著短期利率預期輕微下降，而向下傾斜的收益率曲線意味著短期利率預期大幅下降。